Để kiểm tra học kì II, môn Toán – lớp 7 trường THCS Cửa Nam

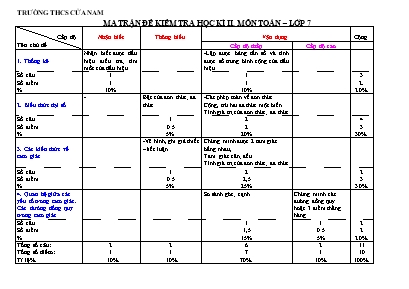
TRƯỜNG THCS CỬA NAM
MA TRẬN ĐỂ KIỂM TRA HỌC KÌ II, MÔN TOÁN – LỚP 7
 Cấp độ
Tên chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Thống kê
Nhận biết được dấu hiệu điều tra; tìm mốt của dấu hiệu
-Lập được bảng tần số và tính được số trung bình cộng của dấu hiệu
Số câu
Số điểm
%
1
1
10%
1
1
10%
3
2.
20%
2. Biểu thức đại số
-
Bậc của đơn thức; đa thức
-Các phép toán về đơn thức
Cộng, trừ hai đa thức một biến 
Tính giá trị của đơn thức; đa thức
Số câu
Số điểm
%
1
0.5
5%
2
2
20%
4
3
30%
3. Các kiến thức về tam giác
-Vẽ hình, ghi giả thiết – kết luận
Chứng minh được 2 tam giác bằng nhau, 
Tam giác cân; đều
Tính giá trị của đơn thức; đa thức
Số câu
Số điểm
%
1
0.5
5%
2
2,5
25%
2
3
30%
4. Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
So sánh góc; cạnh
Chứng minh các đường đồng quy hoặc 3 điểm thẳng hàng
Số câu
Số điểm
%
1
1,5
15%
1
0.5
5%
2
2
20%
Tổng số câu:
Tổng số điểm:
Tỉ lệ%
2
1
 10%
2
1
 10%
6
7
70%
2
1
10%
11
10
100%
TRƯỜNG THCS CỬA NAM
ĐỀ KIỂM TRA HỌC KÌ II, MÔN TOÁN – LỚP 7
Thời gian: 90 phút
Câu 1: (2 điểm)	
	Điểm kiểm tra một tiết môn Toán của 30 học sinh lớp 7A được ghi lại trong bảng sau:
7
9
1
2
10
10
5
4
5
5
7
9
7
10
2
5
5
4
5
8
7
7
9
9
2
5
4
4
8
8
	a. Dấu hiệu cần tìm hiểu ở đây là gì?
	b. Hãy lập bảng tần số và tính điểm trung bình bài kiểm tra? 	
 c. Tìm mốt của dấu hiệu 
Câu 2: (2.5 điểm) 
 Cho các đa thức:	H(x) = x3 - 2x2 + 5x – 10
	G(x) = – 2x3 + 3x2 - 8x - 1
 a. Tìm bậc của đa thức H(x)
Tính giá trị của đa thức H(x) tại x = 2; x = -1
Tính G(x) + H(x); G(x) – H(x)
Câu 3: (5 điểm)
Cho D ABC cân tại A (); các đường cao BD; CE (D Î AC; E Î AB) cắt nhau tại H
Chứng minh D ABD = D ACE
Chứng minh D BHC là tam giác cân
So sánh HB và HD
Trên tia đối của tia EH lấy điểm N sao cho NH < HC; Trên tia đối của tia DH lấy điểm M sao cho MH = NH . Chứng minh các đường thẳng BN; AH; CM đồng quy
Câu 4: (0,5 điểm)
Chứng minh rằng đa thức P(x) có ít nhất hai nghiệm biết rằng: 
	x.P(x +2) – (x -3).P(x -1) = 0
TRƯỜNG THCS CỬA NAM
HƯỚNG DẪN CHẤM MÔN TOÁN 7 - HỌC KỲ II
Câu
ĐÁP ÁN
ĐIỂM
1 
(2 điểm)
a. Điểm kiểm tra một tiết môn Toán của mỗi học sinh lớp 7A
b Bảng tần số:
Giá trị (x)
1
2
4
5
7
8
9
10
Tần số (n)
1
3
4
7
5
3
4
3
N = 30
. Số trung bình cộng:
c. Mo = 5
0.5
0.5
0.5
0.5
2
(2,5 điểm)
a. Bậc của đa thức H(x): 3
b. H(2) = 23 – 2.22 + 5. 2 – 10= 	 8 – 8 + 10 – 10 = 0
 H(-1) = (-1)3 – 2.(-1)2 + 5. (-1) – 10 = -1 – 2.1 - 5 + 10 = 2 c.G(x) + H(x) = (– 2x3 + 3x2 - 8x – 1) + (x3 - 2x2 + 5x – 10) 
 = -2x3 + 3x2 – 8x – 1 + x3 – 2x2 + 5x - 10
 = (-2x3 + x3) + (3x2 – 2x2) + ( – 8x + 5x ) – (10+1)
 = -x3 + x2 - 3x - 11
G(x) - H(x) = (– 2x3 + 3x2 - 8x – 1) - (x3 - 2x2 + 5x – 10) 
 = – 2x3 + 3x2 - 8x – 1 - x3 + 2x2 - 5x + 10
 = (-2x3 - x3) + (3x2 + 2x2) - (8x + 5x) + (-1+ 10)
 = -3x3 + 5x2 - 13x + 9
0.5
0.5
0.5
0.25
0.25
0.25
0.25
3
(5 điểm)
0.5
a. Xét D ABD và D BCE có: (gt)
 BA = AC (gt)
 chung
Þ D ABD = D ACE (cạnh huyền – góc nhọn) 
1.5
b. D ABD = D ACE Þ (hai góc tương ứng)
 mặt khác: (D ABC cân tại A ) 
Þ Þ 
 Þ D BHC là tam giác cân
0.25
0.25
0.25
0.25
c. D HDC vuông tại D nên HD <HC
mà HB = HC ( D AIB cân tại H) 
Þ HD < HB
0.5
0.5
0.5
d. Gọi I là giao điểm của BN và CM
Xét D BNH và D CMH có:
BH = CH ( D BHC cân tại H)
 (đối đỉnh)
NH = HM (gt)
Þ D BNH = D CMH (c.g.c) Þ 
Lại có: (Chứng minh câu b)
Þ Þ 
Þ IBC cân tại I Þ IB = IC (1)
Mặt khác ta có: AB = AC (D ABC cân tại A) (2)
 HB = HC (D HBC cân tại H) (3)
Từ (1); (2) và (3) Þ 3 điểm I; A; H cùng nằm trên đường trung trực của BC 
Þ I; A; H thẳng hàng Þ các đường thẳng BN; AH; CM đồng quy
025
0.25
4
(0,5 điểm)
Với x = 0 Ta có:
0.P(0 + 2) – (0 – 3).P(0 – 1) = 0 Û 0 + 3P(-1) = 0 Û P(-1) =0
Þ x = -1 là nghiệm của đa thức P(x)
Với x = 3 ta có:
3.P(3 + 2) – (3 – 3) .P(3 – 1) = 0 Û 3.P(5) - 0.P(2) = 0
Û 3.P(5) = 0 Û P(5) = 0 
Þ x = 5 là nghiệm của đa thức P(x)
Vậy đa thức P(x) có ít nhất 2 nghiệm là -1 và 0
0.25
0.25
Lưu ý: Học sinh làm cách khác đúng, vẫn cho điểm tối đa