Đề kiểm tra định kì năm học 2015 - 2016 môn: Toán 9 phần đại số lớp 9 tiết: 59 thời gian làm bài 45 phút

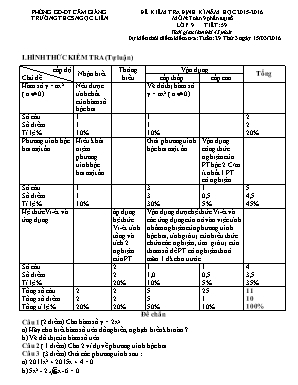
PHÒNG GD-ĐT CẨM GIÀNG
TRƯỜNG THCS NGỌC LIÊN
ĐỀ KIỂM TRA ĐỊNH KÌ NĂM HỌC 2015-2016
 MÔN: Toán 9 phần đại số 
LỚP 9 TIẾT: 59
Thời gian làm bài 45 phút
 Dự kiến thời điểm kiểm tra: Tuần: 29 Thứ 3 ngày 15/03/2016 
I.HÌNH THỨC KIỂM TRA (Tự luận)
cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
cấp thấp
cấp cao
Hàm số y = ax2
( a 0) 
Nêu được tính chất của hàm số bậc hai
Vẽ đồ thị hàm số 
y = ax2 ( a 0)
Số câu
Số điểm 
Tỉ lệ %
1
1
10%
1
1
10%
2
2
20%
Phương trình bậc hai một ẩn
Hiểu khái niệm phương trình bậc hai một ẩn
Giải phương trình bậc hai một ẩn
Vận dụng công thức nghiệm của PT bậc 2 C/m ít nhất 1 PT có nghiệm 
Số câu
Số điểm 
Tỉ lệ %
1
1
10%
3
3
30%
1
0,5
5%
5
4,5
45%
Hệ thức Vi-ét và ứng dụng
áp dụng hệ thức Vi-ét tính tổng và tích 2 nghiệm của PT
Vận dụng được hệ thức Vi-ét và các ứng dụng của nó vào việc tính nhẩm nghiệm của phương trình bậc hai, tính giá trị của biểu thức chứa các nghiệm , tìm giá trị của tham số để PT có nghiệm thoả mãn 1 đk cho trước.
Số câu
Số điểm 
Tỉ lệ %
2
2
20%
1
1,0
10%
1
0,5
5%
4
3,5
35%
Tổng số câu
Tổng số điểm 
Tổng tỉ lệ %
2
2
20%
2
2
20%
5
5
50%
25
1
10%
11
10
100%
Đề chẵn
Câu 1.(2 điểm) Cho hàm số y = 2x2
a) Hãy cho biết hàm số trên đồng biến, nghịch biến khi nào ?
b) Vẽ đồ thị của hàm số trên
Câu 2.( 1 điểm) Cho 2 ví dụ về phương trình bậc hai. 
Câu 3. (3 điểm) Giải các phương trình sau :
a) 2011x2 + 2015x + 4 = 0
b) 5x2 - 2x- 6 = 0
c) 8x2 - 450 = 0
Câu 4. ( 4 điểm) Cho phương trình (ẩn x) : x2 - 6x + m = 0 (1)
a) Cho m = 1, không giải phương trình hãy tính x1+x2 ; x1x2 ; ( với x1, x2 là hai nghiệm của phương trình )
b) Tìm giá trị của m để phương trình (1)có hai nghiệm phân biệt x1, x2 thoả mãn x12 + x22 = 26
c) Chứng tỏ rằng trong hai phương trình: phương trình (1) và phương trình 
x2-(2m+2)x+1=0 (2) (ẩn x) luôn tồn tại ít nhất một PT có hai nghiệm phân biệt với mọi m. 
Đáp án
Câu
ý
Đáp án
điểm
1
a
Nêu đúng tính đồng biến nghịch biến
0,5
b
chỉ rõ cách xác định các điểm thuộc đồ thị 
0,75
Vẽ đúng đồ thị
0,75
2
Cho hai ví dụ về pt bậc hai (mỗi ví dụ 0,5 đ)
1,0
3
a
Tính đúng 
0,5
giải đúng nghiệm x1 = -1 ; x2 = 
0,5
b
Tính đúng 
0,5
giải đúng nghiệm x1 = ; x2 = 
0,5
c
Tìm ra x2
0,5
giải đúng nghiệm x1 =; x2 = 
0,5
4
a
Thay m=1 đúng
0,5
Chứng minh >0
0,5
tìm đúng x1+ x2=6
0,5
x1x2 = 1
0,5
Chỉ ra x1, x2 dương, tính được 
0,5
biến đổi 
thay số tính đúng kết quả =2+
( nếu không chỉ ra x1, x2 dương mà vẫn tính đúng thì trừ 0,5 đ)
0,25
0,25
b
= 9 - m
Pt có 2 nghiệm phân biệt 
0,25
Theo hệ thức Vi-ét x1+ x2=6 ; x1x2 = m
Theo bài ra x12 + x22 =26 (x1+x2)2 - 2x1x2 = 26
 36-2m = 26 m=5 ( TM)
Vậy m = 5
0,25
c
Tính 2’=m2+2m
Xét +2’= m2+2m+9-m=m2+m+9
=>0 với mọi m
0,25
Do đó luôn tồn tại ít nhất hoặc 2’ có giá trị dương.
Suy ra tồn tại ít nhất một trong hai PT đã cho có hai nghiệm phân biệt với mọi giá trị m.
0,25
Đề lẻ
Câu 1.(2 điểm) Cho hàm số y = -2x2
a) Hãy cho biết hàm số trên đồng biến, nghịch biến khi nào ?
b) Vẽ đồ thị của hàm số trên
Câu 2.( 1 điểm) Cho 2 ví dụ về phương trình bậc hai. 
Câu 3. (3 điểm) Giải các phương trình sau :
a) 2014x2 + 2016x + 2 = 0
b) 11x2 - 2x- 2 = 0
c) 20x2 - 450 = 0
Câu 4. ( 4 điểm) Cho phương trình (ẩn x) : x2 - 6x + k = 0 (1)
a) Cho k = 2, không giải phương trình hãy tính x1+x2; x1x2; ( với x1, x2 là hai nghiệm của phương trình).
b) Tìm giá trị của k để phương trình (1) có hai nghiệm phân biệt x1, x2 thoả mãn x12+x22 =26.
c) Chứng tỏ rằng trong hai phương trình: phương trình (1) và phương trình 
x2-(2k+2)x+1=0 (2) (ẩn x) luôn tồn tại ít nhất một PT có hai nghiệm phân biệt với mọi k.
Đáp án
Câu
ý
Đáp án
điểm
1
a
Nêu đúng tính đồng biến nghịch biến
0,5
b
chỉ rõ cách xác định các điểm thuộc đồ thị 
0,75
Vẽ đúng đồ thị
0,75
2
Cho hai ví dụ về pt bậc hai (mỗi ví dụ 0,5 đ)
1,0
3
a
Tính đúng 
0,5
giải đúng nghiệm x1 = -1 ; x2 = 
0,5
b
Tính đúng 
0,5
giải đúng nghiệm x1 = ; x2 = 
0,5
c
Tìm ra x2
0,5
giải đúng nghiệm x1 =; x2 = 
0,5
4
a
Thay k =2 đúng
0,5
Chứng minh >0
0,5
tìm đúng x1+ x2=6
0,5
x1x2 = 2
0,5
Chỉ ra x1, x2 dương, tính được 
0,5
biến đổi 
thay số tính đúng kết quả =2+
( nếu không chỉ ra x1, x2 dương mà vẫn tính đúng thì trừ 0,5 đ)
0,25
0,25
b
= 9 - k
Pt có 2 nghiệm phân biệt 
0,25
Theo hệ thức Vi-ét x1+ x2=6 ; x1x2 = k
Theo bài ra x12 + x22 =26 (x1+x2)2 - 2x1x2 = 26
 36-2k = 26 k=5 ( TM)
Vậy k = 5
0,25
c
Tính 2’=k2+2k
Xét +2’= k2+2k+9-k=k2+k+9
=với mọi k
0,25
Do đó luôn tồn tại ít nhất hoặc 2’ có giá trị dương.
Suy ra tồn tại ít nhất một trong hai PT đã cho có hai nghiệm phân biệt với mọi giá trị k.
0,25
II. HDVN: Ôn tập lại HT Vi-et, đọc trước bài phương trình quy về PT bậc hai.
GIÁO VIÊN DUYỆT ĐỀ
( Ký và ghi rõ họ tên) 
Vũ Thị Huỳnh Nga
 GIÁO VIÊN RA ĐỀ 
 ( Ký và ghi rõ họ tên) 
 Phạm Thị Mỹ Dung
BGH KÝ DUYỆT ĐỀ
Đề chẵn
Câu 1.(2 điểm) Cho hàm số y = 2x2
a) Hãy cho biết hàm số trên đồng biến, nghịch biến khi nào ?
b) Vẽ đồ thị của hàm số trên
Câu 2.( 1 điểm) Cho 2 ví dụ về phương trình bậc hai. 
Câu 3. (3 điểm) Giải các phương trình sau :
a) 2011x2 + 2015x + 4 = 0
b) 5x2 - 2x- 6 = 0
c) 8x2 - 450 = 0
Câu 4. ( 4 điểm) Cho phương trình (ẩn x) : x2 - 6x + m = 0 (1)
a) Cho m = 1, không giải phương trình hãy tính x1+x2 ; x1x2 ; ( với x1, x2 là hai nghiệm của phương trình )
b) Tìm giá trị của m để phương trình (1)có hai nghiệm phân biệt x1, x2 thoả mãn:
x12 + x22 = 26
c) Chứng tỏ rằng trong hai phương trình: phương trình (1) và phương trình 
x2-(2m+2)x+1=0 (2) (ẩn x) luôn tồn tại ít nhất một PT có hai nghiệm phân biệt với mọi m. 
Đề lẻ
Câu 1.(2 điểm) Cho hàm số y = -2x2
a) Hãy cho biết hàm số trên đồng biến, nghịch biến khi nào ?
b) Vẽ đồ thị của hàm số trên
Câu 2.( 1 điểm) Cho 2 ví dụ về phương trình bậc hai. 
Câu 3. (3 điểm) Giải các phương trình sau :
a) 2014x2 + 2016x + 2 = 0
b) 11x2 - 2x- 2 = 0
c) 20x2 - 450 = 0
Câu 4. ( 4 điểm) Cho phương trình (ẩn x) : x2 - 6x + k = 0 (1)
a) Cho k = 2, không giải phương trình hãy tính x1+x2; x1x2; ( với x1, x2 là hai nghiệm của phương trình).
b) Tìm giá trị của k để phương trình (1) có hai nghiệm phân biệt x1, x2 thoả mãn:
 x12+x22 =26.
c) Chứng tỏ rằng trong hai phương trình: phương trình (1) và phương trình 
x2-(2k+2)x+1=0 (2) (ẩn x) luôn tồn tại ít nhất một PT có hai nghiệm phân biệt với mọi k.