Đề kiểm tra , đánh giá giữa kì 2 môn Toán Lớp 9 - Năm học 2021-2022

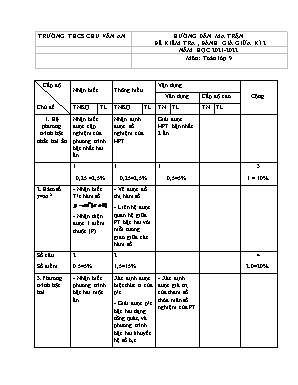
TRƯỜNG THCS CHU VĂN AN
HƯỚNG DẪN MA TRẬN
 ĐỀ KIỂM TRA , ĐÁNH GIÁ GIỮA KÌ 2
NĂM HỌC 2021-2022
Môn: Toán lớp 9
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Vân dụng
Cấp độ cao
TNKQ
TL
TNKQ
TL
TN
TL
TN
TL
1. Hệ phương trình bậc nhất hai ẩn
Nhận biết được cặp nghiệm của phương trình bậc nhất hai ẩn
Nhận định được số nghiệm của HPT
Giải được HPT bận nhất 2 ẩn
1
0,25 =2,5%
1
0,25=2,5%
1
0,5=5%
3
1 = 10%
2.Hàm số y=ax2
- Nhận biết T/c hàm số 
- Nhận diện được 1 điểm thuộc (P)
- Vẽ được đồ thị hàm số
- Liên hệ được quan hệ giữa PT bậc hai với mỗi tương giao giữa các hàm số
Số câu
Số điểm
2
0.5=5%
2
1,5=15%
4
2.0=20%
3.Phương trình bậc hai 
- Nhận biết phương trình bậc hai một ẩn
Xác định được biệt thức ∆ của p/t
- Giải được p/t bậc hai dạng tổng quát, và phương trình bậc hai khuyết hệ số b,c.
- Xác định được giá trị của tham số thỏa mãn số nghiệm của PT
Số câu
Số điểm
1 0.25=2,5%
3
1.25=12,5%
1
0.5=5%
5
2,0=20%
4.Hệ thức 
Vi-et và áp dụng
Tìm tham số để PT thỏa mãn đ/k về nghiệm.
Biến đổi tính toán giá trị 1 biểu thức theo tham số
Số câu
Số điểm
1
0,5=5%
1
0,5=5%
2
1,0=10%
5. Góc với đường tròn
Nhận biết góc, tính chất của góc, tính góc
Nhận biết tứ giác nội tiếp đường tròn 
- Vận dụng tính chất của các góc trong một đường tròn để chứng minh ba điểm thẳng hàng.
- Vận dụng tính chất của các góc trong một đường tròn để chứng minh đẳng thức tích; 
Số câu
Số điểm
5
2,0=20%
1
1,0=10%
1
1,0=10%
7
4=40%
Tổng số câu
Tổngsố điểm
9
3,0=30%
8
4,0=40%
3
2,0=20%
1
1,0=10%
21
10,0=100%
Hết
TRƯỜNG THCS CHU VĂN AN
ĐỀ KIỂM TRA , ĐÁNH GIÁ GIỮA KÌ 2
NĂM HỌC 2021-2022
Mã đề: 01
Môn: Toán lớp 9
Thời gian: 90 phút ( Không kể thời gian giao đề)
( Đề có: 02 trang)
	ĐỀ BÀI
PHẦN I. TRẮC NGHIỆM (2, 5 điểm) 
Em hãy viết chữ cái đứng trước mỗi câu trả lời đúng vào bài kiểm tra:
Câu 1. Hệ phương trình : có bao nhiêu nghiệm?
 	A. Vô nghiệm. 	B. Vô số nghiệm. 	
C. Hai nghiệm. 	D. Một nghiệm duy nhất.
Câu 2. Cặp số là nghiệm của hệ phương trình nào sau đây?
A. .	B. .	C. .	D. .
Câu 3. Cho hàm số với .Kết luận nào sau đây là đúng?
A. Hàm số đồng biến khi và .	B. Hàm số đồng biến khi và .	
C. Hàm số đồng biến khi và .	D. Hàm số đồng biến khi và .
Câu 4. Cho hàm số có đồ thị là Parabol (P). Trong các điểm có tọa độ dưới đây điểm nào thuộc (P)
A. ( 1; 2).	B. ( 2; 3).	C. ( -3; 9).	D. (-1; -2).
Câu 5. Phương trình nào dưới đây là phương trình bậc hai một ẩn?
A. 	 B...	C. .	D. .
 Câu 6. Phương trình x2 – 3x + 7 = 0 có biệt thức ∆ bằng
A. 2.
B. -19.
C. -37.
D. 16.
Câu 7. Khẳng định nào sau đây là sai?
A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Trong một đường tròn, hai góc nội tiếp bằng nhau chắn hai cung bằng nhau.
C. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
D. Trong một đường tròn, hai góc nội tiếp cùng chắn cung một cung thì bằng nhau.
Câu 8: Góc có đỉnh bên ngoài đường tròn có số đo:
A. Bằng số đo cung lớn bị chắn	B. Bằng nửa tổng số đo hai cung bị chắn.
C. Bằng nửa hiệu số đo hai cung bị chắn.	D. Bằng số đo cung nhỏ bị chắn.
Câu 9. Cho tứ giác nội tiếp. Chọn câu sai.
A. .	B. .	C. .	D. .
Câu 10. Cho hình vẽ bên, biết số đo góc Số đo góc ở hình vẽ bên là:
A..	 B..	 
C.. 	D..
PHẦN II. TỰ LUẬN (7, 5 điểm)
Bài 1(1,5 điểm). Giải các hệ phương trình và phương trình sau:
a, 	b, 	c, 
Bài 2. (1,5 điểm) Cho hàm số y = x2 có đồ thị là (P)
a, Vẽ (P)
b, Tìm k để đường thẳng (d) y = 2x – k +1 tiếp xúc với (P).
Bài 3. (1 điểm) Cho phương trình x2 + 2x + m = 0 (*)
a, Với giá trị nào của m thì phương trình có hai nghiệm phân biệt.
b, Tìm m để phương trình có hai nghiệm x1 và x2 thoả x12 + x22 = 5.
c, Gọi là 2 nghiệm của của phương trình (*). Tính giá trị của biểu thức theo m
Bài 4. (3,0 điểm). Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh:
 	a, Các tứ giác: BCKM nội tiếp đường tròn. 
 b, CK.CD = CA.CB 
 c, Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
------------------ Hết -----------------
TRƯỜNG THCS CHU VĂN AN
HƯỚNG DẪN CHẤM ĐIỂM, ĐÁNH GIÁ GIỮA KÌ 2
NĂM HỌC 2021-2022
Mã: 01
Môn: Toán lớp 9
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM 
I. TRẮC NGHIỆM
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
D
C
B
A
A
B
C
C
D
A
Điểm
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
II. TỰ LUẬN
Bài
Nội dung
Điểm
1
a, 
b, 
Vậy S = 
c, 
Biết áp dụng công thức nghiệm, hoặc nhầm nghiệm
Giải được PT tìm được tập nghiệm: 
0,25
0,25
0,25
0,25
0,25
0,25
2
Bảng giá trị của hàm số : y = x2 
x
-2
-1
0
1
2
y = x2
4
1
0
1
4
b) HS lập PT hoành độ giao điểm và tính D đúng
Lập luận dẫn đến kết quả k = 2
0,5
0,5
0,5
3
x2 + 2 x + m = 0
a) Học sinh tính đúng D ( hoặc D’ ) 
 Lập luận dẫn đến m<1
b) Đúng hệ thức Vi-et 
 Lập luận dẫn đến 
c, Tính giá trị của biểu thức theo m
0,25
0,25
0,25
0,25
0,25
0,25
0, 25
a) (gt)
 ( góc nội tiếp chắn nửa đường tròn)
Suy ra Tứ giác BCKM nội tiếp 
0,25
0,25
0,25
b) Xét hai tam giác ACK và DCB có: 
 ( cùng bù với góc CKM)
Do đó đồng dạng với 
 Suy ra CK.CD = CA.CB
0,25
0,25
0,25
0,25
c) Chứng minh BK ^ AD ( Vì BK là đường cao thứ 3 của tam giác ABD Chứng minh góc BNA = 900 ( góc nt chắn nửa đường tròn) => BN ^ AD
Vì qua điểm B chỉ có duy nhất một đường thẳng vuông góc với AD 
Kết luận B, K, N thẳng hàng
0,25
0,25
0,25
0,25
TRƯỜNG THCS CHU VĂN AN
ĐỀ KIỂM TRA , ĐÁNH GIÁ GIỮA KÌ 2
NĂM HỌC 2021-2022
Mã đề: 02
Môn: Toán lớp 9
Thời gian: 90 phút ( Không kể thời gian giao đề)
( Đề có: 02 trang)
	ĐỀ BÀI
PHẦN I. TRẮC NGHIỆM (2, 5 điểm) 
Em hãy viết chữ cái đứng trước mỗi câu trả lời đúng vào bài kiểm tra:
Câu 1. Cặp số là nghiệm của hệ phương trình nào sau đây?
	A. .	B. .	C. .	D. .
Câu 2. Phương trình x2 – 3x + 7 = 0 có biệt thức ∆ bằng
	A. 16.	B. -37.	C. -19.	D. 2.
Câu 3. Hệ phương trình : có bao nhiêu nghiệm?
	A. Một nghiệm duy nhất.	B. Hai nghiệm.
	C. Vô số nghiệm.	D. Vô nghiệm.
Câu 4. Cho hàm số có đồ thị là Parabol (P). Trong các điểm có tọa độ dưới đây điểm nào thuộc (P)
	A. ( 2; 3).	B. (-1; -2).	C. ( -3; 9).	D. ( 1; 2).
Câu 5. Góc có đỉnh bên ngoài đường tròn có số đo:
	A. Bằng số đo cung lớn bị chắn	B. Bằng nửa tổng số đo hai cung bị chắn.
	C. Bằng nửa hiệu số đo hai cung bị chắn.	D. Bằng số đo cung nhỏ bị chắn.
Câu 6. Cho hàm số với .Kết luận nào sau đây là đúng?
	A. Hàm số đồng biến khi và .	B. Hàm số đồng biến khi và .
	C. Hàm số đồng biến khi và .	D. Hàm số đồng biến khi và .
Câu 7. Khẳng định nào sau đây là sai?
	A. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
	B. Trong một đường tròn, hai góc nội tiếp cùng chắn cung một cung thì bằng nhau.
	C. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.
	D. Trong một đường tròn, hai góc nội tiếp bằng nhau chắn hai cung bằng nhau.
Câu 8. Cho hình vẽ bên, biết số đo góc Số đo góc ở hình vẽ bên là: 
	A. .	B. .	
	C. .	D. .
Câu 9. Phương trình nào dưới đây là phương trình bậc hai một ẩn?
	A. . B. .	C. ..	D. 
Câu 10. Cho tứ giác nội tiếp. Chọn câu sai.
A. . B. . C. . D. .
PHẦN II. TỰ LUẬN (7, 5 điểm)
Bài 1(1,5 điểm). Giải các hệ phương trình và phương trình sau:
a, 	b, 	c, 
Bài 2. (1,5 điểm) Cho hàm số y = x2 có đồ thị là (P)
a, Vẽ (P)
b, Tìm k để đường thẳng (d) y = 2x – k +1 tiếp xúc với (P).
Bài 3. (1 điểm) Cho phương trình x2 + 2x + m = 0 (*)
a, Với giá trị nào của m thì phương trình có hai nghiệm phân biệt.
b, Tìm m để phương trình có hai nghiệm x1 và x2 thoả x12 + x22 = 5.
c, Gọi là 2 nghiệm của của phương trình (*). Tính giá trị của biểu thức theo m
Bài 4. (3,0 điểm). Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh:
 	a, Các tứ giác: BCKM nội tiếp đường tròn. 
 b, CK.CD = CA.CB 
 c, Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
------------------ Hết -----------------
TRƯỜNG THCS CHU VĂN AN
HƯỚNG DẪN CHẤM ĐIỂM, ĐÁNH GIÁ GIỮA KÌ 2
NĂM HỌC 2021-2022
Mã: 02
Môn: Toán lớp 9
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM 
I. TRẮC NGHIỆM
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
C
C
A
D
C
C
A
A
D
C
Điểm
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
II. TỰ LUẬN
Bài
Nội dung
Điểm
1
a, 
b, Vậy S = 
c, 
Biết áp dụng công thức nghiệm, hoặc nhầm nghiệm
Giải được PT tìm được tập nghiệm: 
0,25
0,25
0,25
0,25
0,25
0,25
2
Bảng giá trị của hàm số : y = x2 
x
-2
-1
0
1
2
y = x2
4
1
0
1
4
b) HS lập PT hoành độ giao điểm và tính D đúng
Lập luận dẫn đến kết quả k = 2
0,5
0,5
0,5
3
x2 + 2 x + m = 0
a) Học sinh tính đúng D ( hoặc D’ ) 
 Lập luận dẫn đến m<1
b) Đúng hệ thức Vi-et 
 Lập luận dẫn đến 
c, 
0,25
0,25
0,25
0,25
0,5
0, 25
a) (gt)
 ( góc nội tiếp chắn nửa đường tròn)
Suy ra Tứ giác BCKM nội tiếp 
0,25
0,25
0,25
b) Xét hai tam giác ACK và DCB có: 
 ( cùng bù với góc CKM)
Do đó đồng dạng với 
 Suy ra CK.CD = CA.CB
0,25
0,25
0,25
0,25
c) Chứng minh BK ^ AD ( Vì BK là đường cao thứ 3 của tam giác ABD Chứng minh góc BNA = 900 ( góc nt chắn nửa đường tròn) => BN ^ AD
Vì qua điểm B chỉ có duy nhất một đường thẳng vuông góc với AD 
Kết luận B, K, N thẳng hàng
0,25
0,25
0,25
0,25