Đề kiểm tra chương V môn: Toán - Khối 11 thời gian: 45 phút

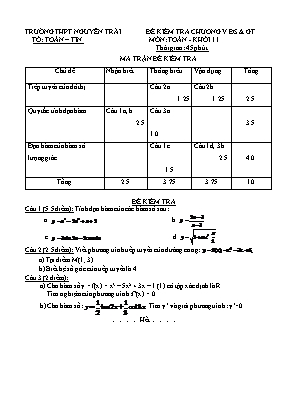
TRƯỜNG THPT NGUYỄN TRÃI. ĐỀ KIỂM TRA CHƯƠNG V ĐS & GT
	TỔ: TOÁN – TIN.	 MÔN: TOÁN - KHỐI 11
 Thời gian: 45 phút.
MA TRẬN ĐỀ KIỂM TRA
Chủ đề
Nhận biết 
Thông hiểu
Vận dụng
Tổng
Tiếp tuyến của đồ thị
Câu 2a
 1.25
Câu 2b
 1.25
2.5
Quy tắc tính đạo hàm
Câu 1a, b
 2.5
Câu 3a
 1.0
3.5
Đạo hàm của hàm số lượng giác
Câu 1c
 1.5
Câu 1d, 3b
 2.5
4.0
Tổng
2.5
3.75
3.75
10
ĐỀ KIỂM TRA
Câu 1 (5.5 điểm): Tính đạo hàm của các hàm số sau:
	 a. 	 b. 	
 c. d. 
Câu 2 (2.5 điểm): Viết phương trình tiếp tuyến của đường cong: 
	a) Tại điểm M(1; 3) 
	b) Biết hệ số góc của tiếp tuyến là 4.
Câu 3 (2 điểm): 
 a) Cho hàm số y = f(x) = x3 – 5x2 + 3x – 1 (1) có tập xác định là R.
 Tìm nghiệm của phương trình: f’(x) = 0
 b) Cho hàm số: . Tìm y’ và giải phương trình: y’=0.
 .Hết..
ĐÁP ÁN 
Câu
Đáp án
Điểm
1
a. (1 điểm). Ta có :
y’ = 
y’ = 3x2 – 4x + 1
b. (1,5 điểm). Ta có:
y' = 
y’ = 
y’ = 
c. (1,5 điểm). Ta có:
 y’ = (3sin2x – 5cos4x)’ 
 y’ = (3sin2x)’ – (5cos4x)’
d. (1,5 điểm). Ta có:
 0.5
 0.5
 0.5
0.5
0.5
0.5
0.5
0.5
0.75
0.75
2
a. (1,25 điểm). Hàm số: 
Ta có: x0 = 1 và y0 = 3
Nên: f’(x0) = f’(1) = -1
Vậy phương trình tiếp tuyến: y = -(x -1) + 3
	 y = -x + 4
b. (1,25 điểm). Vì hệ số góc của tiếp tuyến là 4 nên 
f’(x0 ) = 4
nên x0 = và y0 = 
Vậy phương trình tiếp tuyến: y = 4(x -) + 
	 y = 4x - 
0.25
0.25
0.5
0.25
0.25
0.5
0.25
0.25
3
a. (1,0 điểm). Hàm số : y = f(x) = x3 – 5x2 + 3x – 1 (1) có tập xác định là R.
Ta có: y’ = f’(x) = 3x2 – 10x + 3
f’(x) = 0 Û 3x2 – 10x + 3 = 0
 Û 
Vậy phương trình : f ‘ (x) = 0 có 2 nghiệm : 
b. (1,0 điểm).
 (*) sin22x = cos23x
0.5
0.25
0.25
0,25
0,25
0,25
0,25
.Hết.
BGH Duyệt: Tổ Trưởng Duyệt:
Võ Anh Tài. Nguyễn Hữu Dũng.
 Giáo Viên Ra Đề: Đặng Ngọc Liên.