Đề kiểm tra chất lượng học kì II môn Toán 7 - Năm học 2020-2021 - Đề số 2

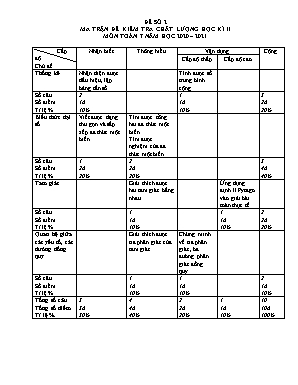
ĐỀ SỐ 2
MA TRẬN ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ II
MÔN TOÁN 7 NĂM HỌC 2020– 2021
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Thống kê
Nhận diện được dấu hiệu, lập bảng tần số
Tính được số trung bình cộng
Số câu
Số điểm
Tỉ lệ %
2
1đ
10%
1
1đ
10%
3
2đ
20%
Biểu thức đại số
Viết được dạng thu gọn và sắp xếp đa thức một biến
Tìm được tổng hai đa thức một biến.
Tìm được nghiệm của đa thức một biến
Số câu
Số điểm
Tỉ lệ %
1
2đ
20%
2
2đ
20%
3
4đ
40%
Tam giác
Giải thích được hai tam giác bằng nhau
Ứng dụng định lí Pytago vào giải bài toán thực tế.
Số câu
Số điểm
Tỉ lệ %
1
1đ
10%
1
1đ
10%
2
2đ
20%
Quan hệ giữa các yếu tố, các đường đồng quy
Giải thích được tia phân giác của tam giác
Chứng minh về tia phân giác, ba đường phân giác đồng quy
Số câu
Số điểm
Tỉ lệ %
1
1đ
10%
1
1đ
10%
2
1đ
10%
Tổng số câu
Tổng số điểm
Tỉ lệ %
3
3đ
30%
4
4đ
40%
2
2đ
20%
1
1đ
10%
10
10đ
100%
SỞ GIÁO DỤC VÀ ĐÀO TẠO	 KIỂM TRA HỌC KỲ II
TỈNH  	 Năm học: 2020-2021
	Môn thi: TOÁN - Lớp 7
	 Thời gian: 90 phút (không kể thời gian phát đề)
 Ngày thi :  /  / 2021
ĐỀ ĐỀ XUẤT
(Đề gồm có 01 trang)
Câu 1(2đ): Thời gian giải một bài toán (tính theo phút) của 30 học sinh được ghi lại trong bảng dưới đây:
8
5
7
8
9
7
8
9
12
8
6
7
7
7
9
8
7
6
12
8
8
7
7
9
9
7
9
6
5
12
 	a/ Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu? 
 	b/ Lập bảng “tần số” . 
 	c/ Tính số trung bình cộng (làm tròn một chữ số thập phân).
Câu 2(3đ): Cho hai đa thức f(x) = 5 +3x2 – x - 2x2 và g(x) = 3x + 3 – x – x2 
 	a/ Thu gọn và sắp xếp hai đa thức theo lũy thừa giảm dần của biến.
	b/ Tính h(x) = f(x) + g(x).
Câu 3(1đ): Tìm nghiệm của đa thức A(x) = x2 – 4x 
Câu 4(3đ): Cho tam giác ABC nhọn và cân tại A, đường cao AH (HBC).
	a/ Hai tam giác ABH và ACH có bằng nhau không? Vì sao?
	b/ Tia AH có phải là tia phân giác của góc BAC không? Vì sao?
	c/ Kẻ tia phân giác BK (KAC) của góc ABC. Gọi O là giao điểm của AH và BK. Chứng minh rằng CO là tia phân giác của góc ACB.
Câu 5(1đ): Một mảnh đất dạng hình chữ nhật ABCD có chiều dài và chiều rộng như hình 1. Hỏi một người muốn đi từ góc B đến góc D thì đi theo đường nào là ngắn nhất và độ dài đường đó là bao nhiêu mét?
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH .
HƯỚNG DẪN 
CHẤM CHÍNH THỨC
(gồm có 01 trang)
ĐÁP ÁN KIỂM TRA HỌC KÌ II
Năm học: 2020-2021
Môn thi: TOÁN 7 
Ngày thi: ..//2021
Câu
Nội dung
Điểm
Câu 1 (2đ)
a/ - Dấu hiệu là thời gian làm một bài toán của 30 học sinh.
 - Số các giá trị của dấu hiện là 30.
0,25
0,25
b/ Bảng tần số:
Giá trị (x)
5
6
7
8
9
12
Tần số (n)
2
3
9
7
6
3
N = 30 
0,5
c/ = == 7,9
0,5 - 0,25 - 0,25 
Câu 2 (3đ)
a/ f(x) = 5 +3x2 – x - 2x2 = x2 – x + 5
 g(x) = 3x + 3 – x – x2 = - x2 + 2x + 3
1,0
1,0
b/ h(x) = f(x) + g(x) = x2 – x + 5 - x2 + 2x + 3 = x + 8
0,5 – 0,5 
Câu 3 (1đ)
A(x) = x2 – 4x = 0
 x(x – 4)
 x = 0 hoặc x – 4 = 0
 x = 0 hoặc x = 4 
Vậy A(x) có 2 nghiệm: x = 0; x = 4.
0,25
0,25
0,25
0,25
Câu 4 (3đ)
a/ Hai tam giác ABH và ACH bằng nhau theo trường hợp cạnh huyền cạnh góc vuông.
 Bởi vì hai tam giác ABH và ACH là hai tam giác vuông
có 
0,5
0,5
b/ Tia AH là tia phân giác của góc BAC. 
 Bởi vì tam giác ABC cân tại A có AH là đường cao.
0,5
0,5
c/ Ta có AH và BK là hai đường phân giác của tam giác ABC cắt nhau tại O nên CO là đường phân giác thứ ba. Vậy CO là tia phân giác của góc ACB.
0,5 – 0,5
Câu 5 (1đ)
Một người muốn đi từ góc B đến góc D thì đi theo đường thẳng từ B đến D là ngắn nhất, độ dài đường đi là độ dài đoạn thẳng BD.
Áp dụng định lý Py ta go vào tam giác vuông ABD ta có:
 BD2 = AB2 + AD2 = 802 + 602 = 10 000
 BD = 100.
Vậy độ dài đường ngắn nhất đi từ B đến D là 100m.
0,5
0,25
0,25
* Chú ý: Học sinh có cách giải khác đúng vẫn cho điểm tối đa.