Đề kiểm tra 1 tiết hình học 8 – Chương III môn : Toán lớp : 8

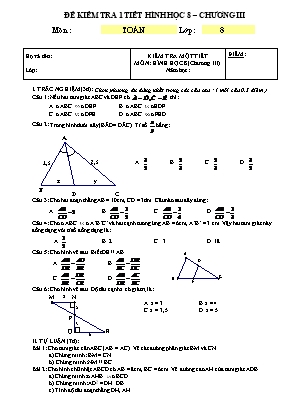
ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC 8 – CHƯƠNG III
Môn :
 TOÁN 
Lớp :
 8
Họ và tên: .
Lớp: .. 
KIỂM TRA MỘT TIẾT
MÔN: HÌNH HỌC 8 (Chương III)
Năm học: 
ĐIỂM:
I. TRẮC NGHIỆM (3đ): Chọn phương án đúng nhất trong các câu sau : ( mỗi câu 0,5 điểm )
Câu 1: Nếu hai tam giác ABC và DEF có thì:
A. DABC DDEF	B. DABC DEDF	
C. DABC DDFE 	D. DABC DFED
Câu 2: Trong hình dưới đây (BÂD= DÂC). Tỉ số bằng:
A. 	B. 	C. 	D. 
2,5
1,5
y
x
C
D
B
A
Câu 3: Cho hai đoạn thẳng AB = 10cm, CD = 3dm. Câu nào sau đây đúng:
A. 	B. 	C. 	D. 
Câu 4: Cho DABC DA’B’C’ và hai cạnh tương ứng AB = 6cm, A’B’ = 3 cm. Vậy hai tam giác này đồng dạng với tỉ số đồng dạng là:
B
C
A
E
D
	A. 	B. 2	C . 3	D. 18 
Câu 5: Cho hình vẽ sau. Biết DE // AB
A. 
B. 
C. 
D. 
6
3
2
x
P
M
N
Q
R
Câu 6: Cho hình vẽ sau. Độ dài cạnh x có giá trị là:
A. x = 3
B. x = 4
C. x = 3,5
D. x = 5
II. TỰ LUẬN (7đ): 
Bài 1: Cho tam giác cân ABC (AB = AC). Vẽ các đường phân giác BM và CN.
a) Chứng minh: BM = CN 
b) Chứng minh: NM // BC
Bài 2: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Vẽ đường cao AH của tam giác ADB.
a) Chứng minh: DAHB DBCD 
b) Chứng minh: AD2 = DH .DB 
c) Tính độ dài đoạn thẳng DH, AH.
	I. TRẮC NGHIỆM (3đ): 	
1
2
3
4
5
6
C
A
D
B
A
B
A
B
M
C
N
	II. TỰ LUẬN (7đ): (Theo ĐỀ 1)
	Bài 1: (2,5đ) 
- Hình vẽ đúng (0,5đ)
a) (1đ) Chứng minh: 
DABM = DACN ( hoặc DBNC = DCMB ) (0,75đ)
Þ BM = CN (0,25đ)
b) (1đ)
Vì DABM = DACN Þ AM = AN (0,25đ)
Có AB = AC (gt) (0,25đ)
Þ (0,25đ)
Þ NM // BC (theo Định lí đảo Talet) (0,25đ)
A
B
C
D
1
1
2
	Bài 2: (4,5đ) 
H
 - Hình vẽ đúng (0,5đ)
a) (1đ)
DAHB và DBCD có:
 (gt)
 (so le trong của AB // DC) (0,75đ)
Þ DAHB DBCD (g-g) (0,25đ)
b) (1,5đ) 
DABD và DHAD có:
 (gt) (0,25đ)
 : chung (0,25đ)
Þ DABD DHAD (g-g) (0,5đ)
Þ Þ AD2 = DH.DB (0,5đ)
c) (1,5đ) 
+ DABD ^ tại A có: AB = 8cm, AD = 6cm
Þ DB2 = AB2 + AD2 (Pytago) 
 = 82 + 62 =  = 102
Þ DB = 10 (cm) (0,25đ)
Theo chứng minh trên AD2 = DH.DB Þ (0,5đ)
+ Ta có: DABD DHAD (Cm trên) 
 (0,25đ)
 (0,5đ)
======================= Hết ======================