Đề khảo sát chất lượng học kì I năm học 2014 - 2015 môn: Toán 8 thời gian: 90 phút (đề tham khảo)

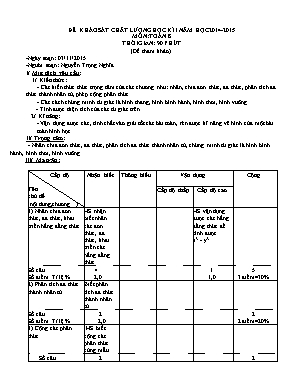
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KÌ I NĂM HỌC 2014-2015
MÔN: TOÁN 8
THỜI GIAN: 90 PHÚT
(Đề tham khảo)
Ngày soạn: 03/11/2015
Người soạn: Nguyễn Trọng Nghĩa
I/ Mục đích yêu cầu:
 1/ Kiến thức:
 - Các kiến thức thức trọng tâm của các chương như: nhân, chia đơn thức, đa thức, phân tích đa thức thành nhân tử, phép cộng phân thức.
 - Các cách chứng minh tứ giác là hình thang, hình bình hành, hình thoi, hình vuông.
 - Tính được diện tích của các tứ giác trên.
 2/ Kĩ năng:
- Vận dụng được các, tính chất vào giải tốt các bài toán, rèn được kĩ năng vẽ hình của một bài toán hình học
II/ Trọng tâm:
 - Nhân chia đơn thức, đa thức, phân tích đa thức thành nhân tử, chứng minh tứ giác là hình bình hành, hình thoi, hình vuông
 III/ Ma trận:
 Cấp độ
Tên 
chủ đề 
(nội dung,chương)
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1) Nhân chia đơn thức, đa thức, khai triển hằng đẳng thức
HS nhận biết nhân các đơn thức, đa thức, khai triển các hằng đẳng thức.
HS vận dụng được các hằng đẳng thức để tính được 
x3 - y3
Số câu 
Số điểm Tỉ lệ %
 4
 2,0
1
1,0
5
3 điểm=30%
2) Phân tích đa thức thành nhân tử
Biết phân tích đa thức thành nhân tử.
Số câu 
Số điểm Tỉ lệ %
2
2,0
2
2 điểm=20%
3) Cộng các phân thức
HS biết cộng các phân thức cùng mẫu.
 Số câu 
Số điểm Tỉ lệ %
2
1,0
2
1 điểm=10%
4) Tứ giác: hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông và diện tích các hình đó.
HS hiểu được cách tính góc của 1 tứ giác. Chứng minh được tứ giác là một hình thoi. Tính diện tích tam giác. GT + KL
HS vận dụng định lí tính được góc của tứ giác. Tìm điều kiện của tam giác để tứ giác là hình vuông.
Câu Số
Số điểm Tỉ lệ %
3
3,0
2
1,0
5
4 điểm=40%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
8
5.0
50%
3
3,0
30%
3
2,0
20%
14
10 điểm
IV/ Đề kiểm tra HKI: 
 A. Câu hỏi:
 I/. Lý thuyết (2điểm)
 	 Câu 1: (1,0 điểm) 
 a) Viết hằng đẳng thức bình phương của một tổng.
 	 b) Áp dụng: Khai triển hằng đẳng thức (x + 3)2 
 	 Câu 2: (1,0 điểm)
	 a) Phát biểu định lí về tổng các góc của một một tứ giác.
	 b) Cho tứ giác ABCD vuông ở A, biết = 300, = 800. Tính số đo góc D.
 II/. Bài tập (8điểm)
	 Bài 1: (2,0 điểm) 
 Phân tích các đa thức sau thành nhân tử:
 	a) x3 – 9x 	
	 b) x2 – 3x + xy – 3y	
	 Bài 2: (2,0 điểm) 
 Thực hiện các phép tính sau:
 	a) (x + 1)(x – 2)	
 	b) (4x4y4 – 12x2y2 ) : 4x2y2 
	 c) 
	 d) 
	 Bài 3: (1,0 điểm) 
 Cho x – y = 4 và x2 + y2 = 106. Tính x3 – y3.
Bài 4: (3,0điểm) 
Cho tam giác ABC vuông tại A, đường trung tuyến AM . Gọi P là trung điểm của AB, Q là điểm đối xứng với M qua P.
 a/ Chứng minh : Tứ giác AQBM là hình thoi.
 b/ Tính diện tích tam giác ABC, biết AB = 10cm, AC = 6cm.
 c/ Tam giác ABC cần điều kiện gì thì tứ giác AQBM là hình vuông ? 
 B. Đáp án
Câu/Bài
Nội dung
Điểm
I.Lý thuyết
1
(1,0 điểm)
a) (A + B)2 = A2 + 2AB + B2
b) (x + 3)2 = x2 + 6x + 9
0,5đ
0,5đ
2
(1,0 điểm)
a) Phát biểu đúng định lí: Tổng 4 góc của một tứ giác bằng 3600.
b) =3600 – (900+300+800) = 1600
0,5đ
0,5đ
II.Bài tập
1
(2,0điểm)
a) x3 – 9x 
 = x(x2 – 9) 
 = x(x – 3)(x + 3)	
b) x2 – 3x + xy – 3y = (x2 – 3x) + (xy – 3y)
	= x(x–3) +y(x–3)
	= (x–3)(x+y)
0,5đ
0,5đ
0,5đ
0,25đ
0,25đ
2
(2,0 điểm)
a) (x + 1)(x – 2) =x2 -2x +x -2 = x2 – x – 2	
b) (4x4y4 – 12x2y2 ) : 4x2y2 = x2y2 – 3	
c) 
 = 2x
d) 
 = 
 = x-1
0,5đ
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
3
(1,0 điểm)
x3 – y3 = (x – y)(x2 + y2 +xy)
 = (x – y)[x2 + y2 + ]
 = 4.(106 +) = 604
0.25đ
0.5đ
0.25đ
4
(3,0 điểm)
 HS vẽ hình ghi GT, KL 
a/ Chứng minh Tứ giác AQBM là hình thoi:
 Ta có: AP = BP ( gt ) và PM = PQ ( gt ) 
nên tứ giác AQBM là hình bình hành (t/c tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) 
 Mặt khác vì AM = MB ( t/c đường trung tuyến ứng với cạnh huyền của tam giác vuông )
 Vậy tứ giác AQBM là hình thoi.
b/ Tính diện tích tam giác ABC biết AB = 10cm, AC = 6cm.
 Tam giác ABC vuông tại A nên:
 SABC = AB . AC 
 = . 10 . 6 
 = 30 (cm2)
 c/ Tứ giác AQBM là hình vuông nghĩa là = 900 hay = 450
 tức là tam giác ABC là tam giác vuông cân tại A. 
0.5đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
 TTCM	GVBM
Nguyễn Thị Thanh Nguyễn Trọng Nghĩa