Đề đề xuất kiểm tra chất lượng học kì II môn: Toán – lớp 9 (Đề 9)

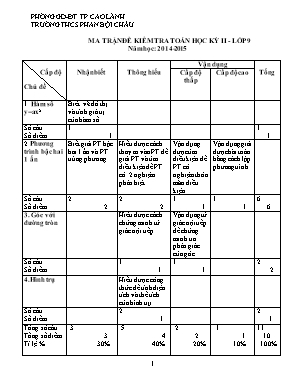
PHÒNG GD-ĐT TP CAO LÃNH
TRƯỜNG THCS PHAN BỘI CHÂU
 MA TRẬN ĐỀ KIỂM TRA TOÁN HỌC KỲ II - LỚP 9
 Năm học: 2014-2015
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp độ thấp
Cấp độ cao
1. Hàm số y=ax2
Biết vẽ đồ thị và tính giá trị của hàm số.
Số câu
Số điểm
1
 1
1
 1
2.Phương trình bậc hai 1 ẩn
Biết giải PT bậc hai 1 ẩn và PT trùng phương.
Hiểu được cách thay m vào PT để giải PT và tìm điều kiện để PT có 2 nghiệm phân biệt.
Vận dụng được tìm điều kiện để PT có nghiệm thỏa mãn điều kiện.
Vận dụng giải được bài toán bằng cách lập phương trình.
Số câu
Số điểm
2
 2
2
 2
1
 1
1
 1 
6
 6
3. Góc với đường tròn
Hiểu được cách chứng minh tứ giác nội tiếp.
Vận dụng tứ giác nội tiếp để chứng minh tia phân giác của góc.
Số câu
Số điểm
1
 1
1
 1
2
 2
4.Hình trụ
Hiểu được công thức để tính diện tích và thể tích của hình trụ.
Số câu
Số điểm
2
 1
2
 1
Tổng số câu
Tổng số điểm
Tỉ lệ %
 3 
 3
 30%
 5 
 4
 40%
 2 
 2 
 20%
 1
 1
 10% 
11
 10 
 100% 
 ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KỲ II
 Năm học: 2014-2015
 Môn thi: Toán- Lớp 9
 Thời gian: 90 phút( không kể phát đề)
Câu 1. ( 1,0 điểm) Cho hàm số y = f(x) = x2 
Vẽ đồ thị của hàm số trên.
Tính f(1,5) ; f(-8)
Câu 2: ( 2,0điểm ) Giải các phương trình sau: 
x2 - 7x + 12 = 0 
x4 + 3x2 - 4 = 0 
Câu 3: (3,0 điểm)
 Cho phương trình bậc hai: (1)
 a) Giải phương trình (1) khi m =1.
 b) Tìm giá trị của m để phương trình (1) có 2 nghiệm phân biệt.
 c) Gọi x1, x2 là hai nghiệm của phương trình (1). Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn x12 + x22 = 10.
Câu 4: (1,0 điểm) Giải bài toán sau:
Một xe khách và một xe du lịch khởi hành cùng một lúc từ A đến B. Xe du lịch có vận tốc lớn hơn vận tốc của xe khách là 20 km/h, do đó nó đến B trước xe khách 25 phút. Tính vận tốc của mỗi xe, biết khoảng cách AB là 100 km. 
Câu 5: (2,0 điểm) Cho tứ giác ABCD nội tiếp trong nửa đường tròn tâm O đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD tại F. Chứng minh rằng:
	a) Tứ giác DCEF nội tiếp.
 	b) Tia CA là tia phân giác của .
Cậu 6: (1,0 điểm) Một hình trụ có bán kính đường tròn đáy là 6cm, chiều cao 9cm. Hãy tính: 
	a) Diện tích xung quanh của hình trụ.
b) Thể tích của hình trụ.
 (Cho biết 3,14)
Hết
 ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
 Môn: Toán lớp 9-Học kỳ II
 Năm học: 2014-2015
Câu
 Đáp án
 Điểm
Câu 1
a) HS lập bảng đúng
 Vẽ đồ thị đúng
b) f(1,5) = 2,25
 f(-8) = 64
0,25 
0,25
0,25
0,25
Câu 2
 a) Tính đúng D = 1
 Tính đúng hai nghiệm x1 = 4, x2 = 3 
b) 
Đặt x2 = t (ĐK t≥0)
Ta có PT : t2 + 3t - 4 = 0
Có dạng: a + b + c = 1 +3+(-4) = 0 
 t1 = 1 ; t2 = -4 (loại)
Với t = 1 x1 = 1, x2 = -1
Vậy Phương trình đã cho có 2 nghiệm: x1 = 1; x2 = –1
0,5
0,25 – 0,25
0,25
0,25
0,25
0,25
Câu 3
a. Khi m=1 ta có phương trình: 
 Phương trình có dạng a-b+c = 2 + ( -3) + 1 = 0
 Vậy phương trình có 2 nghiệm: 
b. Ta có: 
Phương trình có 2 nghiệm phân biệt khi
Hay 9 - 8m > 0 
Vậy với thì PT có 2 nghiệm phân biệt
c) Vì x1 , x2 là 2 nghiệm của PT. Áp dụng hệ thức Vi – ét ta có:
 x1 + x2 = 
 x1 . x2 = 
Vì x12 + x22 = 10
ó (x1 + x2 ) 2 – 2 x1.x2 = 10
ó 
ó m = - 
Vậy m = - thì phương trình có 2 nghiệm x1, x2 thỏa mãn 
điều kiện x12 + x22 = 10 
0,25
0,25
0,25 – 0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Câu 4
Gọi vận tốc của xe khách là x (km/h) ĐK: x > 0 
 Vận tốc của xe du lịch là x + 20 (km/h)
Thời gian đi từ A đến B của xe khách là : (giờ)
Thời gian đi từ A đến B của xe du lịch là : (giờ)
Vì xe du lịch đến B trước xe khách 25 phút = giờ 
nên ta có phương trình: -= 
=> x1 = 60 ( nhận )
 x2 = -80 < 0 ( loại )
 Vậy: vận tốc của xe khách là: 60 km/h; 
 vận tốc của xe du lịch là: 60 + 20 = 80 (km/h)
0,25
0,25
0,25
0,25
Câu 5
O
a)Ta có = 900 ( góc nội tiếp chắn nửa đường tròn đường kính AD ) 
Xét tứ giác DCEF có: 
 = 900 ( cm trên )
 = 900 ( vì EF ^ AD (gt) )
=>+ = 1800 ( tổng hai góc đối )
 => Tứ giác DCEF là tứ giác nội tiếp.
b) Vì tứ giác DCEF là tứ giác nội tiếp ( cm câu a ) 
 => ( góc nội tiếp cùng chắn cung EF ) (1)
 Mà: (góc nội tiếp cùng chắn cung AB ) (2)
Từ (1) và (2) => 
 Vậy CA là tia phân giác của .
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Câu 6
a) Diện tích xung quanh của hình trụ là: 
Sxq = 2rh 
 = 2.3,14.6.9 = 339,12 (cm2)
b) Thể tích của hình trụ là: 
V = r2h 
 = 3,14 . 62 . 9 = 1017,36 (cm3)
0,25
0,25
0,25
0,25
Ghi chú: - Học sinh có lời giải khác mà đúng vẫn đạt điểm tối đa
 - Câu 5 học sinh không vẽ hình hoặc vẽ hình sai thì không chấm điểm.