Đề (đề nghị) kiểm tra học kỳ 2 năm học 2015-2016 môn Toán lớp 9 - Trường THCS Độc Lập

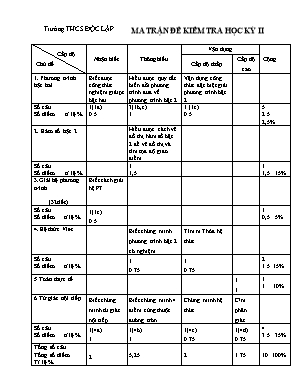
Trường THCS ĐỘC LẬP 	MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II
 Cấp độ
 Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
 Cộng
Cấp độ thấp
Cấp độ cao
1. Phương trình bậc hai
Biết được công thức nghiệm giảipt bậc hai
Hiểu được quy tắc biến đổi phương trình đưa về phương trình bậc 2
Vận dụng công thức đặc biệt giải phương trình bậc 2
Số câu
Số điểm tỉ lệ %
1(1a)
0.5
3(1b,c)
1
1 (1e) 
0.5
5 
2.5 2,5% 
2. Hàm số bậc 2
Hiểu được cách vẽ đồ thị hàm số bậc 2 để vẽ đồ thị và tìm tọa độ giao điểm
Số câu
Số điểm tỉ lệ %
1
1,5
1
1,5 15%
3.Giải hệ phương trình 
(32tiết)
Biết cách giải hệ PT
Số câu
Số điểm tỉ lệ %
1(1c)
0.5
1
0,5 5%
4.Hệ thức Viet 
Biết chứng minh phương trình bậc 2 có nghiệm
Tìm m Thỏa hệ thức
Số câu
Số điểm tỉ lệ %
1
0.75
1
0.75
2
1.5 15%
5 Toán thực tế
1
1
1
1 10%
6 Tứ giác nội tiếp
Biết chứng minh tứ giác nội tiếp 
Biết chứng minh 4 điểm cùng thuộc đường trón 
Chứng minh hệ thức 
C/m phân giác 
Số câu
Số điểm tỉ lệ %
1(4a)
1
1(4b)
1
1(4c)
0.75
1(4d)
0.75
4
3.5 35%
Tổng số câu
Tổng số điểm 
Tỉ lệ % 
2
5,25
2
1.75
10 100%
Phòng Giáo Dục – Đào Tạo Quận Phú Nhuận 
Trường THCS ĐỘC LẬP 
ĐỀ(ĐỀ NGHỊ) KIỂM TRA HỌC KỲ 2 NĂM HỌC 2015-2016
MÔN TOÁN LỚP 9
Thời gian làm bài : 90 phút
Bài 1 (2.5 điểm)
Giải các phương trình và hệ phương trình:
x2 -7x = -12
x2 (x2 - 9 ) = -20
x4 + 2x2 -15 =0
x2 – ( +1)x + = 0
Bài 2 (1,5 điểm)
Cho hàm số: y = x2 (P) và (D) : y = x + 2 
Vẽ đồ thị (P) và (D) trên cùng hệ trục tọa độ 
Tìm tọa độ giao điểm của (P) và (D)
Bài 3 (1.5 điểm)
Cho phương trình: x2 – (4m -1)x - 4m = 0 	( x là ẩn số)
Chứng minh phương trình luôn có hai nghiệm x1, x2 với mọi giá trị của m
Tính tổng và tích của hai nghiệm của phương trình theo m.
Gọi x1, x2 là 2 nghiệm của phương trình , tìm m để: 
Bài 4 (3,5 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng:
Tứ giác CEHD, nội tiếp .
Bốn điểm B,C,E,F cùng nằm trên một đường tròn.
AE.AC = AH.AD; AD.BC = BE.AC.
H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.
Bài 5 (1 điểm) Bác Phương vay vốn ngân hàng 2.000.000 đồng để làm kinh tế gia đình trong kỳ hạn một năm ,đến cuối năm, Bác Phương được ngân hàng cho vay thêm một năm nữa .Đến cuối năm thứ 2 ,Bác phải trả số tiền là 2.420.000 đồng . Hỏi lãi suất ngân hàng là bao nhiêu phần trăm /1 năm ?
Giáo Viên : Võ Thị Thanh Hà
Đáp án 
Bài 1 (2.5đ) : 
 a) = 1	 0.25
 x1 = 4 , x2 = 3	 0.25
Thu gọn pt: t1 =5;t2=4 (0.25) 	 0.25
 x1, x2 0.25
 c)
 0.25x2
 d) 0.25x2
	e) a+b+c = 0 (0.25) suy ra : x1 = 1 ; x2 = (0.25)
Bài 2 (1.5đ) : 
 a) Bảng giá trị và đồ thị đúng 0.5x2
 b) Tìm tọa độ giao điểm 0.25x2
Bài 3 (1.5đ) :
 a) (0.25) với mọi m (0.25) suy ra PT luôn có 2 nghiệm (0.25) b) 
 0.25 c) (0.25) suy ra : m=-1 hay m=3/4 (0.25) 
Bài 4 (3.5đ) : 
Xét tứ giác CEHD ta có:
Ð CEH = 900 ( Vì BE là đường cao) 0.25
Ð CDH = 900 ( Vì AD là đường cao) 0.25
=> Ð CEH + Ð CDH = 1800
 Mà Ð CEH và Ð CDH là hai góc đối của tứ giác CEHD 0.25
 Do đó CEHD là tứ giác nội tiếp 0.25
Theo giả thiết: BE là đường cao => BE ^ AC => ÐBEC = 900. 0.25
CF là đường cao => CF ^ AB => ÐBFC = 900. 0.25
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC. 0.25
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn. 0.25
Xét hai tam giác AEH và ADC ta có: Ð AEH = Ð ADC = 900 ; Â là góc chung 
=> D AEH ~ DADC 0.25 => => AE.AC = AH.AD. 0.25
* Xét hai tam giác BEC và ADC ta có: Ð BEC = Ð ADC = 900 ; ÐC là góc chung 
=> D BEC ~ DADC => => AD.BC = BE.AC. 0.25
4. Ta có ÐC1 = ÐA1 ( vì cùng phụ với góc ABC)
ÐC2 = ÐA1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> ÐC1 = Ð C2 => CB là tia phân giác của góc HCM; lại có CB ^ HM => D CHM cân tại C 
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
 Theo chứng minh trên bốn điểm B,C,E,F cùng nằm trên một đường tròn
 => ÐC1 = ÐE1 ( vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp 
ÐC1 = ÐE2 ( vì là hai góc nội tiếp cùng chắn cung HD)
ÐE1 = ÐE2 => EB là tia phân giác của góc FED. 0.25
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE (0.25) mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF. (0.25)
	Bài 5 : 1điểm
Biểu thị qua x số tiền phải trả sau năm thứ 1 : 0.25
Lập phương trình : 0.25
Giải phương trình : 0.25
Kết luận lãi suất là : 10% (0.25)