Đề (đa) kiểm tra toán giữa học kì II năm học: 2015 - 2016

ĐỀ (ĐA) KIỂM TRA TOÁN GIỮA HỌC KÌ II
Năm học: 2015-2016
Bài 1: (2 điểm)	
Giải phương trình và hệ phương trình sau:
a) 	b) x2 - 4x + 3 = 0
Giải
a/ thay y = 1 – x vào PT 1 có: 3x + 2 – 2x =1è x = –1; y = 2
b/ PTbậc 2 có dạng a+b+c=0 x1 = 1; x2 = 3 è S={1; 3}
 Bài 2:(2,5 điểm)
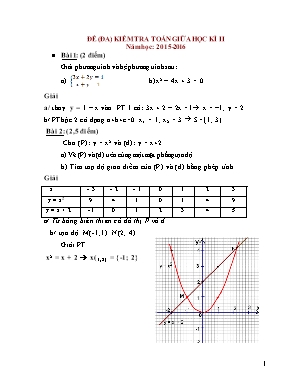
 Cho (P): y = x2 và (d): y = x+2 
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ.
b) Tìm toạ độ giao điểm của (P) và (d) bằng phép tính.
Giải
 x 
- 3
- 2
- 1
0
1
2
3
 y = x2
9
4
1
0
1
4
9
 y = x + 2
-1
0
1
2
3
4
5
a/ Từ bảng biến thiên có đồ thị P và d
 b/ tọa độ M(-1;1) N(2; 4)
 Giải PT 
 x2 = x + 2 è x(1;2) = {-1; 2}
Bài 3:(2 điểm) 
Một ô tô dự định đi từ A đến B với vận tốc đã định. Nếu ô tô đó tăng vận tốc thêm 10km mỗi giờ thì đến B sớm hơn dự định 1 giờ 24 phút , nếu ô tô giảm vận tốc đi 5 km mỗi giờ thì đến B muộn hơn 1 giờ. Tính độ dài quãng đường AB và vận tốc dự định.
Giải
Gọi x là quãng đường AB, v0 là vận tốc dự định; t0 là thời gian DĐ thì x = v0 x t0 [*] ; Theo đề ta có:
 (v0 + 10)(t0 – 1,4) = (v0 – 5)(t0 + 1) [**]
Giải PT [*] và [**] tính ra x= 280; v0 = 40
 è ĐS: quãng đường AB là 280km, vận tốc dự định là 40 km/h
Bài 4. (3 điểm) 
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng:
Các tứ giác AEHF, BCEF nội tiếp .
AE.AC = AH.AD; AD.BC = BE.AC.
H và M đối xứng nhau qua BC.
Giải
a/ Tứ giác AEHF có ÐE = ÐF = 90o Þ AEHF là tứ giác nội tiếp
Tứ giác BCEF có 2 góc vuông BEC và BFC cùng chắn BC ÞBCER là tứ giác nội tiếp
b/ Từ các cặp tam giác vuông đồng dạng suy ra: AE.AC = AH.AD; AD.BC = BE.AC
c/ Xét tam giác CHM chứng minh được
C1 = A1; C2 = A1 (cùng chắn cung bằng nhau)
Þ CD vừa là phân giác vừa là đường cao
Þ tam giác CHM cân Þ CD vừa là trung trực của HM
 è Vậy H và M đối xứng nhau qua BC (ĐPCM
Bài 5. (0.5 điểm) 
Cho phương trình: 
 (m - 1)x2 – 2(m+1)x+ m – 2 = 0 (1) (m là tham số).
Tìm giá trị của m để phương trình (1) có hai nghiệm phân biệt.
Giải
Điều kiện để phương trình (1) có hai nghiệm phân biệt là: 
PT (1) là PT bậc 2 có hệ số b chẵn nên chỉ cần điều kiên ∆’ > 0
 ∆’ = (m + 1)2 – (m – 1) (m – 2) 
 è ĐS: với m > 1/5 thì PT (1) có 2 nghiệm phân biệt. 
PHH sưu tầm đề & soạn bài giải 3/2016
nguồn vndoc.com
TRƯỜNG THCS CAO DƯƠNG