Đề cương ôn tập toán 9 – học kì 1 – năm học: 2015 – 2016

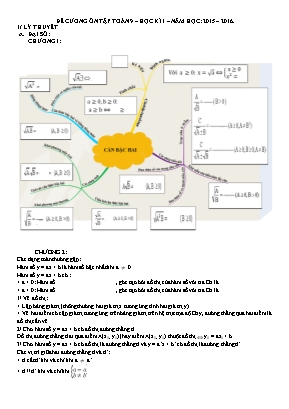
ĐỀ CƯƠNG ÔN TẬP TOÁN 9 – HỌC KÌ 1 – NĂM HỌC: 2015 – 2016.
1/ LÝ THUYẾT
ĐẠI SỐ:
CHƯƠNG 1:
	CHƯƠNG 2:
Các dạng toán thường gặp:
Hàm số y = ax + b là hàm số bậc nhất khi a ≠ 0.
Hàm số y = ax + b có :
+ a > 0: Hàm số ., góc tạo bởi đồ thị của hàm số với tia Ox là ...
+ a < 0: Hàm số ., góc tạo bởi đồ thị của hàm số với tia Ox là .
1/ Vẽ đồ thị:
+ Lập bảng giá trị (thông thường hai giá trị x tương ứng tính hai giá trị y)
+ Vẽ hai điểm có cặp giá trị tương ứng trên bảng giá trị trên hệ trục tọa độ Oxy, đường thẳng qua hai điểm là đồ thị cần vẽ.
2/ Cho hàm số y = ax + b có đồ thị đường thẳng d.
Đồ thị đường thẳng d đi qua điểm A(x0; y0) (hay điểm A(x0; y0) thuộc đồ thị ⇔ y0 = ax0 + b.
3/ Cho hàm số y = ax + b có đồ thị là đường thẳng d và y = a’x + b’ có đồ thị là đường thẳng d’.
Các vị trí giữa hai đường thẳng d và d’:
+ d cắt d’ khi và chỉ khi a ≠ a’.
+ d // d’ khi và chỉ khi a=a'b≠b'
+ d trùng d’ khi và chỉ khi a=a'b=b'
+ d vuông góc với d’ khi và chỉ khi a . a’ = - 1. 
Tìm tọa độ giao điểm của hai đường thẳng d và d’:
Hoành độ giao điểm của hai đường thẳng d và d’ là nghiệm của phương trình ax + b = a’x + b’.
Giải phương trình hoành độ giao điểm tìm x = x0 , thay vào một trong hai hàm số tính y = y0.
Tọa độ giao điểm của hai đường thẳng là (x0; y0).
4/ Viết phương trình đường thẳng:
Viết phương trình đường thẳng đi qua hai điểm A(xA; yA), B(xB; yB).
+ Thay tọa độ hai điểm A, B vào đường thẳng y = ax + b ta được hệ phương trình.
+ Giải hệ phương trình ta tìm được a = a0, b = b0 .
+ Kết luận; Phương trình đường thẳng đi qua hai điểm A, B là y = a0x + b0.
5/ Điều kiện để d và d’ cắt nhau tại một điểm nằm trên trục tung là a ≠ a’, b = b’.
6/ Điều kiện để d và d’ cắt nhau tại một điểm nằm trên trục hoành là a ≠ a’, ba=b'a'.
7/ Tìm điều kiện để d và d’ cắt nhau tại một điểm có hoành độ là m:
+ B1: Tìm điều kiện để a ≠ a’.
+ B2: Thay x = m vào d (hoặc d’) tìm y = y0.
+ B3: Thay x = m và y = y0 vào đường thẳng còn lại, kết hợp với điều kiện B 1 để kết luận.
8/ Tìm điều kiện để d và d’ cắt nhau tại một điểm có tung độ là m:
+ B1: Tìm điều kiện để a ≠ a’.
+ B2: Thay y = m vào d (hoặc d’) tìm x = x0.
+ B3: Thay y = m và x = x0 vào đường thẳng còn lại, kết hợp với điều kiện B 1 để kết luận.
HÌNH HỌC:
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG.
TỈ SỐ LƯỢNG GIÁC CỦA HAI GÓC NHỌN PHỤ NHAU.
Trong tam giác ABC vuông tại A, B+C= 900
ĐƯỜNG TRÒN
+ Qua ba điểm không thẳng hàng ta vẽ được  đường tròn.
+ Nếu tam giác ABC vuông tại A thì A, B, C thuộc đường tròn tâm I là .. BC (cạnh huyền)
+ Nếu một tam giác nội tiếp đường tròn và có một cạnh là đường kính của đường tròn thì 
...
+ Trong một đường tròn:
Trong các dây thì dây lớn nhất là đường kính.
Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Đường kình đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây.
Hai dây bằng nhau thì .. tâm.
Hai dây cách đều tâm thì .
Dây nào ... thì dây đó gần tâm hơn.
Dây nào..tâm hơn thì dây đó lớn hơn.
+ Vị trí tương đối của đường thẳng với đường tròn: 
Vị trí tương đối của đường thẳng và đường tròn.
Số điểm chung
Hệ thức giữa d và R.
Đường thẳng và đường tròn cắt nhau
d  R
....
1
d  R
Đường thẳng và đường tròn không giao nhau.
d  R
+ Đường thẳng cắt đường tròn tại 2 điểm gọi là 
+ Đường thẳng chỉ có một điểm chung với đường tròn gọi là ...... Điểm chung của 
+ Định lí dùng chứng minh một đường thẳng là tiếp tuyến của đường tròn:
Một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó 
bán kính đi qua tiếp điểm.
Một đường thẳng đi qua một điểm của..và .
với bán kính đi qua điểm đó thì đường thẳng ấy là .. của đường tròn.
+ Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
Điểm đó hai tiếp điểm.
Tia kẻ từ điểm đó đi qua tâm là của góc tạo bởi hai tiếp tuyến.
Tia kẻ từ tâm đi qua điểm đó là  của góc tạo bởi hai bán kính đi qua các tiếp điểm.
2/ BÀI TẬP:
Dạng 1: Liên quan đến căn thức:
Bài 1: Rút gọn các biểu thức sau: 
245-532+3128-500	ĐS: 42-45
548+227-3300	ĐS: -43
1100-744+2176-1331	ĐS: -711
68-554+3216-2200	ĐS: 36-82
272-450+5288-3128	ĐS: 282
324+254-7150+56	ĐS: -186
Bài 2: Rút gọn các biểu thức sau:
33-23+1+3-33-1	ĐS: 3+1
66-56+1+6-66-1	ĐS: 6+1
56-1-56+1	ĐS: 2
37-2+37+2	ĐS: 27
12-3-5+12+3+5	ĐS: 322
17-26+1-17+24-1	ĐS: 0
Bài 3: Rút gọn các biểu thức:
5+255+2+2+22+1:15-2	ĐS: 3
5+255+2+7+77+1:15-7	ĐS: - 2 
25+1-23-5	ĐS: - 1 
23-1-26-33	ĐS: 233
21-71-3+15-102-3:17-5	ĐS: -35-6
6+266+2-2+22+1:16+2	ĐS: 2-3
Bài 4: Rút gọn các biểu thức sau:
9-45-6-25	ĐS: -1
12-37-12+37	ĐS: - 6
23-610+13+410	ĐS: 52
6+25-13+48	ĐS: 3+1
12-63+4-23	ĐS: 2
6+104-15	ĐS: 2
12+85-26	ĐS: 2
Bài 5: Rút gọn biểu thức sau:
a-aa-2a+1+a+aa+2a+1 với a ≥ 0, a≠1.
a2-aa+a+1+a2+aa-a+1
x-2x+2-x+2x-2x-4x với x > 0, x ≠ 4.
a+3a-3-a+3a+3+23a:3a-3
2xx+3x+2+5x+1x+4x+3+x+10x+5x+6 với x > 0
xx-4+22-x+1x+2:x-2+10-xx+2 với x > 0 và x≠ 4.
Bài 6: Giải các phương trình sau:
4x+4+25x+25+2=18
18x+9+38x+4=3
4x2-20x+25=1
x2-9=3-x
x+3+2-x=3
25x2-30x+9=x+7
x-1+2x-2=2
x2-x+x2+x-2=0
Dạng 2: Hàm số bậc nhất (Xem lại các dạng bài trong phiếu bài tập cô đã giao)
Dạng 3: Hình học
Bài 1: Cho đường tròn tâm O, đường kính AB. Lấy điểm A giữa đoạn OA sao cho AE > EO. Gọi H là trung điểm AE, kẻ dây CD vuông góc với AB tại H. Đường thẳng DE cắt BC tại I.
Tứ giác ACED là hình gì?
Chứng minh: HI là tiếp tuyến của đường tròn đường kính EB.