Đáp án đề kiếm tra chất lượng cuối kì II - Thạch Thành - Thanh Hóa năm học: 2015 - 2016 môn: Toán 7

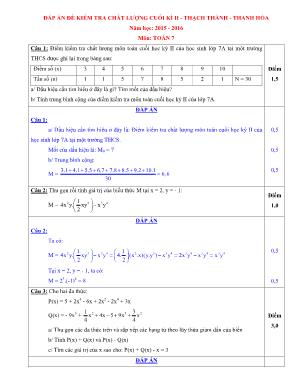
ĐÁP ÁN ĐỀ KIẾM TRA CHẤT LƯỢNG CUỐI KÌ II - THẠCH THÀNH - THANH HÓA 
Năm học: 2015 - 2016 
Môn: TOÁN 7 
Câu 1: Điểm kiểm tra chất lượng môn toán cuối học kỳ II của học sinh lớp 7A tại một trường 
THCS được ghi lại trong bảng sau: 
Điểm số (x) 3 4 5 6 7 8 9 10 
Tần số (n) 1 1 5 7 8 5 2 1 N = 30 
a/ Dấu hiệu cần tìm hiểu ở đây là gì? Tìm mốt của dấu hiệu? 
b/ Tính trung bình cộng của điểm kiểm tra môn toán cuối học kỳ II của lớp 7A. 
Điểm 
1,5 
ĐÁP ÁN 
Câu 1: 
 a/ Dấu hiệu cần tìm hiểu ở đây là: Điểm kiểm tra chất lượng môn toán cuối học kỳ II của 
học sinh lớp 7A tại một trường THCS. 
 Mốt của dấu hiệu là: M0 = 7 
 b/ Trung bình cộng: 
 M = 
3.1 4.1 5.5 6.7 7.8 8.5 9.2 10.1
6,6
30
      
 
0,5 
0,5 
0,5 
Câu 2: Thu gọn rồi tính giá trị của biểu thức M tại x = 2, y = - 1: 
 M = 2 3 3 4
1
4x y. xy x y
2
 
 
 
Điểm 
1,0 
ĐÁP ÁN 
Câu 2: 
 Ta có: 
 M = 2 3 3 4 2 3 3 4 3 4 3 4 3 4
1 1
4x y. xy x y 4. (x .x)(y.y ) x y 2x y x y x y
2 2
   
        
   
 Tại x = 2, y = - 1, ta có: 
 M = 23.(-1)4 = 8 
0,5 
0,5 
Câu 3: Cho hai đa thức: 
 P(x) = 5 + 2x4 - 6x + 2x2 - 2x4 + 3x 
 Q(x) = - 9x3 + 2 3 2
1 3
x 4x 5 9x x
4 4
    
 a/ Thu gọn các đa thức trên và sắp xếp các hạng tử theo lũy thừa giảm dần của biến 
 b/ Tính P(x) + Q(x) và P(x) - Q(x) 
 c/ Tìm các giá trị của x sao cho: P(x) + Q(x) - x = 3 
Điểm 
3,0 
ĐÁP ÁN 
E2
1
M
K
I
A B
C
D
Câu 3: 
 a/ Thu gọn và sắp xếp: 
 P(x) = 5 + 2x4 - 6x + 2x2 - 2x4 + 3x = (2x4 - 2x4) + 2x2 + (-6x + 3x) + 5 = 2x2 - 3x + 5 
 Vậy: P(x) = 2x2 - 3x + 5 
 Q(x) = -9x3+ 2 3 2 3 3 2 2 2
1 3 1 3
x 4x 5 9x x ( 9 x 9x ) x x 4x 5 x 4x 5
4 4 4 4
 
              
 
 Vậy: Q(x) = 2x 4x 5  
 b/ Tính: P(x) = 2x2 - 3x + 5 P(x) = 2x2 - 3x + 5 
 Q(x) = 2x 4x 5  Q(x) = 2x 4x 5  
 P(x) + Q(x) = 3x2 + x P(x) - Q(x) = x2 - 7x + 10 
 c/ Ta có: 
 P(x) + Q(x) - x = 3 
  3x2 + x - x = 3 
  3x2 = 3 
  x2 = 1 
  x =  1 
0,5 
0,5 
1,0 
0,5 
0,5 
Câu 4: Cho ABC vuông tại A, đường phân giác CD (DAB), kẻ DE vuông góc với BC 
(EBC). Gọi I là giao điểm của AE và CD. 
 a/ Chứng minh AC = EC 
 b/ Chứng minh CI  AE và EI < BD 
 c/ Từ B kẻ đường thẳng vuông góc với CD và cắt đường thẳng CD tại K. Chứng minh 3 
đường thẳng AC, DE, BK đồng quy. 
Điểm 
3,5 
ĐÁP ÁN 
Câu 4: 
GT 
ABC,  0A 90 ,  1 2C C , DE BC ,  I AE CD  , 
BK CD . 
KL 
a/ AC = EC 
b/ CI  AE và EI < BD 
c/ AC, DE, BK đồng quy 
 a/ Xét 2 tam giác vuông ACD và EDC có: 
 CD: Cạnh chung 
  1 2C C (GT) 
  ACD = EDC (Cạnh huyền - góc nhọn) 
  AC = EC (hai cạnh tương ứng) 
0,5 
0,5 
0,5 
 b/ Vì AC = EC (Theo câu a) nên ACE cân tại C, ACE cân tại C có đường phân giác CI 
CI cũng là đường cao  CI  AE. 
 Trong tam giác vuông IDE có IE < ED (Vì ED là cạnh huyền) (1) 
 Trong tam giác vuông DEB có ED < BD (Vì BD là cạnh huyền) (2) 
 Từ (1) và (2)  IE < BD. 
 c/ Giả sử AC và BK cắt nhau tại M, ta sẽ chứng minh DE cũng đi qua M, thật vậy: 
 Trong CMB có CK, BA là hai đường cao mà  D CK BA  D là trực tâm của 
CMB MD BC mà DE BC 3 điểm M, D, E cùng thuộc một đường thẳng hay DE đi 
qua M. Vậy AC, DE, BK đồng quy. 
0,5 
0,5 
0,5 
0,5 
Câu 5: Cho đa thức F(x) thỏa mãn: (x - 1).F(x) = (x + 4).F(x + 8) với mọi x. Chứng minh rằng đa 
thức F(x) có ít nhất 2 nghiệm. 
Điểm 
1,0 
ĐÁP ÁN 
Câu 5: 
*) Khi x = - 4, ta có: 
 (- 4 - 1).F(- 4) = (- 4 + 4).F(- 4 + 8) 
 - 5.F(- 4) = 0.F(4) 
 - 5.F(- 4) = 0 
 F(- 4) = 0 
 Vậy - 4 là một nghiệm của F(x) 
*) Khi x = 1, ta có: 
 (1 - 1).F(1) = (1 + 4).F(1 + 8) 
 0.F(1) = 5.F(9) 
 5.F(9) = 0 
 F(9) = 0 
 Vậy 9 là một nghiệm của F(x) 
 Vậy F(x) có ít nhất 2 nghiệm là - 4 hoặc 9 
0,25 
0,5 
Thầy Hải - 0983 022 058