Câu hỏi kiểm tra học kì 2 môn: Toán lớp 9

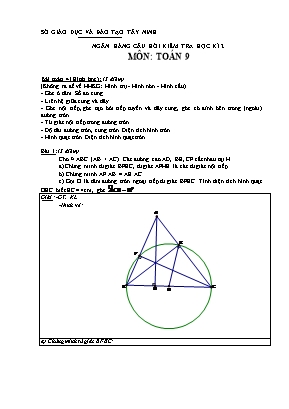
SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH
NGÂN HÀNG CÂU HỎI KIỂM TRA HỌC KÌ 2
MƠN: TỐN 9
Bài tốn 4 (Hình học): (3 điểm)
(Khơng ra đề về HHKG: Hình trụ - Hình nĩn - Hình cầu)
- Gĩc ở tâm. Số đo cung.
- Liên hệ giữa cung và dây.
- Gĩc nội tiếp, gĩc tạo bởi tiếp tuyến và dây cung, gĩc cĩ đỉnh bên trong (ngồi) đường trịn.
- Tứ giác nội tiếp trong đường trịn.
- Độ dài đường trịn, cung trịn. Diện tích hình trịn.
- Hình quạt trịn. Diện tích hình quạt trịn.
Bài 1: (3 điểm)
Cho D ABC (AB < AC). Các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh tứ giác BFEC, tứ giác AFHE là các tứ giác nội tiếp.
b) Chứng minh AF.AB = AE.AC
c) Gọi O là tâm đường trịn ngoại tiếp tứ giác BFEC. Tính diện tích hình quạt OEC biết EC = 4cm, gĩc . 
Giải: -GT, KL
-Hình vẽ: 
a) Chứng minh tứ giác BFEC:
b) Vì tứ giác BFEC nội tiếp Þ 
mà nên 
lại cĩ gĩc A chung do đĩ DAEF D ACB ( g.g) 
Þ AF.AB = AE.AC
c) Tam giác OEC cĩ: OE = OC = R Þ DOEC cân mà Þ DOEC đều 
Þ Þ n = 600
Bài 2: (3 điểm)
Tam giác ABC cân tại A cĩ cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường trịn (0). Tiếp tuyến tại B và C của đường trịn lần lượt cắt tia AC và tia AB ở D và E. chứng minh: 
a) BD2 = AD.CD
b) Tứ giác BCDE là tứ giác nội tiếp.
c) BC song song với DE.
Giải: - GT,KL:
- Hình vẽ: 
a) BD2 = AD.CD
Hai tam giác ABD và BCD cĩ: 
(cùng bằng )
 chung
nên DABD ~ DBCD (g.g)
b) Tứ giác BCDE là tứ giác nội tiếp
Ta cĩ : (gĩc cĩ đỉnh bên ngồi đường trịn)
 (gĩc cĩ đỉnh bên ngồi đường trịn)
Mà AB = AC (DABC cân tại A) 
Do đĩ 
D và E cùng nhìn BC dưới một gĩc bằng nhau.
Suy ra bốn điểm B, C, D, E cùng nằm trên một đường trịn hay tứ giác BCDE là tứ giác nội tiếp.
c) BC song song với DE
Ta cĩ (DABC cân tại A)
 (hai gĩc kề bù)
mà (tổng 2 gĩc đối của tứ giác nội tiếp)
Do đĩ : (cùng bù với )
Hay 
Mà ở vị trí đồng vị nên BC // ED.
Bài 3: (3 điểm)
Cho tam giác ABC vuơng tại A cĩ . Kẻ đường cao AH và lấy trên đoạn HC một điểm D sao cho HD = HB, qua C kẻ đường thẳng vuơng gĩc với đường thẳng AD tại E. Chứng minh: 
a) Tứ giác AHEC nội tiếp được trong một đường trịn. Xác định tâm I của đường trịn đĩ.
b) r AHE là tam giác cân.
c) CB là tia phân giác của gĩc ACE .
Giải: - GT,KL:
- Hình vẽ: 
a) Xét tứ giác AHEC cĩ 
AH BC (gt)
AE EC (gt)
Do đĩ: Tứ giác AHEC nội tiếp .
Hai điểm H và E cùng nhìn AC cố định dưới một gĩc vuơng nên tâm I của đường trịn ngoại tiếp là trung điểm của AC.
b) Tam giác ABD cĩ AH vừa là đường cao vừa là đường trung tuyến 
 ABD cân tại A 
 AH cũng là đường phân giác của gĩc BAD
 (1)
Ta cĩ BA ^ AC BA là tiếp tuyến của đường trịn tâm I
 ( Cùng bằng ) (2)
Từ (1) và (2) HAE cân tại H
c) Ta cĩ HAE cân tại H HA =HE 
 ( Gĩc nội tiếp chắn các cung HA và cung HE)
 CB là tia phân giác của gĩc ACE.
Bài 4: (3 điểm)
Cho tam giác ABC vuơng ở A (AB < AC). Trên cạnh AC lấy một điểm M và vẽ đường trịn tâm O đường kính MC. Kẻ BM cắt đường trịn tại D. Đường thẳng DA cắt đường trịn tại S. 
a) Chứng minh ABCD là một tứ giác nội tiếp.
b) Chứng minh 
c) Chứng minh CA là tia phân giác của gĩc SCB.
Giải: -GT, KL
-Hình vẽ: 
a) Ta cĩ (gt)
 (gĩc nội tiếp chắn nửa đường trịn)
A và D cùng nhìn BC cố định dưới một gĩc 900.
Vậy A và D cùng nằm trên đường trịn đường kính BC hay tứ giác ABCD là tứ giác nội tiếp đường trịn đường kính BC.
b) Xét đường trịn đường kính BC.
Ta cĩ: (gĩc nội tiếp chắn cung AD)
 (gĩc nội tiếp chắn cung AD)
c) - Xét đường trịn đường kính BC:
Ta cĩ: (cùng chắn cung nhỏ AB) (1)
 - Xét đường trịn đường kính MC:
Ta cĩ: (cùng chắn cung nhỏ MS).
 Hay (2)
 Từ (1), (2) suy ra . Hay CA là tia phân giác 
Bài 5: (3 điểm)
Cho đường tròn (O; R) và một điểm A nằm ngồi đường trịn. Từ A vẽ hai tiếp tuyến AB, AC với (O) (B,C là các tiếp điểm). AO cắt BC tại H
a/ Chứng minh tứ giác ABOC nợi tiếp.
b/ Chứng minh AO ^ BC tại H.
c/ Từ B vẽ đường thẳng song song với AC, cắt đường tròn (O) tại D (khác điểm B). Đường thẳng AD cắt đường tròn (O) tại E (khác điểm D). Chứng minh: BC. EC = AC. BE 
Giải: - GT,KL:
- Hình vẽ: 
a/ Ta có:
OB ^ AB ( Tính chất của tiếp tuyến) 
OC ^ AC ( Tính chất của tiếp tuyến) 
Nên tứ giác ABOC nợi tiếp được trong một đường trịn
b/ Ta có:
AB = AC và (tính chất hai tiếp tuyến cắt nhau)
DABC cân tại A cĩ AH là phân giác nên cũng là đường cao 
Do đĩ AO ^ BC
c/ Xét DBCE và DCAE có:
 (cùng bằng )
 (vì cùng bằng )
Þ DBCE ~ DCAE (g-g)
Bài 6: (3 điểm)
Cho D ABC vuơng tại A, trung tuyến AD. Tia Cx nằm giữa hai tia CA và CB. Vẽ đường trịn (O) cĩ O thuộc AB, tiếp xúc với CB tại M, tiếp xúc với Cx tại N. Gọi E là giao điểm của AD và Cx. Chứng minh:
a) Tứ giác CANO nội tiếp.
b) Tia AO là tia phân giác của .
c) EA = EN
Giải: -GT, KL
-Hình vẽ: 
a) Ta cĩ (CN là tiếp tuyến của (O) )
 (gt)
Nên N, A cùng thuộc đường trịn đường kính CO
Þ Tứ giác CANO nội tiếp đường trịn đường kính CO
b) Ta cĩ nên M thuộc đường trịn đường kính CO
Trong đường trịn đường kính CO cĩ OM = ON
 (2 gĩc nội tiếp chắn hai cung bằng nhau)
Vậy AO là phân giác 
c) Ta cĩ (Tính chất trung tuyến thuộc cạnh huyền D ABC)
Þ D DAB cân tại D 
Mà (tính chất gĩc ngồi D MAB)
 (AO là phân giác )
Mặt khác: (2 gĩc nội tiếp cùng chắn cung )
Nên 
Þ D AEN cân tại E Þ EA = EN
Bài 7: (3 điểm)
Cho đường trịn (O,R) đường kính BC. A là điểm trên đường trịn sao cho 
AB = R, hạ AH^BC. Đường trịn tâm I, đường kính AH cắt AB, AC và đường trịn (O) tại D, E, F.
a/ Chứng minh tứ giác ADHE là hình chữ nhật.
b/ Chứng minh tứ giác BDEC nội tiếp.
c/ Chứng minh OA ^ DE.
d/ Tia AF cắt đường thẳng BC tại S. Chứng minh ba điểm S, D, E thẳng hàng.
Giải: - GT,KL:
- Hình vẽ: 
a/ c/m: ADHE là hình chữ nhật:
- Xét đường trịn đường kính BC:
 (gĩc nội tiếp chắn nửa đường trịn)
- Xét đường trịn đường kính AH:
 (gĩc nội tiếp chắn nửa đường trịn)
Tứ giác ADHE cĩ 3 gĩc vuơng nên là hình chữ nhật.
 b/ Ta cĩ : (gĩc nội tiếp cùng chắn cung của (I))
 (gĩc cĩ cạnh tương ứng vuơng gĩc)
Mà (hai gĩc kề bù)
Tứ giác BDEC nội tiếp được trong một đường trịn vì cĩ tổng số đo hai gĩc đối bằng 1800
c/ Vẽ đường kính AOM. Ta cĩ :
 (gĩc nội tiếp cùng chắn cung )
 (cùng bù với )
 (1)
Mà (gĩc nội tiếp chắn nửa đường trịn)
 (2)
Từ (1) và (2), suy ra 
Do đĩ DKAE (K là giao điểm của AO và DE) vuơng tại K
Hay tại K
Bài 8: (3 điểm)
Cho tam giác ABC vuơng tại A (AB < AC) và nội tiếp trong đường trịn tâm O, bán kính R. Gọi M là trung điểm của cạnh AC và AH là đường cao của tam giác ABC. 
a) Chứng minh tứ giác AMOH nội tiếp được trong một đường trịn. Xác định tâm I của đường trịn này. 
b) Đường trịn tâm I cắt AB tại N. Chứng minh 3 điểm M, I, N thẳng hàng. 
c) Cho AB = R. Tính theo R diện tích phần mặt phẳng giới hạn bởi cung nhỏ AC của đường trịn tâm O, cung AMO của đường trịn tâm I và đoạn OC. 
Giải: -GT, KL
-Hình vẽ:
a) Ta cĩ : (AH đường cao của ) (1)
M trung điểm của AC (giả thiết) (Đường kính đi qua trung điểm của 1 dây khơng qua tâm thì vuơng gĩc với dây ấy) hay (2)
Từ (1) và (2) ta cĩ 
Do đĩ tứ giác AMOH nội tiếp trong một đường trịn 
Vì nên tâm I của đường trịn ngoại tiếp tứ giác AMOH là trung điểm của đoạn OA
b) Chứng minh 3 điểm M , I , N thẳng hàng
Ta cĩ : A, M, N thuộc đường trịn tâm I 
Tam giác ABC vuơng tại A (giả thiết) 
MN là đường kính của đường trịn tâm I 
Vậy : M, I, N thẳng hàng 
c) * Diện tích hình quạt AOC :
Ta cĩ OA = OB = R và AB = R (giả thiết)
Þ DOAB đều Þ 
Do đĩ 
Nên 
* Tính diện tích nửa đường trịn tâm I:
* Diện tích cần tìm S = S1 – S2
 (đvdt)
Bài 9: (3 điểm)
Cho tam giác ABC nhọn nội tiếp đường trịn (O;R) . Các đường cao AD, BE, CF cắt nhau tại H . Vẽ tiếp tuyến của (O) .Chứng minh 
a) Tứ giác BFEC nội tiếp .
b) xx’// FE 
c) AB.AF = AC.AE
d) Cho biết sđ = 900 , bán kính R = 10cm . Tính độ dài cung nhỏ . 
Giải: -GT, KL
-Hình vẽ: 
a) Chứng minh tứ giác BFEC:
b) Ta cĩ : sđ
Tứ giác BFEC nội tiếp nên 
Þ (cùng bù với )
Þ // EF (2 gĩc ở vt so le trong )
c) DAEF và D ACB cĩ: (cm trên)
gĩc chung 
do đĩ DAEF D ACB ( g.g) 
Þ AF.AB = AE.AC
d) Vì sđ, R = 10cm nên 
Bài 10: (3 điểm)
Cho đường trịn (O) ; đường kính AB = 2R . Trên tia đối của tia BA lấy điểm C sao cho BC = R . Lấy điểm D thuộc đường trịn (O) sao cho BD = R , đường thẳng vuơng gĩc với AC tại C cắt AD tại N
a/ Chứng minh tứ giác BCND nội tiếp. 
b/ Chứng minh D ABN cân. 
c/ Tính diện tích hình quạt OBD của đường trịn (O) theo R . 
Giải: -GT, KL
-Hình vẽ: 
a) Xét đường trịn (O) cĩ gĩc ADB là gĩc nội tiếp chắn nửa đường trịn 
 nên (hai gĩc kề bù )
mà (gt)
Do đĩ: Tứ giác BCND cĩ tổng 2 gĩc đối bằng 1800 nên nội tiếp được trong 1 đường trịn
b) D ODB đều nên 
D ABD vuơng tại D Þ 
D ACN vuơng tại C cĩ 
- Tứ giác BCND nội tiếp cĩ BD = BC = R (gt) (2 gĩc nội tiếp chắn 2 cung bằng nhau ) 
tia NB nằm giữa ND và NC Þ
ÞD ABN cĩ ÞD ABN cân tại B 
c) Ta cĩ (D ODB đều)
Diện tích hình quạt : 
Bài 11: (3 điểm)
Cho DABC nhọn nội tiếp đường trịn (O; R). Vẽ 2 đường cao AH và BK, chúng cắt nhau tại D (điểm D khơng trùng với điểm O). 
a) Chứng minh: Tứ giác ABHK nội tiếp. 
b) Kẻ tiếp tuyến xCx’ với đường tròn (O) (C là tiếp điểm). Chứng minh: HK // xx’.
c) Cho = 1400 và R = 6 cm. Tính diện tích hình quạt trịn OAB ứng với cung nhỏ AB.
Giải: -GT, KL
-Hình vẽ: 
a) Chứng minh tứ giác ABHK:
b) Ta cĩ : sđ
Tứ giác ABHK nội tiếp nên 
Þ (cùng bù với )
Þ // HK (2 gĩc ở vt so le trong )
c) Ta cĩ (đối đỉnh)
Tứ giác CHDK cĩ : 
Mà là gĩc nội tiếp chắn cung 
 Þ n = 800
 hoặc S = 25,12 (cm2 )
Bài 12: (3 điểm)
Cho đường trịn tâm O đường kính AB. Trên đường trịn lấy điểm D khác A và B. Trên đường kính AB lấy điểm C và kẻ CH vuơng gĩc với AD (tại H). Đường phân giác trong của gĩc DAB cắt đường trịn tại E và cắt CH tại F. Đường thẳng DF cắt đường trịn tại N. Chứng minh rằng:
a) Gĩc ANF bằng ACF.
b) Tứ giác AFCN là tứ giác nội tiếp đường trịn.
c) Ba điểm C, N, E thẳng hàng.
Giải: -GT, KL
-Hình vẽ: 
a) Ta cĩ: BD^AD (Gĩc nội tiếp chắn ½ đường trịn)
CH^DD (gt)
Þ BD//CH
Do đĩ (hai gĩc đồng vị của hai đường thẳng song song)
Mà (hai gĩc nội tiếp cùng chắn 1 cung)
Vậy 
b) Ta cĩ (cm câu a)
Hai đỉnh N và C cùng nhìn đoạn AF dưới một gĩc khơng đổi 
Þ Tứ giác AFCN nội tiếp được trong đường trịn.
c) Tứ giác AFCN nội tiếp Þ (hai gĩc nội tiếp cùng chắn 1 cung)
ta cĩ: (gt)
Þ 
Mà (hai gĩc nội tiếp cùng chắn 1 cung của đường trịn (O) )
Do đĩ hay Ba điểm C, N, E thẳng hàng
Bài 13: (3 điểm)
Cho nửa đường trịn đường kính AB, từ B kẻ tiếp tuyến Bx với nửa đường trịn. C là một điểm trên nửa đường trịn, sao cho cung AC bằng cung CB. Trên cung CB lấy điểm D tùy ý (D khác C và B). Các tia AC, AD cắt Bx lần lượt tại E và F.
a) Chứng minh tam giác ABE vuơng cân.
b) Chứng minh tứ giác CEFD nội tiếp.
c) Khi C di động trên nửa đường trịn (C khác A và B) và D di động trên cung CB (D khác C và B). Chứng minh rằng AC.AE = AD.AF cĩ giá trị khơng đổi.
Giải: -GT, KL
-Hình vẽ: 
a) Chứng minh DABE vuơng cân:
Ta cĩ: (gĩc nội tiếp chắn nửa đường trịn)
 (do Bx là tiếp tuyến của (O) )
Do nên DACB cân (1)
Mà (2) (cùng phụ với )
Từ (1) và (2) 
Vậy DABE vuơng cân
b) Chứng minh tứ giác CEFD nội tiếp được.
Ta cĩ (cm trên).(1)
Mà (hai gĩc nội tiếp cùng chắn một cung). (2)
Từ (1) và (2) suy ra (3)
Mặt khác: (hai gĩc kề bù) (4)
Từ (3) và (4) suy ra: hay 
Suy ra tứ giác CEFD nội tiếp được.
c) Chứng minh AC.AE = AD.AF cĩ giá trị khơng đổi.
Xét DADC và DAEF cĩ:
 là gĩc chung
 (cm trên)
Vậy DADC ~ DAEF (gg)
 (5)
Xét tam giác vuơng ABF cĩ BD là đường cao thuộc cạnh huyền
 (R bán kính nửa đường trịn) (6)
Từ (5) và (6) suy ra AC.AE = AD.AF = 4R2 cĩ giá trị khơng đổi
Bài 14: (3 điểm)
Cho nửa đường trịn (O;R) đường kính BC và điểm A trên nửa đường trịn, M là một điểm trên cung nhỏ AC; tia BM cắt AC tại I, tia BA cắt tia CM tại D.
a) Chứng minh tứ giác AIMD nội tiếp.
b) Chứng minh: 
c) Giả sử: AB = R ; , Tính AD
Giải: -GT, KL
-Hình vẽ: 
a) Ta cĩ: (gĩc nội tiếp chắn nửa đường trịn (O) )
Nên (gĩc kề bù với gĩc vuơng)
Þ 
Vậy tứ giác ADMI nội tiếp được đường trịn đường kính ID
b) Tứ giác ADMI nội tiếp nên (hai gĩc nội tiếp cùng chắn 1 cung)
Mà (gĩc nội tiếp và gĩc ở tâm cùng chắn 1 cung)
Vậy 
c) Nếu AB = R ; ; Ta cĩ:
 (hai gĩc nội tiếp cùng chắn 1 cung)
Nên DADC vuơng cân tại A Þ AD = AC
Xét DABC vuơng tại A cĩ BC = 2R ; AB = R
Nên AC2 = BC2 – AB2 = 3R2 
Vậy 
Bài 15: (3 điểm)
Cho tứ giác ABCD nội tiếp đường trịn (O) cĩ S là điểm chính giữa cung AB. Gọi giao của SC, SD với AB lần lượt là E, F.
a) Chứng minh tứ giác CDFE nội tiếp;
b) Chứng minh SO là phân giác của gĩc ASB;
c) Gọi giao của DE, CF với (O) là M, N. Chứng minh SO vuơng gĩc với MN
Giải: -GT, KL
-Hình vẽ: 
a) Tứ giác CEFD cĩ:
Vậy 
Þ Tứ giác CEFD nội tiệp đường trịn
b) Xét DSAB cĩ:
SA = SB (Hai dây căng cung bằng nhau)
SO^AB (Đường kính đi qua điểm chính giữa cung)
Þ DSAB cân tại S cĩ SO là đường cao
Þ SO là phân giác 
c) Trong đường trịn ngoại tiếp tứ giác CEFD cĩ:
 (Hai gĩc nội tiếp cùng chắn một cung)
 (Hai cung chắn hai gĩc nội tiếp bằng nhau của (O) )
Þ SO^MN (Đường kính đi qua điểm chính giữa cung)
Bài 16: (3 điểm)
Giải: -GT, KL
-Hình vẽ: 
Bài 17: (3 điểm)
Giải: -GT, KL
-Hình vẽ: 
Bài 18: (3 điểm)
Giải: -GT, KL
-Hình vẽ: 
Bài 19: (3 điểm)
Giải: -GT, KL
-Hình vẽ: 
Bài 20: (3 điểm)
Giải: -GT, KL
-Hình vẽ: 
Bài 21: (3 điểm)
Giải: 
Bài 22: (3 điểm)
Giải: -GT, KL
-Hình vẽ: 
Bài 23: (3 điểm)
Giải: