Bài tập tự luận ôn tập Chương 4 Đại số 7

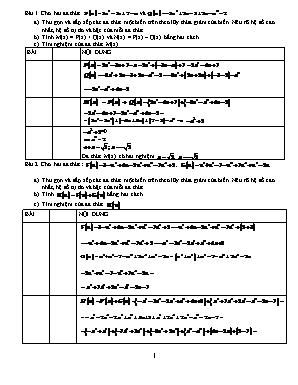
Bài 1. Cho hai đa thức và.
Thu gọn và sắp xếp các đa thức một biến trên theo lũy thừa giảm của biến. Nêu rõ hệ số cao nhất, hệ số tự do và bậc của mỗi đa thức.
Tính M(x) = P(x) + Q(x) và N(x) = P(x) – Q(x) bằng hai cách.
Tìm nghiệm của đa thức M(x).
BÀI
NỘI DUNG
= 
=0
Đa thức M(x) có hai nghiệm ; 
Bài 2. Cho hai đa thức: ; 
Thu gọn và sắp xếp các đa thức một biến trên theo lũy thừa giảm của biến. Nêu rõ hệ số cao nhất, hệ số tự do và bậc của mỗi đa thức.
Tính bằng hai cách.
Tìm nghiệm của đa thức 
BÀI
NỘI DUNG
Vậy đa thức có nghiệm 
Bài 3. Cho hai đa thức: 
Thu gọn và sắp xếp các đa thức một biến trên theo lũy thừa giảm của biến. Nêu rõ hệ số cao nhất, hệ số tự do và bậc của mỗi đa thức.
Tính bằng hai cách.
Tìm nghiệm của đa thức 
BÀI
NỘI DUNG
Vậy đa thức có nghiệm 
Bài 4. Cho hai đa thức sau: ; 
Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến. Tìm bậc, hệ số cao nhất, hệ số tự do của mỗi đa thức.
Tính P(x) – Q(x) bằng hai cách.
Chứng tỏ là nghiệm của P(x) nhưng không là nghiệm của Q(x)
Tính giá trị của P(x) – Q(x) tại .
BÀI
NỘI DUNG
1
a)
Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến. Tìm bậc, hệ số cao nhất, hệ số tự do của mỗi đa thức.
Vậy: 
Đa thức có bậc , hệ sồ cao nhất: , hệ số tự do: 
Vậy: 
Đa thức có bậc , hệ sồ cao nhất: , hệ số tự do: 
b)
Tính P(x) – Q(x) bằng hai cách.
c)
Chứng tỏ là nghiệm của đa thức , nhưng không phải là nghiệm của đa thức .
Với thì 
Vậy là nghiệm của đa thức 
Với thì 
Vậy không là nghiệm của đa thức 
d)
Tính giá trị của tại 
Thay vào 
Ta có: 
Vậy: Giá trị của đa thức là tại 
Bài 5. Cho hai đa thức : 
Sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm của biến. Tìm bậc, hệ số cao nhất, hệ số tự do của mỗi đa thức.
Tính bằng hai cách.
Chứng tỏ là nghiệm của đa thức , nhưng không phải là nghiệm của đa thức .
Tính giá trị của tại 
BÀI
NỘI DUNG
1
a)
Vậy: 
Đa thức có bậc 4, hệ sồ cao nhất: 3, hệ số tự do: 
Vậy: 
Đa thức có bậc 4, hệ sồ cao nhất: 3, hệ số tự do: 
b)
c)
Chứng tỏ là nghiệm của đa thức , nhưng không phải là nghiệm của đa thức .
Với thì 
Vậy là nghiệm của đa thức 
Với thì 
Vậy không là nghiệm của đa thức 
d)
Tính giá trị của tại 
Thay vào 
Ta có: 
Vậy: Giá trị của đa thức là tại 
Bài 6. Cho đa thức: 
Thu gọn và sắp xếp đa thức một biến trên theo lũy thừa giảm của biến. Nêu rõ hệ số cao nhất, hệ số tự do và bậc của mỗi đa thức.
Chứng tỏ đa thức Q(x) không có nghiệm 
BÀI
NỘI DUNG
a) Q(x) = x4 + 3x2 + 7
b) Vì x4 0 3x2 0 7 > 0 x4 + 3x2 + 7 > 0 Q(x) > 0 
KL.......
Bài 7. Cho đa thức: 
Thu gọn và sắp xếp đa thức một biến trên theo lũy thừa giảm của biến. Nêu rõ hệ số cao nhất, hệ số tự do và bậc của mỗi đa thức.
Chứng tỏ đa thức M(x) không có nghiệm 
BÀI
NỘI DUNG
M(x) = x4 + 2x2 + 5
Vì x4 0 2x2 0
 5 > 0 x4 + 2x2 + 5 > 0 M(x) > 0 KL.......
Bài 8. Cho đa thức Q(x) = 5x3 - x2 +1 - x3 + 2x4 - 4x3 - x4 + 3x2. a) Thu gọn và sắp xếp các hạng tử của đa thức (Q(x) theo luỹ thừa giảm của biến.b) Tính Q(2) ; Q(-2).c) Chứng tỏ rằng đa thức trên không có nghiệm.
BÀI
NỘI DUNG
a) Q(x) = x4 + 2x2 +1	
b) Q(2) = 24 + 2.22 + 1 = 25	
 Q(-2) = (-2)4 + 2(-2)2 +1= 25	
c) Ta có: x4 0 x	
	 2x20 x	
Þ Q(x) = x4 + 2x2+1 0 + 0 +1 >0 x	
Þ Đa thức trên không có nghiệm