Bài tập ôn thi đại học môn Toán - Chương IV: Hình trụ-Hình nón-Hình cầu - Nguyễn Duy Hoàn

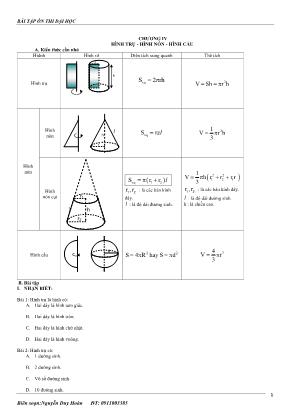
BÀI TẬP ÔN THI ĐẠI HỌC 
Biên soạn:Nguyễn Duy Hoàn ĐT: 0911003385 
1 
 CHƯƠNG IV 
HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU 
A. Kiến thức cần nhớ 
Hidnh Hình vẽ Diện tích xung quanh Thể tích 
Hình trụ 
xqS 2 rh  
2V Sh r h   
Hình 
nón 
Hình 
nón 
xqS r  l 
21V r h
3
  
Hình 
nón cụt 
 xq 1 2S r r   l 
1 2r ,r : là các bán kính 
đáy. 
l : là độ dài đường sinh. 
 2 21 2 1
1
V h r r r r
3
    
1 2r ,r : là các bán kính đáy. 
l : là độ dài đường sinh. 
h : là chiều cao. 
Hình cầu 
2 2S 4 R hay S d    
34V r
3
  
 B. Bài tập 
I. NHẬN BIẾT: 
Bài 1: Hình trụ là hình có: 
A. Hai đáy là hình tam giác. 
B. Hai đáy là hình tròn. 
C. Hai đáy là hình chữ nhật. 
D. Hai đáy là hình vuông. 
Bài 2: Hình trụ có: 
A. 1 đường sinh. 
B. 2 đường sinh. 
C. Vô số đường sinh. 
D. 10 đường sinh. 
r 
h 
o 
r1 
o 
r2 
l h 
 
R  
h 
l
r 
BÀI TẬP ÔN THI ĐẠI HỌC 
Biên soạn:Nguyễn Duy Hoàn ĐT: 0911003385 
2 
Bài 3: Khi cắt hình trụ bởi một mặt phẳng song song với trục của nó ta được mặt phẳng cắt là hình: 
A. Một hình chữ nhật. 
B. Một hình tròn. 
C. Một hình tam giác. 
D. 10 hình tam giác. 
Bài 4: Khi cắt hình trụ bởi một mặt phẳng song song với đáy thì phần mặt cắt là hình: 
A. Hình chữ nhật. 
B. Hình tròn. 
C. Hình Vuông. 
D. Tam giác 
Bài 5: Khi quay một tam giác vuông một vòng quanh một cạnh góc vuông cố định thì hình tạo thành là một 
A. Hình trụ B. Hình nón 
 C. Hình hộp chữ nhật D. Hình cầu 
Bài 6:: Nếu cắt hình nón bởi một mặt phẳng song song với đáy thì mặt cắt là một 
A. Hình tròn B. Hình chữ nhật 
C Hình tam giác D. Hình thang cân 
Bài 7: Công thức tính diện tích xung quanh của hình nón là: 
 B. 
C. D. 
Bài 8: Khi cắt hình cầu bán kính R bởi một mặt phẳng. Ta được mặt cắt là: 
A. Là một hình tròn 
B. Là một đường tròn 
C. Là một hình vuông 
Bài 9: Khi cắt mặt cầu có bán kính R bởi một mặt phẳng. Ta được: 
A. Hình chữ nhật 
B. Đường tròn 
C. Hình tròn 
Bài 10: Mặt cầu có diện tích là 25 cm2. Khi đó đường kính của mặt cầu là: 
A. cm B. cm C. cm D. cm 
Bài 11: : Công thức tính thể tích của hình nón là: 
 A. B. 
 C. D. 
II. THÔNG HIỂU: 
 Bài 1. Quan sát hình dưới đây và cho biết chiều cao của hình trụ. 
A. 10cm 
B. 8cm 
C. 5 cm 
D. 4cm 
BÀI TẬP ÔN THI ĐẠI HỌC 
Biên soạn:Nguyễn Duy Hoàn ĐT: 0911003385 
3 
Bài 2. Quan sát hình dưới đây và cho biết bán kính đáy của h?nh trụ. 
A. 10cm 
B. 8cm 
C. 4cm 
D. 5 cm 
Bài 3. Quan sát hình dưới đây và cho biết bán kính đáy của h?nh trụ. 
A. 11cm 
B. 1 cm 
C. 0.5 cm 
D. 5.5 cm 
Bài 4. Diện tích xung quanh của một hình trụ có chu vi hình tròn đáy là 13cm và chiều cao 3cm là: 
A. 16 cm2 
B. 10 cm2 
C. 39 cm2 
 Bài 5. Bán kính đáy của hình nón bằng 4cm, độ dài đường sinh bằng 8cm thì diện tích xung quanh của hình nón bằng: 
A. 31 B. 32 C. 33 D. 34 
 Bài 6. Bán kính đáy của hình nón bằng 3cm, độ dài đường cao bằng 7cm thì thể tích của h?nh nón bằng: 
A. 21 B. 22 C. 23 D. 24 
 Bài 7. Bán kính đáy của hình nón bằng 6cm, độ dài đường cao bằng 8cm thì độ dài đường sinh của hình nón bằng: 
A. 8 cm B. 9 cm C. 10 cm D. 11cm 
Bài 8. Bán kính đáy của hình nón bằng 2cm, độ dài đường sinh bằng 5cm thì diện tích toàn phần của hình nón bằng: 
A. B. C. D. 
Bài 9. Bán kính hai đáy của hình nón cụt bằng 2cm và 5cm, độ dài đường sinh bằng 7cm thì diện tích xung quanh của hình nón 
cụt bằng: 
A. B.49 C. 50 D. 51 
Bài 10. Diện tích của mặt cầu có bán kính R = 3cm là: 
A. 113,04cm2 B. 36,68cm2 C. 35,68cm2 
Bài 11. Diện tích của mặt cầu là: 64cm2. Khi đó bán kính của mặt cầu là: 
A. R= cm B.R = cm C. R = cm D. R = 
Bài 12. Thể tích của mặt cầu có bán kính R = 3cm là: 
A. V = 113,02cm3 B. V = 113,03cm3 
C, V = 113,04cm3 D. V = 113,05cm3 
BÀI TẬP ÔN THI ĐẠI HỌC 
Biên soạn:Nguyễn Duy Hoàn ĐT: 0911003385 
4 
Bài 13. Tính bán kính của một hình cầu có thể tích V = 3052,08cm3 
A.R = 9cm B. R = 10cm C. R = 11cm D. R = 12cm 
Bài 14. Một hình cầu có diện tích hình tròn lớn là 50,24cm2. Tính diện tích mặt cầu( làm tr?n đến chữ số thập phân thứ 2) 
III. VẬN DỤNG: 
 Bài 1. Một hình trụ có bán kính đáy 5cm và chiều cao của hình trụ là 10cm. 
Lấy π = 3,14 Hãy tính: 
a. Diện tích toàn phần của hình trụ? 
b. Tính thể tích của hình trụ? 
Bài 2. Một bóng đèn huỳnh quang dài 1,2m. đường kính của đường tròn đáy là 4cm, được đặt khít vào một ống giấy cứng dạng 
hình hộp(h82). 
a. Tính diện tích phần cứng dùng để làm hộp.(Hộp mở hai đầu, không tính lề và mép dán). 
b. Tính thể tích của bóng đèn? 
Bài 3. Hình trụ có đường kính đường tròn đáy là 10 mm và chiều cao bằng 4/5 đường 
kính. Lấy π = 3,14 Hãy tính: 
a. Thể tích của hình trụ. 
b. Diện tích xung quanh của h?nh trụ. 
Bài 4. Cho hình chữ nhật ABCD (AB = 2a, BC = a). Quay hình chữ nhật đó quanh AB th? được hình trụ có thể tích V1; quay 
quanh BC thì được hình trụ có thể tích V2. 
a. Tính V1, V2 theo a? 
b. Chứng minh rằng: V2 = 2V1 
Bài 5. Đường ống nối hai bể cá trong một thủy cung ở miền nam nước Pháp có dạng hình trụ, độ dài của đường ống là 30m ( 
h86). Dung tích của đường ống nói trên là 1 800 000 lít. 
a. Tính diện tích đáy của đường ống. 
b. Tính bán kính đáy của đường ống. 
Bài 6. Bán kính hình nón bằng 3m, chiều cao bằng 4m. Lấy π = 3,14 h?y tính 
a) Tính độ dài đường sinh. 
b) Tính diện tích xung quanh và thể tích hình nón. 
Bài 7. Một hình nón tạo ra khi quay một vòng quanh cạnh AB của tam giác vuông 
 cân ABC (vuông ở A) AB = AC = 5cm. 
a) Tính diện tích xung quanh và diện tích toàn phần của h?nh nón. 
b) Tính thể tích hình nón. 
Bài 8. Cho một hình nón có diện tích xung quanh , độ dài đường sinh 
 bằng 10cm. 
a) Tính diện tích toàn phần. 
b) Tính thể tích hình nón. 
Bài 9. Người ta cần làm một cái lều h?nh nón cao 3m, bán kính đường tr?n đáy 2m. 
 Biết rằng diện tích vải thừa ra để làm mép khâu bằng 5% diện tích xung quanh. 
a) Tính độ dài đường sinh. 
b) Tính số vải cần dùng để lợp chiếc lều đó. 
 Bài 10. Cho hình nón cụt với hai bán kính đáy lần lượt bằng 6cm và 10cm, đường sinh bằng 16cm. 
a) Tính diện tích xung quanh. 
b) Tính đường cao và thể tích h?nh nón cụt. 
BÀI TẬP ÔN THI ĐẠI HỌC 
Biên soạn:Nguyễn Duy Hoàn ĐT: 0911003385 
5 
Bài 11. Tính diện tích mặt cầu biết bán kính là R = 8 cm 
Bài 12. Một hình cầu có thể tích là V = 523,33 cm2. 
Tính bán kính của hình tròn lớn. 
 ( làm tròn đến chữ số thập phân thứ 2) 
Bài 13. Một hình cầu có diện tích hình tròn lớn là 208,4cm3. 
Tính thể tích của hình cầu.( Làm tròn đến chữ số thập phân thứ 2) 
Bài 14. Một bể cá (như hình vẽ) gồm một hình trụ ngoại tiếp 
hình cầu: 
Tính thể tích không khí c?n lại mà thể tích hình trụ chưa 
chiếm chỗ hết. 
Biết đường sinh của h?nh trụ là 20cm, đường kính của 
 hình cầu là 20cm 
( kết quả Làm tròn đến chữ số thập phân thứ 2) 
Bài 15. Cho một hình cầu có bán kính là 27cm. 
Tính diện tích hình tròn lớn, 
diện tích mặt cầu,thể tích hình cầu. 
IV. VẬN DỤNG CAO: 
Bài 1. Chiều cao của một hình trụ bằng bán kính đường tròn đáy. 
Diện tích xung quanh của hình trụ là 314 (cm2). 
Hãy tính bán kính đường tròn đáy và thể tích hình trụ 
(làm tròn kết quả đến số thập phân thứ hai). 
Bài 2. Một hình trụ có bán kính đáy là 7 cm, diện tích xung quanh bằng 352 cm2. 
Tính chiều cao của hình trụ: 
Bài 3. Chiều cao của hình trụ bằng 7cm, bán kính đáy bằng 5cm. Tính diện tích của thiết diện song song với trục và cách trục 
4cm ( Khoảng cách từ trục đến thiết diện chính là khoảng cách từ tâm đường tròn đáy đến dây cung mà mặt phẳng cắt hình tròn 
đáy của hình trụ 
Bài 4. Cho tam giác ABC vuông ở A. Gọi theo thứ tự là thể tích của những hình sinh ra khi quay tam giác ABC một 
vòng quanh các cạnh BC, AB, AC. Chứng minh rằng: 
Bài 5. Người ta sơn 100 chậu đựng nước dạng hình nón cụt, bán kính miệng chậu là 30 cm, bán kính đáy 
chậu là 25cm, đường sinh27,5cm. Biết rằng cứ sơn 1 thì hết 150 gam dầu sơn. Hỏi sơn cả hai mặt chậu 
thì hết bao nhiêu kg dầu sơn? 
Bài 6. Thiết diện qua trục của một hình nón là tam giác đều cạnh a. 
Tính diện tích toàn phần và thể tích của h 
20cm 
20cm 
BÀI TẬP ÔN THI ĐẠI HỌC 
Biên soạn:Nguyễn Duy Hoàn ĐT: 0911003385 
6 
Bài 7. Một hình cầu nội tiếp hình nón. Khi h?nh cầu tiếp xúc với tất cả các đường sinh và mặt đáy của hình nón. Tính diện tích 
mặt cầu và thể tích hình cầu nội tiếp hình nón mà thiết diện qua trục hình nón là tam giác đều cạnh a. 
Bài 7. Một hình nón có đỉnh là tâm của một hình cầu có đáy là một hình tròn có bán kính là 40dm tạo bởi mặt phẳng cắt hình cầu 
và cách tâm hình cầu là 9dm. tính thể tích hình cầu. 
Bài 8. Một hình cầu có V = = ᴨ4 một hình cầu khác có bán kính bằng bán kính của hình cầu thứ nhất. Tính thể tích của hình 
cầu thứ 2. 
O 
a 
H 
A B 
a 
S 
a 
O 
A H