Bài hình kiểm tra học sinh giỏi Toán 8 hay và rất khó - Nguyễn Khánh Ninh

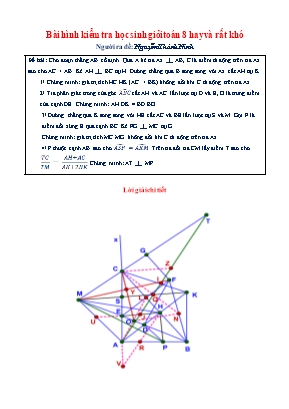
Bài hình kiểm tra học sinh giỏi toán 8 hay và rất khó
Người ra đề: Nguyễn Khánh Ninh 
Đề bài: Cho đoạn thẳng AB cố định. Qua A kẻ tia Ax _|_ AB, C là điểm di động trên tia Ax sao cho AC > AB. Kẻ AH _|_ BC tại H. Đường thẳng qua B song song với Ax cắt AH tại K
 1/ Chứng minh: giá trị tích HC.HK.(AC + BK) không đổi khi C di động trên tia Ax
 2/ Tia phân giác trong của góc cắt AH và AC lần lượt tại D và E, O là trung điểm 
 của cạnh DE. Chứng minh: AH.DK = BD.BO
 3/ Đường thẳng qua K song song với HE cắt AC và BE lần lượt tại S và M. Gọi F là 
 điểm đối xứng E qua cạnh BC. Kẻ FG _|_ MC tại G. 
 Chứng minh: giá trị tích MC.MG không đổi khi C di động trên tia Ax 
 4/ P thuộc cạnh AB sao cho . Trên tia đối tia CM lấy điểm T sao cho 
 . Chứng minh: AT _|_ MP 
Lời giải chi tiết
1/ Tích HC.HK.(AC + BK) không đổi
AB _|_ Ax và BK // Ax => AB _|_ BK
Xét CHA và CAB:
 là góc chung ; 
=> CHA ~ CAB (g – g) => => AC2 = HC.BC (1a)
Xét KHB và KBA:
 là góc chung ; 
=> KHB ~ KBA (g – g) => => KB2 = HK.AK (1b)
Xét ABC và BKA:
 ; (cùng phụ với )
=> ABC ~ BKA (g – g) => => AB2 = AC.BK (1c)
Lại có: Tứ giác ABKC là hình thang vuông (AC và BK cùng vuông góc với AB). Kí hiệu S là diện tích thì: AK.BC = 2SABKC (do AK _|_ BC)
Mà (AC + BK).AB = 2SABKC (Tứ giác ABKC là hình thang vuông tại B và K)
=> (AC + BK).AB = AK.BC (1d)
Từ (1a), (1b), (1c), (1d) => AB4 = AC2.BK2 = HC.BC.HK.AK = HC.HK.AB.(AC + BK)
=> HC.HK.(AC + BK) = AB3 (không đổi) (đpcm) 
2/ AH.DK = BD.BO
Ta có: (góc ngoài tam giác BDK)
Mà (cùng phụ với ) và (gt)
Nên: 
=> Tam giác KBD cân tại A => DK = BK (2a) 
Ta có: (2 góc ở vị trí đối đỉnh)
Mà (cmt) và (2 góc ở vị trí sole trong do AC // BK)
=> => Tam giác ADE cân tại A.
Lại có AO là đường trung tuyến của tam giác ADE (OD = OE) => AO _|_ BE
Xét AHB và ABK:
 là góc chung ; 
=> AHB ~ ABK (g – g) => => AH.BK = AB.BH (2b)
Xét HBD và OBA:
 ; (gt)
=> HBD ~ OBA (g – g) => => AB.BH = BD.BO (2c)
Từ (2a), (2b), (2c) => AH.DK = AH.BK = AB.BH = BD.BO 
=> AH.DK = BD.BO (đpcm) 
3/ Tích MC.MG không đổi
HE // MK (gt) nên (định lí talet trong tam giác DMK) (3a)
BD là phân giác góc nên: (tính chất phân giác trong tam giác AHB)
Xét BHA và BAC:
 là góc chung ; 
=> BHA ~ BAC (g – g) => => AB2 = BH.BC
Từ đó suy ra => 
Do AC // BK và từ các hệ thức trên ta có: 
Lại có: AC2 = BC2 – AB2 = (BC – AB).(BC + AB). (định lí pitago trong tam giác ABC) 
=> 
=> (3b) 
Xét HBD và ABE:
 ; (gt)
=> HBD ~ ABE (g – g) => . Mà (cmt)
=> => (3c)
Từ (3a), (3b), (3c) => MD = BE 
Ta có: (cùng phụ với ). Mà (gt) => 
Xét HBD và OAE:
 ; (cmt)
=> HBD ~ OAE (g – g) => . (3d)
BE là phân giác góc nên: (tính chất phân giác trong tam giác ABC)
Từ các chứng minh trên ta có:
 => (3e)
Từ (3d), (3e) nhân vế theo vế => 
Xét HBM và OAC:
 (cmt) ; (cmt)
=> HBM ~ OAC (c – g – c) (3f)
Xét BOA và BAE:
 ; là góc chung
=> BOA ~ BAE (g – g) => => AB2 = BO.BE
Mà AB2 = BH.BC (cmt) => BH.AB = BO.BE
Gọi N là trung điểm của cạnh BF, EF cắt BC tại L. Do E đối xứng F qua cạnh BC
=> BE = BF = 2BN ; ; LE = LF ; EF _|_ BC
Ta có: MD = BE => ME = MD – DE = BE – DE = BD
=> OM = OE + ME = OD + BD = BO => BM = 2BO
Do đó: BN.BM = 2BO. = BO.BE => BH.BC = BN.BM => 
Xét HBM và NBC:
 (cmt) ; (cmt)
=> HBM ~ NBC (c – g – c) (3g)
Từ (3f), (3g) => OAC ~ NBC => 
Và => (cùng cộng thêm )
Xét ACB và OCN:
 (cmt) ; (cmt)
=> ACB ~ OCN (c – g – c) => => OC _|_ ON
Ta có: NB = NF và OB = OM (cmt) => ON là đường trung bình của tam giác MBF
=> MF // ON, mà OC _|_ ON (cmt) => OC _|_ MF
Ta có: OM = OB (cmt) và OA _|_ BM => Tam giác ABM cân tại M 
=> . mà (gt) => 
=> AM // BC (2 góc ở vị trí sole trong). Mà AH _|_ BC => AM _|_ AH
Theo như trên ta có: AB2 = BO.BE = OM.MD
Xét ABE vuông tại A và LBE vuông tại L:
BE là cạnh chung ; 
=> ABE = LBE (ch – cgn) => AB = BL => Tam giác ABL cân tại B 
Có BE là đường phân giác tam giác cân ABE => AL _|_ BE
Mà OA _|_ BE (cmt) => 3 điểm A, O, L thẳng hàng hay OL _|_ BE
Ta có: OE = OD và LE = LF => OL là đường trung bình của tam giác EDF
=> DF // OL. Mà OL _|_ BE (cmt) => DF _|_ BE.
Cho MF cắt OC tại Y.
Xét MYO và MDF:
 ; là góc chung
=> MYO ~ MDF (g – g) => => MO.MD = MY.MF
Xét MYC và MGF:
 ; là góc chung
=> MYC ~ MGF (g – g) => => MY.MF = MC.MG
Từ các kết quả trên cho: MC.MG = MY.MF = MO.MD = AB2
=> MC.MG = AB2 (không đổi) (đpcm)
4/ AT _|_ MP
Cho AT cắt các cạnh KC, MK và HE lần lượt tại I, Q và J. Cho HE cắt AM tại U
Áp dụng định lí Menelaus trong tam giác CMK: 
 = 1 => (4a)
HE// MK nên áp dụng hệ quả talet trong các tam giác AQM và AQM:
 => (4b)
Z thuộc cạnh AT sao cho CZ // MK // HE, áp dụng hệ quả talet trong các tam giác AQK và ACZ: (4c)
Từ (4a), (4b), (4c) => (4d)
CHA ~ CAB (cmt) => => AH.AC = HC.AB
ABC ~ BKA (cmt) => => AB.BC = AC.AK
Theo như trên đã có: AC2 = HC.BC và AC.BK = AB2. Biến đổi:
 => (4e)
AC // BK nên định lí talet: (4f)
Theo như trên đã có: => (4g)
AM // BC nên: (định lí ta let) (4h)
Thế (4e), (4f), (4g), (4h) vào (4d) => 
=> => => HE = 2JE => JE = JH
Ta có: BO.BE = BH.AB (cmt) => 
Xét BDO và BEH:
 (cmt) ; là góc chung
=> BDO ~ BEH (c – g – c) => 
=> (kề bù với 2 góc bằng nhau). Mà (OAC ~ HBM) 
=> 
=> (= )
Xét AKM và ASP:
 ; (gt)
=> AKM ~ ASP (g – g) => 
Xét AHB và ABK:
 ; là góc chung
=> AHB ~ ABK (g – g) => 
Mà đã có: AM = AB (cmt) => . 
Từ đó suy ra => 
Ta có: (2 góc ở vị trí sole trong do MK // HE)
 (2 góc ở vị trí sole trong do AM // BC)
Xét ASM và CEH:
 (cmt); (cmt)
=> ASM ~ CEH (g – g) => .Suy ra 
Xét CHE và AHP:
 (cmt) ; (cùng phụ với )
=> CHE ~ AHP (c – g – c) => 
Mà (cmt) => 
Theo trên đã có: . Mà (cmt) 
=> => => 
Mà (cmt) => 
=> DP // BC (định lí talet đảo trong tam giác AHB), mà AH _|_ BC => DP _|_ AH
Gọi V là điểm đối xứng E qua A, HV cắt AC tại R thì AV = AE = AD
DP // BC nên theo hệ quả talet tam giác AHB: 
=> => 
Xét DPH và APV:
 (cmt) ; 
=> DPH ~ APV (c – g – c) => 
Mà (cmt) => 
Xét AVP và AHM:
 ; (cmt)
=> AVP ~ AHM (g – g) => 
Ta có: 
Xét AVH và APM:
 (cmt) ; (cmt)
=> AVH ~ APM (c – g – c) => 
Ta có: (2 góc ở vị trí đối đỉnh) và (tam giác ARV vuông tại A) => => MP _|_ HV
Ta có: JE = JH (cmt) và AE = AV => AJ là đường trung bình tam giác HEV 
=> AJ // HV hay AT // HV.
Mà MP _|_ HV (cmt) => AT _|_ MP (đpcm)