Ôn tập môn Hình học lớp 10 - Bài toán về hàng điểm điều hòa

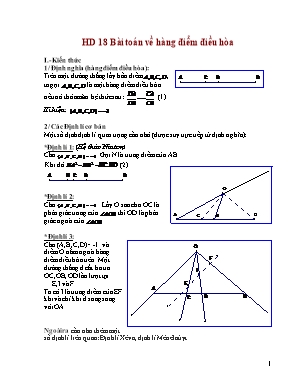
HD 18 Bài toán về hàng điểm điều hòa
I.- Kiến thức
1/ Định nghĩa (hàng điểm điều hòa):
Trên một đường thẳng lấy bốn điểm, ta gọi là một hàng điểm điều hòa nếu nó thỏa mãn hệ thức sau: (1) 
Kí hiệu: 
2/ Các Định lí cơ bản
Một số định định lí quan trọng cần nhớ (được suy trực tiếp từ định nghĩa):
*Định lí 1: (Hệ thức Niutơn)
Cho . Gọi N là trung điểm của AB.
 Khi đó (2)
*Định lí 2:
Cho . Lấy O sao cho OC là phân giác trong của thì OD là phân giác ngoài của .
*Định lí 3:
Cho (A,B,C,D) = -1 và điểm O nằm ngoài hàng điểm điều hòa trên. Một đường thẳng d cắt ba tia OC,OB, OD lần lượt tại 
 E,I và F. 
Ta có I là trung điểm của EF khi và chỉ khi d song song với OA.
Ngoài ra cần nhơ thêm một số dịnh lí liên quan: Định lí Xêva, định lí Mênêlaúyt
II. Các bài toán về hàng điểm điều hòa
Bài toán 1:
Cho tam giác ABC. Lấy E trên BC, F trên AC và K trên AB sao cho AE,BF,CK đồng quy tại một điểm. Khi đó nếu T là giao điểm của FK với BC thì 
Giải: 
Trong tam giác ABC:
+Áp dụng định lí Xêva với ba đường đồng quy AE,BF,CK ta có:
 (1)
+Mặt khác áp định lí Mênêlaúyt với ba điểm thẳng hàng T,K,F lại cho ta:
 (2)
Nhân (1) và (2) vế theo vế suy ra: 
Theo định nghĩa thì ,đây chính là đpcm.
Bài toán 2:
Cho tam giác ABC và H là chân đường cao kẻ từ A. Trên đoạn thẳng AH ta lấy một điểm I bất kì rồi kẻ BI cắt AC tại E và CI cắt AB tại F.Chứng minh rằng AH là phân giác của 
Giải: 
a/ Cách 1 dưới đây là lời giải rất độc đáo của anh Hatucdao
 “Kết quả là hiển nhiên khi tam giác ABC cân. Giả sử ABC không cân ta có thể giả sử AC>AB.Dựng tam giác ABP cân tại A và AP cắt HE tại Q. Gọi F’ là điểm đối xứng của Q qua AH. 
 Khi đó AH là phân giác của và 
Áp dụng định lí Mênêlaúyt cho tam giác ACP với ba điểm thẳng hàng H,Q,E ta có:
Theo định lí Ceva ta có đồng quy từ đó suy ra đpcm”
Một viên ngọc không dấu vết nhưng phải công nhận là rất khó nghĩ ra. 
Dẫu sao đi nữa thì việc cảm nhận vẻ đẹp tinh túy của lời giải trên cũng giúp chúng ta thấm thía và quý trọng hơn đối với cách làm dưới đây, bởi điều quan trọng hơn một lời giải, là nó cho ta thấy được gốc rễ của vấn đề:
Cách 2: Kẻ EF cắt BC tại K theo bài toán 1 ta có (1)
Gọi L là giao điểm của EF với AH.
Từ (1) suy ra suy ra (định lí chùm điều hòa)
Vì nên theo nhận xét trong định lí 2 ta có đpcm.
*Nhận xét: Quá ngắn gọn phải không, tôi nghĩ rất có thể bài toán trên đã được đặt ra như vậy. Các bạn có thể thấy chỉ vài biến đổi nhỏ và một kĩ xảo để che dấu điểm K đã khiến cho bài toán 2 trở nên cực khó. Tất nhiên từ lời giải này chúng ta có thể phát biểu bài toán tổng quát hơn như bài toán 3:
Bài toán 3:(đề thi Iran)
Cho tam giác ABC, lấy T,E,F lần lượt thuộc các đoạn BC,CA,AB sao cho 3 đường thẳng AT,BE,CF đồng quy tại một điểm.Gọi L là giao điểm của AT và EF.Gọi H là hình chiếu của L xuống BC. Chứng minh rằng LH là phân giác của .
*Nhận xét:
Nói chung từ 1 hàng điểm điều hòa ban đầu ta có thể “sinh sôi nảy nở” ra rất nhiều hàng điểm điều hòa khác mà một trong chúng nếu kết hợp với các định lí 2 và 3 sẽ cho ta rất nhiều tính chất thú vị. Thí dụ các bài 2 và 3 là “sản phẩm” của định lí 2. 
Bài toán 4: (dụng định lí 3)
Cho tam giác ABC, lấy T,E,F lần lượt thuộc các đoạn BC,CA,AB sao cho 3 đường thẳng AT,BE,CF đồng quy tại điểm I. Kẻ đường thẳng qua I song song với TE và cắt TF,TB lần lượt tại M và L. Chứng minh rằng M là trung điểm của LI.
Qua các Bài toán 1,2 3,4 thí dụ trên các bạn có thể thấy từ một vấn đề người ta có thể phát biểu dưới những cách khác nhau, những cách mà khi đọc đề chúng ta không hề thấy bất kì một liên hệ gì từ chúng, nhưng thực ra tất cả chúng đều xuất phát từ một gốc rễ. Nắm được gốc rễ tức là ta đã nắm được bài toán vậy.
Tất nhiên từ bài toán 1 sẽ sản sinh ra cả một lớp các bài toán rộng lớn, tôi không có thời gian nêu thêm ra đây mà chỉ hi vọng các bạn nếu gặp một trong số đó sẽ nhanh chóng cho nó “lộ rõ nguyên hình”.
Bây giờ xin đi vào một không gian mới hơi khác một chút với các cách khai thác đã nêu ở trên nhằm giúp các bạn có một cái nhìn sâu sắc hơn cho bài toán 1. Nhưng trước hết tôi sẽ trang bị cho các bạn một số tính chất cần thiết, rồi sau đó chúng ta sẽ tìm cách liên hệ với bài toán 1 sau.
Bài toán 5 (Tính chất 1):
Cho tam giác ABCD ngoại tiếp đường tròn tâm (O). M,N,P,Q lần lượt là các tiếp điểm của AB,BC,CD,DA với đường tròn; khi đó ta có MP,NQ,AC,BD đồng quy tại một điểm.
Giải:
Hạ 
Chú ý 
Do đó nếu gọi I là giao điểm của AC với MP thì ta có: (1)
Tương tự gọi là giao điểm của AC với NQ thì ta cũng có: (2)
Chú ý AM=AQ và PC=NC nên từ (1) và (2) suy ra 
suy ra MP,NQ,AC đồng quy (3) 
Lập luận tương tự ta có 
 MP,NQ,BD đồng quy (4)
Kết hợp (3) và (4) ta được đpcm.
Bài toán 6 (Tính chất 2): 
Cho hai điểm A,B cố định . M là điểm thỏa mãn (k là hằng số), khi đó quỹ tích điểm M là một đường tròn cố định.
Gợi ý: 
Lấy N à K trên AB sao cho MN,MK lần lượt là phân giac trong và phân giác ngoài của . Hãy chứng tỏ N,K cố định và quỹ tích điểm M là đường tròn đường kính NK.
Việc chứng minh này không khó nên xin nhường cho bạn đọc.
*Chú ý tính chất hai là một bài toán nổi tiếng và quỹ tích điểm M được gọi là “đường tòn Apôlôut” 
Bài toan 7 (Tính Chất 3):
Cho đường tròn (O). Lấy một điểm A ngoài đường tròn (O), từ A ta kẻ hai tiếp tuyến AK,AN và một cát tuyến ACD bất kì đối với đường tròn trên. Hai tiếp tuyến qua C và D đối với đường tròn cắt nhau tại M. Khi đó ta có K,M,N thẳng hàng.
Giải:
Dễ dàng chứng minh (1)
Gọi N’ là giao điểm của MK với (O) ta chứng minh được (2) 
Gọi E và F lần lượt là phân giác trong và phân giác ngoài của 
Sử dụng tính chất 2 cho (1) và (2) suy ra N và N’ đều thuộc đường tròn đường kính EF. 
Mặt khác N và N’ đều thuộc (O) do đó N và N’ là giao điểm giữa (O) với đường tròn đường kính EF.Bây giờ ta chú ý đường tròn(O) và đường tròn đường kính EF cắt nhau tại hai điểm nằm trên hai mặt phẳng khác nhau bờ DC trong khi N,N’ lại cùng trên một mặt phẳng bờ DC những điều trên cho tađpcm
Bài toán 8 (Tính chất 4):
Cho tứ giác ABCD ngoại tiếp đường tròn tâm (O). M,N,P,Q lần lượt là các tiếp điểm của AB,BC,CD,DA với đường tròn. Chứng minh rằng MQ,NP và DB đồng quy tại một điểm.
Giải:
Gọi K là giao điểm của QM với DB 
Áp dụng định lí Mênêlaúyt cho tam giác ABD với ba điểm thẳng hàng Q,M,K ta có:
 (1)
Chú ý và 
Do đó từ (1) suy ra 
Theo định lí Mênêlaúyt đảo suy ra K,N,P thẳng hàng suy ra đpcm
Bài 9 (Tính chất 5): 
Cho tứ giác ABCD ngoại tiếp đường tròn tâm (O). M,N,P,Q lần lượt là các tiếp điểm của AB,BC,CD,DA với đường tròn. Gọi K là giao điểm của MQ với NP.Chứng minh rằng .
Giải:
Gọi E và F là hai giao điểm của AC với (O). 
Hai tiếp tuyến qua E và F đối với (O) cắt nhau tại K’
Theo tính chất 3 suy ra K’,N,P thẳng hàng và K’,M,Q thẳng hàng hay K’ là giao điểm của MQ với NP hay . 
Vậy KE,KF là hai tiếp tuyến của K với (O) suy ra hay (đpcm)
Bài toán 10 (Tính chất 6):
Cho tam giác ABCD ngoại tiếp đường tròn tâm (O). M,N,P,Q lần lượt là các tiếp điểm của AB,BC,CD,DA với đường tròn. Gọi K là giao điểm của MQ với NP và I là giao điểm của MP với QN. Chứng minh rằng .
Giải:
*Áp dụng định lí Mênêlaúyt cho tam giác ABD với 3 điểm thẳng hàng K,M,Q ta có:
 hay (vì QA=MA) (1)
*Mặt khác theo lời giải trong tính chất 1 thì ta đã biết: (2)
Từ (1) và (2) suy ra 
Vì I nằm trong đoạn BD và K nằm ngoài đoạn BD nên: 
Vậy (đpcm)
*Nhận xét: Việc xuất hiện hàng điểm điều hòa (tính chất 6) ở đây đóng một vai trò vô cùng quan trọng, để dễ hiểu các bạn hãy tưởng tượng năm tính chất 1,2,3,4,5 như một kho thuốc súng có sức tàn phá khủng khiếp nhưng đang bị đè nén trong bao, và tính chất 6 chính là mồi kích hoạt kho thuốc súng ấy để tạo nên một sự bùng nổ vô cùng ghê gớm, đến mức, hàng loạt các tính chất mới được sinh ra dồn dập đến chóng mặt
III.- Một số bài trên “tạp chí Toán học và tuổi trẻ”:
Bài toán 11:
Cho tứ giác ABCD ngoại tiếp đường tròn (O) . Gọi E,F lần lượt là giao điểm AC với (O). Hạ . Chứng minh rằng (*)
Lời giải:
Gọi M,N,P,Q lần lượt là tiếp điểm của AB,BC,CD,DA với (O). Đặt , và . Vì hai tứ giác KEOH và KFOH nội tiếp suy ra 5 điểm K,E,O,H,F cùng thuộc một đường tròn suy ra do vậy để chứng minh (*) ta cần chứng minh HI là phân giác .
Thật vậy theo tính chất 5 suy ra HI vuông góc AL và theo kết quả tính chất 6 thì ta đã có 
 do vậy áp dụng định lí 2 suy ra HI là phân giác (đpcm)
Bài toán 12:
Cho tứ giác ABCD ngoại tiếp đường tròn (O) và M,N,P,Q lần lượt là các tiếp điểm của AB,BC,CD,DA. Đặt ,,,. Chứng minh rằng 4 điểm K,L,E,F cùng nằm trên một đường thẳng.
Lời giải:
Gọi I là giao điểm giữa BD với AC, E’ là giao điểm DB với KL, T là giao điểm CE’ với DK, theo bài toán 1 thì suy ra theo định lí chùm điều hòa suy ra tuy nhiên theo tính chất 6 thì đã có 
Do vậy suy ra E,K,L thẳng hàng (1) . 
Lập luận tương tự cũng có F,K,L thẳng hàng (2). 
Kết hợp (1) và (2) suy ra đpcm
Bài toán 13:
Cho tứ giác MNPQ nội tiếp đường tròn (O) có , , .Chứng minh rằng I là trực tâm của tam giác KOL
Lời giải:
Kẻ 4 tiếp tuyến qua M,N,P,Q chúng cắt nhau tại 4 điểm là A,B,C,D (hình vẽ) 
Theo tính chất 1 thì I cũng là giao điểm của AC với BD
Theo tính chất 5 thì 
Theo tính chất 4 thì D,B,K thẳng hàng
Suy ra 
Tương tự 
Vậy ta có đpcm
:
Bài toán 14:
Cho tứ giác ABCD ngoại tiếp đường tròn (O). Đặt , , . OI cắt KL tại H .Chứng minh rằng OH là phân giác của 
Lời giải:
Theo bài 15 thì I là trực tâm của tam giác suy ra 
Đến đây bài toán này đã trở thành bài toán 1.2 và vấn đề được giải quyết.
 Cuối cùng xin nêu lên một vấn đề có tính gợi mở để các bạn xem chơi:
Bài toán 15:
Cho tứ giác ABCD ngoại tiếp đường tròn (O). Đặt , , 
Gọi M,N,P,Q lần lượt là tiếp điểm của AB,BC,CD,DA với (O). Đặt , . Chứng minh rằng 
HD giải:
+Theo bài toán 1.5 thì F,K,E,L thẳng hàng
+Theo tính chất 1.4 thì CA,MN,PQ đồng quy suy ra 
Do vậy theo bài toán 1 ta có 
(Xem hình bên dưới)
Bài toán 16:
Cho A nằm ngoài đường tròn (O), từ A kẻ hai tiếp tuyến AB,AC trong đó B,C là hai tiếp điểm . AO cắt đường trong tại hai điểm E,F và cắt cạnh BC tại K. 
Chứng minh rằng 
HD giải:
Ta có (hệ thức lượng tam giác vuông) (1)
Mặt khác: (2)
Từ (1) và (2) suy ra 
Theo nhận xét của định lí 1 suy ra đpcm
*Một hệ quả thấy ngay từ bài toán này là:
Bài toán 17:
Cho A nằm ngoài đường tròn (O), từ A kẻ hai tiếp tuyến AB,AC trong đó B,C là hai tiếp điểm . Kẻ cát tuyến AMN bất kì trong đó N nằm giữa A và M. AO cắt đoạn BC và cung nhỏ lần lượt tại K và E. Chứng minh rằng ME là phân giác của 
HD giải :
Gọi F là giao điểm thứ hai của AE với (O) theo bài toán 2 ta có 
Vì nên theo nhận xét của định lí 2 ta có đpcm.
Tinh tế hơn một chút ta thu được bài toán rất khó sau:
Bài toán 18:
Cho tam giác ABC bất kì. Lấy một điểm I trong đường tròn sao cho và . Lấy V là một điểm trên AI sao cho . 
Chứng minh rằng BV là phân giác của và CV là phân giác của .
Lời giải:
Gọi E là giao điểm của AI với BC.
Vì (g.g)
Suy ra (1)
Tương tự: (2)
Từ (1) và (2) suy ra E là trung điểm của BC
Vẽ đường tròn đường kính BC đường tròn này đi qua V và nhận E làm tâm do đó
 (3) Từ (1) và (3) suy ra 
Theo nhận xét trong định lí 1 ta có 
Mà Nên theo định lí 2 suy ra BV là phân giác của 
Lập luận tương tự suy ra CV là phân giác của .
Vậy bài toán được giải quyết trọn vẹn.
*Nhận xét:
+Điểm I được xác định như trên có rất nhiều tính chất kì lạ nhưng bài viết đã tương đối dài nên xin tạm gác lại ở đây, nếu có dịp chúng ta sẽ bàn lại vấn đề này sau.
Xuan Binh Than - PHH st theo
Hàng điểm điều hòa - vẻ đẹp quyến rũ trong hình học Kim Luân