Kỳ thi tnpt quốc gia năm 2015 môn : Toán thời gian làm bài: 180 phút (không kể thời gian giao đề)

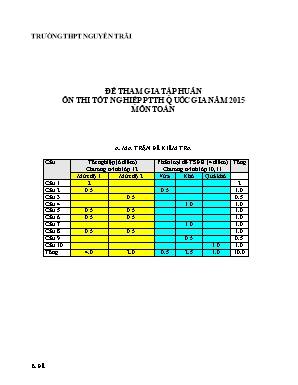
TRƯỜNG THPT NGUYỄN TRÃI
ĐỀ THAM GIA TẬP HUẤN
ÔN THI TỐT NGHIỆP PTTH QUỐC GIA NĂM 2015
MÔN TOÁN
A. MA TRẬN ĐỀ KIỂM TRA 
Câu
Tốt nghiệp (6 điểm)
Chương trình lớp 12
Phân loại để TSĐH (4 điểm)
Chương trình lớp 10,11
Tổng
Mức độ 1
Mức độ 2
Vừa
Khó
Quá khó
Câu 1
2
2
Câu 2 
0.5
0.5
1.0
Câu 3 
0.5
0.5
Câu 4 
1.0
1.0
Câu 5 
0.5
0.5
1.0
Câu 6
0.5
0.5
1.0
Câu 7 
1.0
1.0
Câu 8
0.5
0.5
1.0
Câu 9 
0.5
0.5
Câu 10
1.0
1.0
Tổng
4.0
2.0
0.5
2.5
1.0
10.0
B.ĐỀ
Trường THPT Nguyễn Trãi KỲ THI TNPT QUÔC GIA NĂM 2015
Đề tham gia tập huấn
 MÔN : TOÁN 
 Thời gian làm bài: 180 phút (Không kể thời gian giao đề)
Câu 1.(2.0 điểm).Cho 
Khảo sát sự biến thiên và vẽ đồ thị (C).
Tìm m để phương trình : có 3 nghiệm phân biệt
Câu 2.(1.0 điểm) 
Giải phương trình: 
Tìm các số thực x, y thoả mãn: 
Câu 3 .(0.5 điểm).Giải phương trình: 
Câu 4.(1.0 điểm) Giải bất phương trình: 
Câu 5.(1.0 điểm ) Tính diện tích hình phẳng giới hạn bởi các đường và 
Câu 6.(1.0 điểm) Cho lăng trụ đứng tam giác ABC A'B'C' có đáy ABC là tam giác vuông tại A với AC = a , biết AC’=3a. Tính thể tích lăng trụ và góc hợp bởi BC’ với (AA'C'C)
Câu 7.(1.0 điểm)Trong mpOxy,cho hình vuông ABCD. Gọi M là trung điểm BC, N trên CD sao cho
CN=2ND. Biết và đường thẳng AN có phương trình: . Tìm tọa độ đỉnh A
Câu 8.(1.0 điểm). Trong kg Oxyz, cho A(1; 2; 3) và đường thẳng d : 
1. Lập phương trình mặt cầu (S) có tâm A và đi qua O.
2. Xác định hình chiếu H của A lên (d).
Câu 9.(0.5 điểm).Cho đa giác đều 30 cạnh. Gọi S là tập hợp các tứ giác tạo thành có 4 đỉnh lấy từ các đỉnh của đa giác đều. Chọn ngẫu nhiên một phần tử của S. Tính xác suất để được một hình chữ nhật
Câu 10 .(1.0 điểm). Cho a,b là hai số thực dương thỏa . 
 Tìm giá trị nhỏ nhất của biểu thức 
.......................................................................Hết ...........................................................................
C. Đáp án
Câu 1.1
Đáp án
Thang điểm
Khảo sát sự biến thiên và vẽ đồ thị 
1.0
Tập xác định: 
Sự biến thiên:
y = + ∞; y = - ∞.
0.25
Kết luận: 
+ Hàm số nghịch biến trên (-∞;1), (3:+ ∞), đồng biến trên (1;3)
+ hàm số đạt cực đại tại x = 3; yCĐ = 3, 
 hàm số đạt cực tiểu tại x = 1; yCT = -1
0.25
Bảng biến thiên: 
x
-¥ 1 3 + ¥
y’
 - 0 + 0 -
y
+ 	 3
 -1 -¥
0.25
Điểm đặc biệt: 
Đồ thị: 
0.25
Câu 1.2
Đáp án
Thang điểm
Biện luận theo m số nghiệm của pt: (1)
1.0
0.25
Là phương trình hoành độ giao điểm của (C) và (D):y=2m-1 
 Số nghiệm của(1) là số giao điểm của (C) và (D). 
0.25
Dựa vào đồ thị của (C) và (D), ta có (1) có 3 nghiệm phân biệt khi 
0.25
 và kết luận
0.25
Câu 2.1
Đáp án
Điểm
Giải phương trình: (1)
0.5
Ta có: 
(1) 
0.25
0,25
Câu 2.2
Đáp án
Thang điểm
Tìm các số thực x, y thoả mãn:
0.5
0.25
0.25
Câu 3
 Giải phương trình: (1)
0.5
Điều kiện: 
Khi đó: (1)
0.25
 ( nhận )
Vậy, phương trình có nghiệm 
0.25
Câu 4
Đáp án
Điểm
Giải bất phương trình: 
1.0
ĐK: 
Đặt : , 
0.25
Thay vào (1), ta được: 
0.25
 đúng với 
0.25
0.25
Câu 5
Đáp án
Thang điểm
Tính diện tích hình phẳng giới hạn bởi và 
1.0
Phương trình hoành độ giao điểm của 2 đồ thị:
Û Û 
0.25
Khi đó diện tích hình phẳng là 
= 
0.25
= 
0.25
= = 
0.25
Câu 6
Đáp án
Thang điểm
Cho lăng trụ đứng tam giác ABC A'B'C' có đáy ABC là tam giác vuông tại A với AC = a , = 60 o , biết AC’=3a. 
1.0
Tính thể tích lăng trụ.
 vuông tại A cho
 vuông tại C cho 
0.25
0.25
Tính góc hợp bởi BC’ với (AA'C'C)
AC’ là hình chiếu của BC’ lên (AA’C’C)
 là góc tạo bởi BC’ với (AA'C'C)
0.25
tan= và KL
0.25
Câu 7
Đáp án
Điểm
Trong mpOxy,cho hình vuông ABCD. Gọi M là trung điểm BC, N trên
CD sao cho CN=2ND. Biết và đường thẳng AN có phương 
trình: . Tìm tọa độ đỉnh A
1.0
Đặt AB = a . 
Ta tính được: 
Tính được 
0.25
(AM) qua có dạng 
 . Điều kiện: 
Chọn b=1
0.25
Với 
0.25
Với 
0.25
Câu 8
Trong kg Oxyz, cho A(1; 2; 3) và đường thẳng d : 
1.0
1. Lập phương trình mặt cầu (S) có tâm A và đi qua O.
0.5
0.25
(S) có tâm , bán kính 
Phương trình 
0.25
2. Xác định hình chiếu H của A lên (d).
0.5
(d) có vectọ chỉ phương . qua và vuông góc (d)
Phương trình 
0.25
0.25
Câu 9
Đáp án
Điểm
Cho đa giác đều 30 cạnh. Gọi S là tập hợp các tứ giác tạo thành có 4 đỉnh lấy từ các đỉnh của đa giác đều. Chọn ngẫu nhiên một phần tử của S. Tính xác suất để được một hình chữ nhật
0.5
Số tứ giác tạo thành với 4 đỉnh lấy từ các đỉnh của đa giác đều là . 
Suy ra 
0.25
Gọi A là biến cố được tứ giác là một hình chữ nhật.
Số đường chéo đa giác qua tâm của đa giác đều: 15
Số hình chữ nhật tạo thành : 
0.25
Câu 10
Đáp án
Thang điểm
Cho a,b là hai số thực dương thỏa . Tìm giá trị nhỏ nhất của biểu thức 
1.0
Ta có : 
0.5
Bất đẳng thức Côsi cho :
 Suy ra 
0.25
 đạt khi 
0.25