Kiểm tra Toán 7 - Hình học chương II thời gian: 45 phút

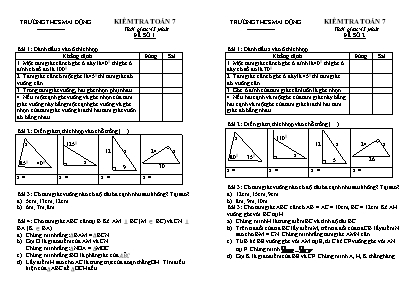
TRƯỜNG THCS MAI ĐỘNG KIỂM TRA TOÁN 7
 -------------- Thời gian: 45 phút
 ĐỀ SỐ 1
Bài 1: Đánh dấu x vào ô thích hợp
Khẳng định
Đúng
Sai
1. Một tam giác cân có góc ở đáy là 400 thì góc ở đỉnh có số đo là 1000
2. Tam giác cân có một góc là 450 thì tam giác đó vuông cân
3. Trong tam giác vuông, hai góc nhọn phụ nhau
4. Nếu một cạnh góc vuông và góc nhọn của tam giác vuông này bằng một cạnh góc vuông và góc nhọn của tam giác vuông kia thì hai tam giác vuôn đó bằng nhau
Bài 2: Điền giá trị thích hợp vào chỗ trống ()
 x
 850 400
 1250
 x
 12 x
 9
 24 x
 30
x = ..
x = 
x = 
x = 
Bài 3: Có tam giác vuông nào có độ dài ba cạnh như sau không? Tại sao?
5cm; 13cm; 12cm 
6m; 7m; 8m
Bài 4: Cho tam giác ABC cân tại B. Kẻ AM ⊥ BC (M ∈ BC) và CN ⊥ BA (K ∈ BA)
Chứng minh rằng: ∆BAM = ∆BCN
Gọi O là giao điểm của AM và CN. 
Chứng minh rằng: ∆NOA = ∆MOC
Chứng minh rằng: BO là phân giác của ABC
Lấy điểm H sao cho AC là trung trực của đoạn thẳng OH. Tìm điều kiện của ∆ABC để ∆OCH đều.
TRƯỜNG THCS MAI ĐỘNG KIỂM TRA TOÁN 7
 -------------- Thời gian: 45 phút
 ĐỀ SỐ 2
Bài 1: Đánh dấu x vào ô thích hợp
Khẳng định
Đúng
Sai
1. Một tam giác cân có góc ở đỉnh là 400 thì góc ở đáy có số đo là 700
2. Tam giác cân có góc ở đáy là 450 thì tam giác đó vuông cân
3. Góc ở đỉnh của tam giác cân luôn là góc nhọn
4. Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và một góc của tam giác kia thì hai tam giác đó bằng nhau
Bài 2: Điền giá trị thích hợp vào chỗ trống ()
 x
 800 350
 1100
 x
 12 x
 5
 24 x
 26
x = ..
x = 
x = 
x = 
Bài 3: Có tam giác vuông nào có độ dài ba cạnh như sau không? Tại sao?
12cm; 15cm; 9cm 
8m; 9m; 10m
Bài 3: Cho tam giác ABC cân có AB = AC = 10cm, BC = 12cm. Kẻ AH vuông góc với BC tại H.
Chứng minh H là trung điểm BC và tính độ dài BC.
Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN. Chứng minh rằng tam giác AMN cân.
Từ B kẻ BE vuông góc với AM tại E, từ C kẻ CF vuông góc với AN tại F. Chứng minh 
Gọi K là giao điểm của BE và CF. Chứng minh A, H, K thẳng hàng.
TRƯỜNG THCS MAI ĐỘNG KIỂM TRA TOÁN 7
 -------------- Thời gian: 45 phút
 ĐỀ SỐ 3
Bài 1: Đánh dấu x vào ô thích hợp
Khẳng định
Đúng
Sai
1. Trong một tam giác cân, nếu góc ở đỉnh bằng 800 thì góc ở đáy của tam giác cân đó là 1000
2. Tam giác vuông có một góc là 450 thì tam giác đó vuông cân
3. Trong một tam giác, góc lớn nhất là góc tù.
4. Nếu hai tam giác có ba góc bằng nhau từng đôi một thì hai tam giác đó bằng nhau.
Bài 2: Điền giá trị thích hợp vào chỗ trống ()
Tam giác vuông có độ dài hai cạnh góc vuông là 3cm và 4cm thì độ dài cạnh huyền của tam giác đó là...............
Tam giác cân có một góc bằng ............. thì tam giác đó là tam giác đều.
Bài 3: Cho tam giác ABC nhọn, kẻ AH ⊥ BC. Tính độ dài BC biết AB = 13cm, AC = 9cm, AH = 5cm (Kết quả làm tròn đến số thập phân thứ nhất).
Bài 4: Cho tam giác ABC cân tại A, lấy M là trung điểm của BC.
Chứng minh AM vuông góc với BC
Kẻ ME vuông góc với AB tại E, MF vuông gióc với AC tại F. Chứng minh rằng ME = MF.
Chứng minh rằng EF//BC
Tia EM cắt AC tại K. Tia FM cắt AB tại H. Tìm điều kiện của tam giác ABC để tam giác AHK đều.
TRƯỜNG THCS MAI ĐỘNG KIỂM TRA TOÁN 7
 -------------- Thời gian: 45 phút
 ĐỀ SỐ 4
Bài 1: Đánh dấu x vào ô thích hợp
Khẳng định
Đúng
Sai
1. Trong một tam giác cân, nếu góc ở đỉnh bằng 300 thì góc ở đáy của tam giác cân đó là 750
2. Tam giác có hai góc là 600 thì tam giác đó là tam giác đều.
3. Trong một tam giác, góc lớn nhất là góc vuông.
4. Nếu hai góc và một cạnh của tam giác này tương ứng bằng hai góc và một cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Bài 2: Điền giá trị thích hợp vào chỗ trống ()
Tam giác vuông có độ dài hai cạnh góc vuông là 6cm và 8cm thì độ dài cạnh huyền của tam giác đó là...............
Tam giác vuông có một góc nhọn bằng ............. thì tam giác đó là tam giác vuông cân.
Bài 3: Cho tam giác DEF cân có DE = DF = 5cm, EF = 8cm. Kẻ DK ⊥ EF tại F. 
Chứng minh rằng KE = KF
Tính độ dài DK
Bài 4: Cho tam giác ABC vuông tại B, kẻ AI là tia phân giác của góc BAC, IH ⊥ AC tại H.
Chứng minh 
HI cắt AB tại K. Chứng tỏ rằng BK = HC
Chứng minh rằng BH//KC
Qua C kẻ đường thẳng song song với HK, cắt AI tại O. Tìm điều kiện của tam giác ABC để tam giác CIO đều.