Kiểm tra tiết 54 - Năm học 2013 - 2014 môn: Hình học - Lớp : 8 thời gian làm bài : 45 phút

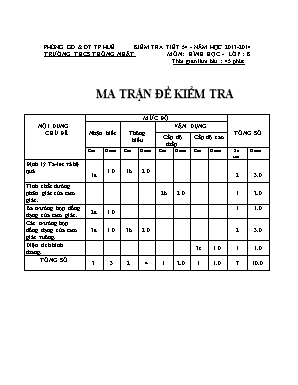
PHÒNG GD & ĐT TP HUẾ KIỂM TRA TIẾT 54 - NĂM HỌC 2013-2014
TRƯỜNG THCS THỐNG NHẤT MÔN: HÌNH HỌC - LỚP : 8 
	 Thời gian làm bài : 45 phút 
MA TRẬN ĐỀ KIỂM TRA
NỘI DUNG
 CHỦ ĐỀ
MỨC ĐỘ
TỔNG SỐ
Nhận biết
Thông hiểu
VẬN DỤNG
Cấp độ thấp
Cấp độ cao
Câu
Điểm
Câu 
Điểm
Câu
Điểm
Câu
Điểm
Số câu
Điểm
Định lý Ta-let và hệ quả
1a
1.0
1b
2.0
2
3.0
Tính chất đường phân giác của tam giác.
2b
2.0
1
2.0
Ba trường hợp đồng dạng của tam giác.
2a
1.0
1
1.0
Các trường hợp đồng dạng của tam giác vuông.
3a
1.0
3b
2.0
2
3.0
Diện tích hình thang.
3c
1.0
1
1.0
TỔNG SỐ
3
3
2
4
1
2.0
1
1.0
7
10.0
PHÒNG GD & ĐT TP HUẾ KIỂM TRA TIẾT 54 - NĂM HỌC 2013-2014
TRƯỜNG THCS THỐNG NHẤT MÔN: HÌNH HỌC - LỚP : 8 
	 Thời gian làm bài : 45 phút 
ĐỀ KIỂM TRA SỐ: .
Bài 1. (3.0 điểm) 
a) Cho AB = 6cm , AC =18cm.Tính tỉ số hai đoạn thẳng AB và AC 
b) Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:
* AB = 7cm và CD = 14cm
* MN = 20cm và PQ = 10cm
Bài 2. (3.0 điểm) Cho ABC vuông tại A , AB = 6 cm ; AC = 8 cm , BD là phân giác của ∆ABC ( D AC ).
 Tính độ dài cạnh BC , DA, DC
Vẽ đường cao AH của ABC;H ∈BC .
 Chứng minh AB2 = BH .BC.
Bài 3. (4 điểm)
 Cho tam giác MNP vuông ở M và có đường cao MK;(K∈NP) 
a) Chứng minh ∆KNM ∆MNP
b) Chứng minh MN2 = NK . NP
c) Giả sử ∆NMP vuông cân tại M. Qua P kẻ PE//KM; ( E ∈NM ),biết NK = 4cm. Tính diện tích hình thang vuông KMEP.
PHÒNG GD & ĐT TP HUẾ KIỂM TRA TIẾT 54 - NĂM HỌC 2013-2014
TRƯỜNG THCS THỐNG NHẤT MÔN: HÌNH HỌC - LỚP : 8 
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ KIỂM TRA SỐ: .
( Đáp án này gồm 03 trang )
BÀI
CÂU
NỘI DUNG
ĐIỂM
1
3.0
a
ABAC=618= 13
1.0
b
ABCD=714= 12
MNPQ=2010=2
1.0
1.0
2
3.0
a
* Tính độ dài cạnh BC , DA, DC
*ABC vuông tại A theo định lí py- ta –go, ta có: 
BC = 
*ABC có BD là tia phân giác của ∆ABC, nên:
DADC= BABC (tính chất đường phân giác trong tam giác )
0.25
0.25
0.25
0.25
b
*Ta có: AH ⊥BC, nên △HBA vuông tại H.
Hai tam giác vuông ABC và HBA có ABC chung.
Do đó: △ABC △HBA (g.g )
Suy ra: ABHB=BCBA
Hay: AB2=HB⋅BC
0.5
0.5
0.5
0.5
 3
4.0
a
 *△KNM và △MNP có:
NKM = NMP = 900
N : Góc chung
Suy ra: △KNM △MNP ( g.g )
0.25
 0.25
0. 5
b
*△KNM △MNP ( Chứng minh trên)
Nên: NMNP= KNMN
Hay: MN2=KN ⋅NP
0.5
0.5
1.0
c
*∆NMP vuông cân tại M ⟹N =450
 *∆NMK vuông tại K, 
 có N =450,
 nên ∆NMK vuông cân tại K
 Do đó: KM= KN= 4 (cm )
*∆NMP cân tại M ⟹ Đường cao MK xuất phát từ đỉnh M vừa là đường trung trực , nên :
KP= KN= 4 (cm )⟹NP=8 (cm ).
*Lại có:PE//MK và MK ⊥ NP
 Nên PE ⊥ NP.
*∆NPE vuông tại P, có N =450
Suy ra: ∆NPE vuông cân tại P
Cho nên: PE= PN= 8 (cm )
Gọi S là diện tích hình thang vuông KMEP, ta có:
S= (KM+PE)∙KP2
 = (4+8)∙42
 = 12. 2
 = 24 (cm2)
0.25
0.25
 0.25
0.25
DUYỆT CỦA TỔ TRƯỞNG 
 TỔ TOÁN-LÝ- TIN GIÁO VIÊN SOẠN
 NGUYỄN VĂN CHƠN HOÀNG TRỌNG LÂM