Kiểm tra học kì II – Năm học 2015 – 2016 môn: Toán 9 thời gian làm bài: 90 phút (không kể giao đề)

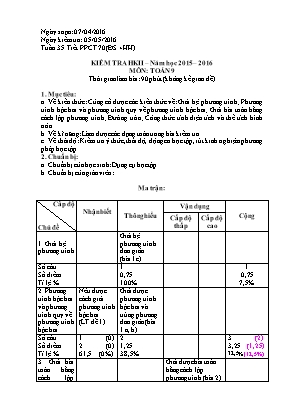
Ngày soạn: 07/04/2016
Ngày kiểm tra: 05/05/2016.
Tuần 35. Tiết PPCT 70 (ĐS +HH)
KIỂM TRA HKII – Năm học 2015 – 2016 
MÔN: TOÁN 9
Thời gian làm bài: 90 phút (không kể giao đề)
1. Mục tiêu:
a. Về kiến thức: Củng cố được các kiến thức về: Giải hệ phương trình; Phương trình bậc hai và phương trình quy về phương trình bậc hai; Giải bài toán bằng cách lập phương trình; Đường tròn; Công thức tính diện tích và thể tích hình nón. 
b. Về kĩ năng: Làm được các dạng toán trong bài kiểm tra
c. Về thái độ: Kiểm tra ý thức, thái độ, động cơ học tập, rút kinh nghiệm phương pháp học tập.
2. Chuẩn bị:
a. Chuẩn bị của học sinh: Dụng cụ học tập
b. Chuẩn bị của giáo viên: 
Ma trận:
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Giải hệ phương trình
Giải hệ phương trình đơn giản
(bài 1c)
Số câu 
Số điểm 
Tỉ lệ %
1
0,75
100%
1
0,75
7,5%
2. Phương trình bậc hai và phương trình quy về phương trình bậc hai
Nêu được cách giải phương trình bậc hai
(LT đề 1)
Giải được phương trình bậc hai và trùng phương đơn giản (bài 1 a, b)
Số câu 
Số điểm 
Tỉ lệ %
1 (0)
2 (0)
61,5 (0%)
2
1,25
38,5%
3 (2)
3,25 (1,25)
32,5%(12,5%)
3. Giải bài toán bằng cách lập phương trình
Giải được bài toán bằng cách lập phương trình (bài 2)
Số câu 
Số điểm 
Tỉ lệ %
1
2
100%
1
2
20%
4. Góc nội tiếp
 Nêu được tính chất góc nội tiếp(LT đề 2)
Áp dụng tính được số đo cung(LT đề 2)
Số câu 
Số điểm 
Tỉ lệ %
(0) (1)
(0) (1)
(0) (50%)
(0) (1)
(0) (1)
(0) (50%)
(0) (2)
(0) (2)
(0) (20%)
5. Tứ giác nội tiếp
Chứng minh được tứ giác nội tiếp (Bài 3 a) GT, KL, Hình
Số câu 
Số điểm 
Tỉ lệ %
1
1
100%
1
1
10%
6. Tính chất hai tiếp tuyến cắt nhau
Vận dụng tính chất tiếp tuyến cắt nhau làm bài tập (Bài 3 b)
Số câu 
Số điểm 
Tỉ lệ %
1
1
100%
1
1
10%
7. Trường hợp đồng dạng thứ ba
Vận dụng tam giác đồng dạng chứng minh hệ thức (bài 3 c)
Số câu 
Số điểm 
Tỉ lệ %
1
1
100%
1
1
10%
8. Hình nón
Vận dụng công thức tính diện tích và thể tích hình nón (bài 4)
Số câu 
Số điểm 
Tỉ lệ %
1
1
100%
1
1
10%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
1 (1)
2 (1)
20% (10%) 
3 (4)
2 (3)
20% (30%)
5 
6 
60% 
9 (10)
10 (10)
100%
Đề bài:
I - LÝ THUYẾT: (2 điểm) Học sinh chọn một trong hai đề sau :
Đề 1 : Viết công thức nghiệm của phương trình bậc hai.
Đề 2 : a) Nêu tính chất góc nội tiếp. 
	 b) Áp dụng: cho biết góc BAC = 300. Tính số đo cung BC?
II - BÀI TẬP : (8 điểm) 
Bài 1. (2 điểm) 
 Giải phương trình và hệ phương trình sau :
	a) x2 + 5x – 6 = 0 	b) 2x4 + 3x2 – 2 = 0	c) 
Bài 2. (2 điểm) Một xe khách và một xe du lịch khởi hành đồng thời từ A đến B. Xe du lịch có vận tốc lớn hơn xe khách là 20 km/h do đó đến B trước xe khách 50 phút. Tính vận tốc mỗi xe. Biết khoảng cách từ A đến B là 100 km.
Bài 3. (3 điểm) Cho nửa đường tròn (O ; R) đường kính AB cố định. Qua A và B vẽ các tiếp tuyến với nửa đường tròn tâm O. Từ một điểm M tùy ý trên nửa đường tròn (M A, M B) vẽ tiếp tuyến thứ 3 với nửa đường tròn cắt các tiếp tuyến tại A và B theo thứ tự là H và K.
	a) Chứng minh tứ giác AHMO là tứ giác nội tiếp.
	b) Chứng minh AH + BK = HK.
	c) Chứng minh ∆HAO ∆AMB và HO . MB = 2R2
Bài 4. (1 điểm) Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4 cm, góc ACB bằng 300. Tính diện tích xung quanh và thể tích hình nón.
Đáp án – Thang điểm
 Câu
Nội dung
Điểm
LÝ THUYẾT
LT
Đề 1
Viết đúng công thức nghiệm của PT bậc hai (sgk)
2
LT
Đề 2
Nêu tính chất góc nội tiếp (sgk)
Số đo cung BC = 600
1
1
BÀI TẬP
Bài 1
a) x2 + 5x – 6 = 0 có a + b + c = 1 + 5 + (-6) = 0	
Nên phương trình có 2 nghiệm là: x1 = 1 ; x2 = -6
0,25
0,25
b) 2x4 + 3x2 – 2 = 0 (2)
Đặt x2 = t ≥ 0 phương trình (2) trở thành
2t2 + 3t – 2 = 0
∆ = 25
t1 = (nhận)
t2 = -2 (loại)
Với t = t1 = , ta có x2 = . Suy ra x1 = , x2 = -
0,25
0,25
0,25
c) 
0,25
0,25
0,25
Bài 2
Gọi vận tốc của xe khách là x (km/h); ĐK: x > 0
Vận tốc xe du lịch là: x + 20 (km/h)	
Thời gian xe khách đi hết quãng đường là: (h)
Thời gian xe du lịch đi hết quãng đường là: (h)
Đổi 50 phút = h
Theo bài ta có phương trình : - = 	 600 (x + 20) – 5x (x + 20) = 600x
600x + 12 000 – 5x2 – 100x – 600x = 0
5x2 + 100x – 12 000 = 0
 x2 + 20x – 2 400 = 0	102 + 2 400 = 2 500
 = 50 => x1 = = 40
	 => x2 = = -60 	 (loại)
Vậy vận tốc xe khách là: 40 km/h 
 và vận tốc xe du lịch là: 60 km/h	
0,25
0,25
0,25
0,5
0,25
0,25
0,25
Bài 3
Vẽ hình ghi GT, KL
0,5
a) Chứng minh tứ giác AHMO là tứ giác nội tiếp
	Xét tứ giác AHMO có:
	 = = 900 (tính chất tiếp tuyến)	+ = 1800
nên tứ giác AHMO nội tiếp đường tròn.	
b) Chứng minh AH + BK = HK
	Theo tính chất hai tiếp tuyến cắt nhau 
	Ta có: AH = MH và MK = KB	Mà HM + MK = HK (vì M nằm giữa H và K)
AH + BK = HK	
c) (g g)
 HO . MB = AB . AO = 2R2 
0,5
0,5
0,5
0,5
0,5
Bài 4
AB = 2 cm
AC = cm
Sxq = 8 cm2
V = cm3
0,25
0,25
0,25
0,25
Học sinh giải theo cách khác đúng vẫn cho điểm tối đa
3. Tiến trình tổ chức kiểm tra:
a. Ổn định lớp:
b. Tổ chức kiểm tra:
 Phát đề, HS làm bài, GV giám sát làm bài ; Thu bài
c. Dặn dò: Xem lại kiến thức
d. Rút kinh nghiệm và bổ sung ý kiến của đồng nghiệp hoặc của cá nhân:
	Giáo viên ra đề
	Võ Minh Mẫn
Phòng GD&ĐT Hòn Đất	KIỂM TRA HỌC KÌ II – Năm học: 2015 – 2016
	Trường THCS Bình Giang 	Môn: Toán. Khối: 9 
Lớp 9/ 	Thời gian 90 phút (không kể giao đề)
Họ và tên: ..............................................
Điểm 
Lời nhận xét 
Đề bài
	I - LÝ THUYẾT: (2 điểm) Học sinh chọn một trong hai đề sau :
Đề 1 : Viết công thức nghiệm của phương trình bậc hai.
Đề 2 : a) Nêu tính chất góc nội tiếp. 
	 b) Áp dụng: cho biết góc BAC = 300. Tính số đo cung BC?
II - BÀI TẬP : (8 điểm) 
Bài 1. (2 điểm) 
 Giải phương trình và hệ phương trình sau :
	a) x2 + 5x – 6 = 0 	 b) 2x4 + 3x2 – 2 = 0	c) 
Bài 2. (2 điểm) Một xe khách và một xe du lịch khởi hành đồng thời từ A đi đến B. Xe du lịch có vận tốc lớn hơn xe khách là 20 km/h do đó đến B trước xe khách 50 phút. Tính vận tốc mỗi xe. Biết khoảng cách từ A đến B là 100 km.
Bài 3. (3 điểm) Cho nửa đường tròn (O ; R) đường kính AB cố định. Qua A và B vẽ các tiếp tuyến với nửa đường tròn tâm O. Từ một điểm M tùy ý trên nửa đường tròn (M A, M B) vẽ tiếp tuyến thứ 3 với nửa đường tròn cắt các tiếp tuyến tại A và B theo thứ tự là H và K.
a) Chứng minh tứ giác AHMO là tứ giác nội tiếp.
	b) Chứng minh AH + BK = HK.
	c) Chứng minh ∆HAO ∆AMB và HO . MB = 2R2
Bài 4. (1 điểm) Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4 cm, góc ACB bằng 300. Tính diện tích xung quanh và thể tích hình nón.
HẾT
Bài làm