Kiểm tra 1 tiết chương III môn: Toán hình học 8 thời gian: 45 phút

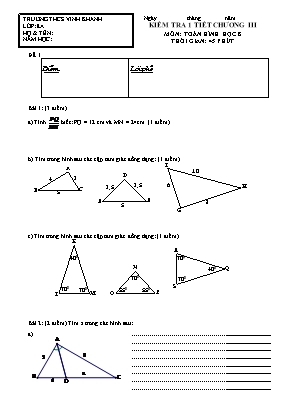
TRƯỜNG THCS VĨNH KHÁNH
LỚP: 8A
HỌ & TÊN:
NĂM HỌC: ...
	Ngàythángnăm .
	KIỂM TRA 1 TIẾT CHƯƠNG III
	MÔN: TOÁN HÌNH HỌC 8
	THỜI GIAN: 45 PHÚT
ĐẾ 1
Điểm
Lời phê
Bài 1: (3 điểm)
a) Tính biết: PQ = 12 cm và MN = 24cm. (1 điểm)
I
10
A
b) Tìm trong hình sau các cặp tam giác đồng dạng: (1 điểm)
D
4
3
H
3,5
3,5
5
6
B
C
F
E
8
G
5
K
c) Tìm trong hình sau các cặp tam giác đồng dạng: (1 điểm)
700
R
400
400
Q
N
700
700
S
550
550
700
700
P
O
M
L
Bài 2: (2 điểm) Tìm x trong các hình sau:
a)
b) 
 DE // BC
Bài 3: (4,0 điểm) Cho vuông tại M. Trên tia MP lấy điểm A. Từ A kẻ đường thẳng vuông góc với PQ tại B cắt MQ tại C.
	a) Chứng minh: MPQ BPA (1,5 điểm)
	b) Chứng minh: BC . CA = MC . CQ (1 điểm)
	c) Giả sử BQ = 8cm, AB = 4cm, AC = 2cm. Tính MC? (1 điểm)
 (Chú ý vẽ hình 0,5 điểm)
Bài 4: (1,0đ) Bóng của một cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó, một thanh sắt cao 2m cắm vuông góc với mặt đất có bóng dài 1,5m. Tính chiều cao của cột điện đó?
(Cho biết những tia sáng song song với nhau).
A
B
C
4,5
E
F
D
1,5
2
HẾT.ĐÁP ÁN
Bài
Đáp án
Điểm
1
(3 điểm)
a) 
b) ABC GHI (c-c-c)
c) KLM QRS (g-g)
1
1
1
2
(2 điểm)
a) Theo tính chất đường phân giác của tam giác ta có:
b) Theo định lí Ta-let ta có:
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
3
(4,0 điểm)
0,5
a) Xét MPQ vàBPA ta có: 
 là góc chung
Vậy: MPQ BPA (g.g)
(hs chứng minh theo trường hợp hai tam giác vuông đồng dạng cũng tính đúng)
0,25
0,25
0,25
0,5
0,25
b) Xét BCQ vàMCA ta có:
 là góc chung
Vậy: BCQ MCA (g.g)
 BC . CA = MC . CQ
0,25
0,25
0,25
0,25
c) Ta có: BC = AB + AC = 4 + 2 = 6 (cm)
Áp dụng định lý Pytago vào BCQ vuông tại B, ta có:
Ta có: hay 
0,25
0,25
0,25
0,25
4
(1,0 điểm)
Gọi AB là chiều cao của cột điện, AC là bóng của cột điện;
 DE là chiều cao của thanh sắt, EF là bóng của thanh sắt;
Vì tam giác vuông ABC tam giác vuông DEF (góc C = góc F do đồng vị).
Nên ta có: 
AB . 1,5 = 4,5 . 2
AB . 1,5 = 9
AB = 9 : 1,5
AB = 6 (m)
Vậy chiều cao của cột điện là 6m.
0,25
0,25
0,25
0,25
	GVBM
	 NGUYỄN NGỌC