Kì thi thử trung học phổ thông quốc gia năm 2016 môn thi: Toán (thời gian làm bài: 180 phút)

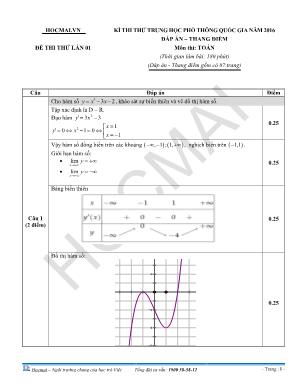
 Hocmai – Ngôi trường chung của học trò Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 1 - 
HOCMAI.VN 
KÌ THI THỬ TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2016 
ĐÁP ÁN – THANG ĐIỂM 
ĐỀ THI THỬ LẦN 01 
Môn thi: TOÁN 
(Thời gian làm bài: 180 phút) 
(Đáp án - Thang điểm gồm có 07 trang) 
Câu Đáp án Điểm 
Câu 1 
(2 điểm) 
Cho hàm số 3 3 2y x x   , khảo sát sự biến thiên và vẽ đồ thị hàm số. 
Tập xác định là D = R. 
Đạo hàm 2' 3x 3y   
2
1
' 0 1 0
1
x
y x
x

       
0.25 
Vậy hàm số đồng biến trên các khoảng  , 1  ;  1, , nghịch biến trên  1,1 . 
Giới hạn hàm số: 
 lim
x
y

  
 lim
x
y

  
0.25 
Bảng biến thiên 
0.25 
Đồ thị hàm số: 
0.25 
2
2
4
6
 Hocmai – Ngôi trường chung của học trò Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 2 - 
Câu 2 
(1 điểm) 
Viết phương trình tiếp tuyến của hàm số 
2x 1
y
x 1



. Biết tiếp tuyến qua giao điểm của đồ thị với 
trục tung. 
Ta có giao của đồ thị với trục tung là:  I 0, 1 
Phương trình tiếp tuyến của đồ thị hàm số đi qua điểm có hoành độ 
0
x có dạng: 
    
 
  00 0 0 02
00
2x 13
y y' x x x y x x x
x 1x 1

     

0.5 
Tiếp tuyến đi qua điểm  I 0, 1 nên: 
 
  00 02
00
2x 13
0 x 1 x 0
x 1x 1

     

Từ đây ta có tương ứng tiếp tuyến là: y 3x 1    
0.5 
Câu 3 
(1 điểm) 
a. Trong mặt phẳng Oxy, tìm tập hợp điểm biểu diễn các số phức thỏa mãn điều kiện: 
 3 4 2z i   . 
Gọi  ;M a b biểu thị số phức  , ,b Rz a bi a   
Ta có    3 4 3 4z i a b i      
Vậy      
2 2
3 4 2 3 4 2z i a b        
0.25 
    
2 2
3 4 4a b     
Do đó tập hợp điểm M biểu diễn các số phức z trong mặt phẳng Oxy là đường tròn tâm 
(3; 4)I  và bán kính 2R  . 
0.25 
b. Giải phương trình sau: 1
3 3log (3 1)log (3 3) 6
x x   
ĐK: 
3
03 1 0
log 23 1 1
x
x
x
x
   
 
  

  13 3
3 3
1
3
2
1 3
2 3
1 log (3 1) log (3 3) 6
log (3 1) 1 log (3 1) 6
3
log (3 1) ( 1) 6
2
28
log .
27
log 10.
   
      
 
      





x x
x x
x
t
t t t
t
x
x
0.5 
Câu 4 
(1 điểm) 
Tính diện tích hình phẳng giới hạn bởi các đường : 
ln
1; ; 0; 1
x
x x e y y
x
     
Gọi S là diện tích cần xác định, ta có: 
1
ln
1
e
x
S dx
x
  0.5 
 Hocmai – Ngôi trường chung của học trò Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 3 - 
Bởi  
ln ln
1; ln 0 1 1
x x
x e x
x x
       
Do đó:  
1
1 1 1
ln ln ln
1 1
e e e
ex x x
S dx dx x dx e
x x x
 
       
 
   
Đặt 
ln
2
dxu x
du
xdx
dv
v xx
 
 
 
   
Khi đó: 
       
1
2
1 2 ln 1 2 ln 4 3 2
1 1
ee ex
S e x x dx e x x x e e
x
           (đvdt) 
0.5 
Câu 5 
(1 điểm) 
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( ) : 2x y 2z 1 0     và đường thẳng 
y 1x 1 z
d :
1 2 2

 

. Viết phương trình mặt cầu có tâm thuộc d, tiếp xúc với hai mặt phẳng ( ) và 
Oxy . 
 Gọi I là tâm mặt cầu (S) cần tìm, vì    I d I t 1; 2t 1; 2t     . 
Theo giả thiết mặt cầu (S) tiếp xúc với mặt phẳng ( ) và Oxy nên I cách đều hai mặt phẳng 
này, do đó: 
   
     
d I,(Oxy) d I,( )
2 t 1 2t 1 2 2t 1 2 4t
2t
34 1 4
t 12 4t
2t 1
3 t
5
 
      
   
 
  
    
 

0.5 
Do đó ta có 2 điểm I là: 
+)  t 1 I 0; 1; 2    
+) 
1 6 7 2
t I ; ;
5 5 5 5
 
   
 
Vậy có hai mặt cầu thỏa mãn đề bài: 
• Mặt cầu 1( )S có tâm 1(0; 1;2)I , bán kính 1R z 2  
  2 2 21S : x (y 1) (z 2) 4     
•Mặt cầu (S2) có tâm 2
6 7 2
I , ,
5 5 5
  
 
 
, bán kính 2
2
R z
5
  
(S2): 
2 2 2
6 7 2 4
x y z
5 5 5 25
     
          
     
. 
0.5 
 Hocmai – Ngôi trường chung của học trò Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 4 - 
Câu 6 
(1 điểm) 
a. Giải phương trình 2 2cos 6cos 6cos sin 1 0x x x x    trên đoạn  0; 
 Phương trình 2 2cos 6cos 6cos sin 1 0x x x x    
3 2
2
6cos cos 1 0
(2cos 1)(3cos 2cos 1) 0
x x
x x x
   
    
0.25 
1
cos
2
x  
  2 ,
3
x k k    

 
Như vậy nghiệm của PT trên đoạn  0; là: 
3

0.25 
b. Trong 1 lớp học có 6 bóng đèn, năm bóng có xác suất bị cháy là 
1
4
. Lớp học đủ sáng nếu có ít 
nhất 4 bóng sáng. Tìm xác suất để lớp học đủ ánh sáng. 
Ta đi tìm xác xuất để lớp học không đủ sáng: 
+ Xác suất 3 bóng cháy : 
3
3
5
1
.
4
C
 
 
 
+ Xác suất 4 bóng cháy : 
4
4
5
1
.
4
C
 
 
 
+ Xác xuất 5 bóng đều cháy: 
5
5
5
1
.
4
C
 
 
 
0.25 
Vậy xác suất để lớp học không đủ sáng là : 
3 4 5
5 5 5
1 3 4 54 4 4
C C C
p    
Do đó xác suất để lớp học đủ sáng là : 2 1
845
1
1024
p p   
0.25 
Câu 7 
(1 điểm) 
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = a. Gọi I là giao điểm 
của AB’ và A’B. Tính thể tích của khối tứ diện ACA’B’ và khoảng cách giữa hai đường thằng AB 
và CI. 
 Hocmai – Ngôi trường chung của học trò Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 5 - 
Gọi V là thể tích của lăng trụ ABC.A’B’C’ ta có: 
' ' '. ' '. ' '
1
2
ACA B B ACA B ACC AV V V 
'.
1 1 1 1 2 1
( ) ( ) .
2 2 3 2 3 3
B ABCV V V V V V      
2 21 1 3 3
. .AA' . .
3 3 4 12
ABC
a a
S a   
0.5 
Gọi E là trung điểm của AB => CE  AB (1) 
IE là đường trung bình của tam giác ABB’=> IE // BB’ 
Mà BB’ AB => IE AB (2) 
Từ (1) và (2) => AB  (CIE). 
Trong mặt phẳng ( )CIE kẻ EK IC 
=> EK là đoạn vuông góc chung của AB và IC. Suy ra: ( , )d AB IC IK . 
Ta có: 
3 1
; AA'=
2 2 2
a a
EC EI  
Xét tam giác vuông CEI có: 
2 22 2 2 2 2 2
1 1 1 1 1 4 4 16 3
3 3 43
2 2
a
EK
EK EI EC a a aa a
        
   
   
    
Vậy khoảng cách giữa hai đường thẳng AB và IC bằng 
3
4
a
. 
0.5 
Câu 8 
(1 điểm) 
Trong mặt phẳng hệ tọa độ Oxy, cho hình thang cân ABCD có 
45
2
ABCDS  , đáy lớn CD nằm trên 
đường thẳng 3 3 0x y   Biết 2 đường chéo AC, BD vuông góc với nhau tại (2;3)I . Viết 
phương trình cạnh BC, biết điểm C có hoành độ dương. 
Gọi M, N lần lượt là trung điểm của CD, AB 
Do AC BD =>Tam giác AIB và CID là 2 tam giác vuông 
 cân tại I => ,   IN NA NB IM MC MD 
+  , 10 2 10I CDd CD   
+ 2NI x AB x   
0.5 
I
A'
B'
C'
C
B
A
H
E
K
 Hocmai – Ngôi trường chung của học trò Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 6 - 
    
 
 
2
2 2 10 10
2 2
45
10
2
10 1
*
2 2
ABCD
x xAB CD MN
S
x
IN IB
x
IM ID
 
 
  
    
+ MN qua I vuông góc với CD => MN: 3 9 0x y   
 Toạ độ M là nghiệm của hệ:  
3 9 0
3;0
3 3 0
M
x y
x y

  
  
+ PT đường tròn tâm M bán kính MI:    
2 2: 3 10C x y   
+ C, D là giao điểm của đường tròn  C với đường DC. 
   
 
2 2 0; 13 10
6;0 13 3x y
Dx y
C


  
 
   
 (do 0Cx  )
+ Từ (*)  2 3,5DI IB B   =>PT đường thẳng qua B, C là : 4 3 27 0x y   
0.5 
Câu 9 
(1 điểm) 
Giải phương trình   33 2 3 2 1 3 7 6
3 2
x x
x
    

Điều kiện 
2
3
x  
  3 33 7 62 3 2 1 3 7 6 2 3 2 3 7 6
3 2 3 2
x
x x x x
x x

         
 
Đặt 
3
2
3 2,
3
7 6
a x a
b x

  

  
Khi đó ta có hệ phương trình: 
 
 
3
2
2 3
2 3 1
2 3 2
b
a b
a
a b

 

  
0.5 
     
3
2
2
1 2 3 2 0
2
b ab
a b a b a b
b aa

          
+) Với a b 3 22 3 0 1 1a a a x        
+) Với 2b a  , ta có    
32 3 22 2 3 8 2 3 0 *a a a a        
Vì 0a  nên áp dụng Cosi cho 3 số 3 3; ;1a a ta có: 
3 3 2 3 2 3 21 3 2 1 3 2 1 2a a a a a a a         
Từ đây suy ra (*) vô nghiệm 
Vậy phương trình ban đầu có nghiệm duy nhất là: 1x  
0.5 
N
I
A
B
D
C
M
 Hocmai – Ngôi trường chung của học trò Việt Tổng đài tư vấn: 1900 58-58-12 - Trang | 7 - 
Nguồn: Hocmai.vn 
Câu 10 
(1 điểm) 
Cho , 0x y  thoả mãn 
1 1 1
3
x y xy
   . Tìm giá lớn nhất của: 
   2 2
3 1 3 3 1 3
1 1
P
y y y x x x x y
     
 
Đặt , , 0; a x y b xy a b     
Từ 
1 1 1 1
3 1 3 1 3 ; 0 3 1 0
3
x y xy a b a b b
x y xy
                
    
22 a 4 3 1 4 9 1 1 0 1b b b b b b          
Ta có: 
   
  
2 2 2 2
2 2
3 1 3 1
1 1
x y y x x y
P
xy x y x y
   
 
 
   
 
 
2 2
2 2
3 3 6 2
1
xy x y x y xy x y xy
xy xy x y x y
     
 
  
 
2 2
2
3 3 6 2
1
ab a b a b
b b a b
  
 
 
   
 
 
2 2
2
3 3 1 3 3 1 6 3 1 2
3
b b b b b b
b b b b
     
 

2 2 2
2 2
9 3 27 18 3 6 36 32 4
4 4
b b b b b b b
b b
      
  
2 2
5 1 5 1
4 4 4
b
b b b

   
0.5 
Xét 
2
5 1
( ) , 1
4 4
f t t
t t
   
     2 3 3
5 1 2 5
' 0, 1 Max 
4 2 4
5 1
1 1
4 4
t
f t t t ff
t t t

            
Vậy Max 1P  dấu “=” xảy ra tại 
1 1 1
3, 11 x y
x y xy
xy       
0.5