Giáo án lớp 9 môn Toán - Tiết 69: Kiểm tra viết học kỳ II

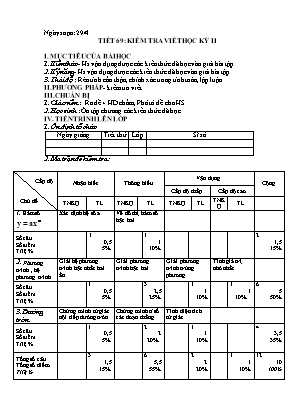
Ngày soạn: 29/4
TIẾT 69: KIỂM TRA VIẾT HỌC KỲ II
I. MỤC TIÊU CỦA BÀI HỌC
1. Kiến thức- Hs vận dụng được các kiến thức đã học vào giải bài tập
2. Kỹ năng- Hs vận dụng được các kiến thức đã học vào giải bài tập
3. Thái độ : Rèn tính cẩn thận, chính xác trong tính toán, lập luận
II. PHƯƠNG PHÁP- kiểm tra viết
III. CHUẨN BỊ
1. Giáo viên : Ra đề + HD chấm, Phô tô đề cho HS.
2. Học sinh : Ôn tập chương các kiến thức đã học
IV. TIẾN TRÌNH LÊN LỚP
1. Ổn định tổ chức 
Ngày giảng
Tiết thứ
Lớp
Sĩ số
2. Ma trận đề kiểm tra:
 Cấp độ
 Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1. Hàm số
 y = ax
Xác định hệ số a
Vẽ đồ thị hàm số bậc hai
Số câu
Số điểm
Tỉ lệ %
1
0,5 
5%
1
1 
10%
2
1,5 
15%
2. Phương trình , hệ phương trình
Giải hệ phương trình bậc nhất hai ẩn
Giải phương trình bậc hai 
Giải phương trình trùng phương
Tính giá trị nhỏ nhất 
Số câu
Số điểm
Tỉ lệ %
1
0,5 
5%
3
2,5
25%
1
1
10%
1
1
10%
6
5
50%
3. Đường tròn
Chứng minh tứ giác nội tiếp đường tròn
Chứng minh tỉ số các đoạn thẳng
Tính diện tích tứ giác
Số câu
Số điểm
Tỉ lệ %
1
0,5 
5%
2
2 
20%
1
1
10%
4
3,5
35%
Tổng số câu
Tổng số điểm
Tỉ lệ %
3
1,5
15%
6
5,5
55%
2
2
20%
1
1
10%
12
10 
100%
ĐỀ KIỂM TRA HỌC KỲ II
Bài 1: (2,5 điểm) Giải phương trình và hệ phương trình sau
Bài 2: (1,5 điểm): Cho parabol (P): y = ax2 và điểm A(-2; -1). Tìm a và vẽ (P), biết (P) đi qua A
Bài 3: (2,5 điểm): Cho phương trình 
a) Chứng tỏ phương trình có nghiệm với mọi m
b) Không giải phương trình hãy tính theo m
c) Tính giá trị nhỏ nhất của A và giá trị tương ứng của m
Bài 4 (3,5 điểm): Cho tam giác ABC nhọn nội tiếp (O; R) (AB < AC). Ba đường cao AD, BE, CF gặp nhau tại H.
a) Chứng minh tứ giác BFEC nội tiếp được. Xác định tâm I của đường tròn này.
b) Tiếp tuyến tại A của (O) cắt BC kéo dài tại M. Chứng minh: MA2 = MB.MC
c) AO cắt (O) tại K. Chứng minh EF.AK = AH.BC
d) Gọi J là trung điểm của AH. Tính diện tích tứ giác JEIF theo R khi góc BAC = 450
3. Đáp án và thang điểm:
Câu
Đáp án
Điểm
1
0,25
0,25
0,5
0,5
 đặt 
0,25
Giải pt tìm được: t1 = - 1 (loại); t2 = 17/13 (thỏa mãn)
0,5
Với t2 = 17/13 => x2 = 17/13 
0,25
2
Vì Parabol (P) qua A nên tọa độ của A thỏa mãn (P)
0,5
Lập bảng giá trị:
x
-2
-1
0
1
2
-1
-1/4
0
-1/4
-1
0,5
Vẽ Parabol (P):
0,5
3
a) Ta có 
0,25
 , do đó pt có nghiệm với mọi m
0,25
b) Theo Vi-ét ta có: (*)
0,5
Ta có: (**)
Thay (*) vào (**) ta được: 
0,5
c) Ta có 
Vậy MinA = - 8; dấu “=” xảy ra khi m – 4 = 0 => m = 4
1
4
GT; KL; vẽ hình
a) Chứng minh tứ giác BFEC nội tiếp. Xác định tâm I của đường tròn
- ta có: => 2 đỉnh E; F cùng nhìn xuống cạnh BC dưới 2 góc bằng nhau => tứ giác BFEC nội tiếp. 
0,5
- do tam giác BEC vuông tại E nên tâm của đường tròn ngoại tiếp tam giác là trung điểm của cạnh BC
- do tam giác BFC vuông tại F nên tâm của đường tròn ngoại tiếp tam giác là trung điểm của cạnh BC 
- Tâm I của đường tròn ngoại tiếp tứ giác BFEC là trung điểm của cạnh BC
0,25
b) ta có (cùng chắn cung AB)
xét tam giác MAB và tam giác MCA, ta có:
0,5
0,25
c) xét tam giác AEF và tam giác ABC ta có:
0,25
- Tứ giác BDHF nội tiếp nên (cùng phụ với góc DHF)
Mà (cùng chắn cung AC), do đó: 
Xét tam giác AFH và tam giác ACK, ta có:
0,25
Từ (1) và (2) suy ra: Đpcm
0,5
d) chứng minh JE = JF (cùng = 1/2AH) => J thuộc đường trung trực của EF (3)
chứng minh IE = IF (cùng = 1/2BC) => I thuộc đường trung trực của EF (4)
từ (3) và (4) => IJ là trung trực của cạnh FE => JI vuông góc với FE
0,25
- tứ giác JEIF có hai đường chéo vuông góc với nhau nên (*)
- tính JI: ta có: OI // AJ (cùng vuông góc với BC) (3)
 (cùng chắn cung AB)
 (cùng phụ với góc BFE)
 mà 2 góc này ở vị trí so le trong nên AM // EF
Do đó: 
Mặt khác: (4)
Từ (3) và (4) ta có tứ giác AOIJ là hình bình hành => JI = AO = R
0,25
* vuông cân đỉnh E 
Do tam giác AEF đồng dạng với tam giác ABC 
* Tính cạnh BC: , do đó tam giác BOI vuông cân tại I
0,25
Thay các giá trị vào (*) ta được: 
0,25
4. Nhắc nhở, thu bài
- Thu bài kiểm tra 
- GV nhận xét thái độ làm bài của hs
5. Hướng dẫn học sinh học và làm bài tập về nhà:
- Làm lại bài kiểm tra 
V. RÚT KINH NGHIỆM: