Giáo án lớp 9 môn Ngữ văn - Tiết 33: Kiểm tra chương 2

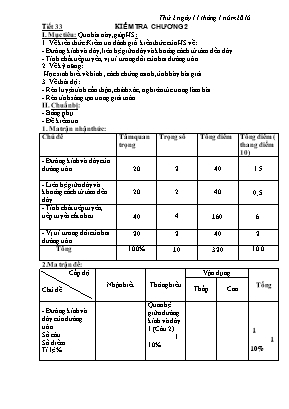
 Thứ 2 ngày 11 tháng 1 năm 2016 
Tiết 33 KIỂM TRA CHƯƠNG 2 
I. Mục tiêu: Qua bài này,giúp HS:
1. Về kiến thức: Kiểm tra đánh giá kiến thức của HS về:
- Đường kính và dây ,liên hệ giữa dây và khoảng cách từ tâm đến dây.
- Tính chất tiếp tuyến, vị trí tương đối của hai đường tròn
2. Về kỹ năng:
 Học sinh biết vẽ hình , cách chứng minh, tình bày bài giải.
3. Về thái độ:
- Rèn luyện tính cẩn thận,chính xác, nghiêm túc trong làm bài.
- Rèn tính sáng tạo trong giải toán
II. Chuẩn bị:
- Bảng phụ.
- Đề kiểm tra.
1. Ma trận nhận thức:
Chủ đề
Tầm quan trọng
Trọng số
Tổng điểm
Tổng điểm ( thang điểm 10)
- Đường kính và dây của đường tròn
20
2
40
1.5
- Liên hệ giữa dây và khoảng cách từ tâm đến dây
20
2
40
0.5
- Tính chất tiếp tuyến, tiếp tuyến cắt nhau
40
4
160
6
- Vị trí tương đối của hai đường tròn
20
2
40
2
 Tổng
100%
10
320
10.0
2.Ma trận đề:
 Cấp độ 
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
Thấp
Cao
- Đường kính và dây của đường tròn
Số câu
Số điểm 
Tỉ lệ %
Quan hệ giữa đường kính và dây
1 (Câu 2)
 1
10%
 1
 1
10% 
- Liên hệ giữa dây và khoảng cách từ tâm đến dây
Số câu
Số điểm 
Tỉ lệ %
Biết liên hệ giữa dây và khoảng cách từ tâm đến dây,vẽ hình
2 (Câu 2)
 1
10%
 2
 1
10% 
- Tính chất tiếp tuyến, tiếp tuyến cắt nhau
Số câu
Số điểm 
Tỉ lệ %
Hiểu tính chất hai tiếp tuyến cắt nhau, vẽ hình
2 (Câu 3a)
 1
10%
Vận dụng tính chất hai tiếp tuyến cắt nhau
3 (Câu 3)
 4
40%
Vận dụng tính chất hai tiếp tuyến cắt nhau
1(Câu3d)
 1
10%
6
 6
60%
- Vị trí tương đối của hai đường tròn
Số câu
Số điểm 
Tỉ lệ %
Biết hệ thức rồi suy ra vị trí
2 (câu 1a,b)
 1
10%
Biêt tính tổng, hiệu các bán kính
2 (câu 1a,b)
 1
10%
4
 2 20%
Tổng
 2
 1
10% 
7
 4
40% 
3
 4
40%
1
 1
10%
13
 10
100%
3. Đề bài:
C©u 1 (2 ®iÓm): Cho 2 ®­êng trßn (O; R) vµ (O’; r). Biết OO’ = 7cm. Cho biÕt vÞ trÝ t­¬ng ®èi cña hai ®­êng trßn (O;R) vµ (O’; r) trong các trường hợp sau,Gi¶i thÝch?
 a, R= 5cm, r= 3cm
 b, R=4cm, r=3cm
C©u 2 (2®iÓm). Cho đường tròn (O), hai dây AB,BC không đi qua tâm, H, K theo thứ tự là trung điểm của AB và BC. So sánh AB và BC nếu OH < OK.
Câu 3 ( 6 điểm) Cho ®­êng trßn (O),®­êng kÝnh AB. Vẽ các tiếp tuyến Ax, By trên cùng một nửa mặt phẳng bờ AB chứa nửa đường tròn. Vẽ bán kính OH bất kỳ. Tiếp tuyến nửa đường tròn tại H cắt Ax, By theo thứ tự tại M và N.
a,Chứng minh MN = AM+BN
b,Tính số đo của góc MON
c,Gọi I là giao điểm của OM và AH , gọi K là giao điểm của ON và BH. Tứ giác HIOK là hình gì? Vì sao?
 d,Xác định vị trí của bán kính OH để diện tích tứ giác HIOK bằng diện tích tứ giác ABNM.
4.§¸p ¸n và biểu điểm:
Câu 1. a, R-r= 2, R+r=8 nên R-r<OO’< R+r nên (O;R) cắt (O’;r) (1,0 điểm)
 b, R + r = 7 nên OO’= R + r nên (O;R) tiếp xúc ngoài (O’;r) (1,0 điểm)
Câu 2: Vẽ hình đúng (0.5 điểm)
Vì H, K là trung điểm của AB, BC nên OH^ AB, OK^ BC (1,0 điểm)
Mà OH BC (0.5 điểm)
Câu 3: Vẽ hình đúng câu a,b (0.5điểm)
a,Theo tính chất hai tiếp tuyến cắt nhau ta có AM= MH, BN=HN (0.5 diểm)
 Nên AM+BN=MH+HN=MN (1,0 điểm)
b,Theo tính chất hai tiếp tuyến cắt nhau ta có 
 OM,ON lần lượt là các tia phân giác của góc AOH và góc BOH (0.5 điểm)
 Mà góc AOH kề bù góc BOH (0.5 điểm)
 do đó góc MON băng 90 (0.5 điểm)
c,Ta có AOH cân tại O có OM là có OM là phân giác nên OM^ AH (0.25 điểm)
 suy ra , (0.25 điểm) 
tương tự (0.5 điểm)
Vậy tứ giác OIHK là hình chữ nhật. (0.5 điểm)
 d, SOIHK= SABH (0.25 điểm) 
 do đó SOIHK= SABNM (0.25 điểm) 
 Û OIHK là hình vuông (0.25 điểm) 
 Û OH^ AB . (0.25 điểm)