Giáo án lớp 12 môn Toán - Phương pháp tọa độ trong mặt phẳng

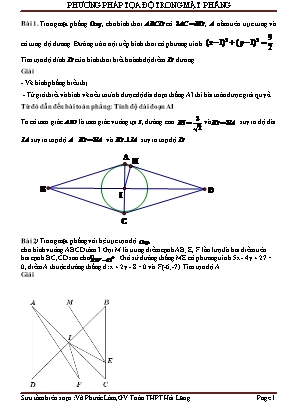
Bài 1. Trong mặt phẳng , cho hình thoi có , nằm trên trục tung và có tung độ dương. Đường tròn nội tiếp hình thoi có phương trình . Tìm tọa độ đỉnh của hình thoi biết hoành độ điểm dương.
Giải
- Vẽ hình phẳng biểu thị
 - Từ giả thiết và hình vẽ nếu ta tính được độ dài đoạn thẳng AI thì bài toán được giải quyết
Từ đó dẫn đến bài toán phẳng: Tính độ dài đoạn AI
Ta có tam giác là tam giác vuông tại, đường cao và suy ra độ dài suy ra toạ độ . và suy ra toạ độ .
Bài 2) Trong mặt phẳng với hệ trục tọa độ , 
cho hình vuông ABCD tâm I. Gọi M là trung điểm cạnh AB; E, F lần lượt là hai điểm trên hai cạnh BC, CD sao cho . Giả sử đường thẳng ME có phương trình 5x - 4y + 27 = 0, điểm A thuộc đường thẳng d: x + 2y - 8 = 0 và F(-6;-7). Tìm tọa độ A. 
Giải
Do ABCD là hình vuông nên 
Ta có 
Từ (1) và (2), suy ra DFID ∽ DIEB, suy ra 
Đặt BM = a > 0, suy ra AD = 2a, 
Ta có 
Suy ra 
Đường thẳng AF đi qua F(-6;-7) và song song ME nên AF: 5x - 4y + 2 = 0. Do A = AFÇ d nên tọa độ điểm A là nghiệm của hệ 
Vậy A(2;3).
Bài 3. (Đề thi thử THPT QG - Violet) Trong mặt phẳng với hệ trục tọa độ Oxy, cho hình vuông ABCD tâm I .Gọi M và N lần lượt là trung điểm của CD và BI .Tìm tọa độ các điểm B,C,D biết A(1;2) đường thẳng MN có phương trình và điểm M có tung độ âm 
Giải
+ Gọi J là trung điểm của AI Tứ giác DMNJ là hình bình hành 
+ Xét tam giác có J là giao điểm của hai đường cao AI và NJ nên J là trực tâm là hình chiếu của A trên MN 
+ Phương trình đường thẳng AN : 
+ Tọa độ của N là nghiệm hệ phương trình N(2;0)
+ ADMN là tứ giác nội tiếp vuông cân tại N
 .Gọi có Tìm được 
 M( 0;-1) 
 + Gọi K là giao điểm AM và BD là trọng tâm của tam giác 
 .Tìm được 
+ Ta có , B,N,I,K thẳng hàng và 
 Từ đó tìm được 
+ I là trung điểm AC nên tìm được C(1;-2)
+ M là trung điểm CD nên tìm được D(-1;0)
+ I là trung điểm BD nên tìm được B(3;0) 
Bài 4. (Đề thi thử THPT QG - Violet) Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có . là điểm nằm bên trong hình bình hành sao cho và . Tìm tọa độ điểm D biết .
Giải Gọi E là điểm thứ tư của hình bình hành MABE, dễ thấy MECD cũng 
là hình bình hành nên 
Mà suy ra hay tứ giác BECM nội tiếp. 
Suy ra 
Ta có hay vuông tại M      
Vì . 
Ta có .
Giả sử ta có .
Giải hệ phương trình trên được hai nghiệm: 
Vậy có hai điểm D thỏa mãn đề bài là: 
Bài 5. (Đề thi thử THPT QG - Violet) Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có . Một điểm M(1;-1) nằm trong hình bình hành sao cho và . Tìm tọa độ đỉnh D, biết rằng D thuộc đường tròn (T) : .
Giải
Lấy điểm E sao cho ABEM là hình bình hành Þ DCEM cũng là hình bình hành
 Þ tứ giác BECM nội tiếp mà Þ . 
DAMD = DBEC (c.c.c) Þ . Từ đó ta lập được phương trình DM là
2x - y - 3 = 0 hoặc x + 2y + 1 = 0 và tìm được các tọa độ của D là (0;-3), (-1;0), (2 ;1) và (3 ;-2) . Ta loại hai điểm do góc . Vậy D(2 ;1) hoặc D(3 ;-2)