Giáo án lớp 12 môn Toán - Chương II: Mặt nón, mặt trụ, mặt cầu

CHƯƠNG II. MẶT NÓN, MẶT TRỤ, MẶT CẦU
----- oOo -----
F CHUẨN BỊ KIẾN THỨC:
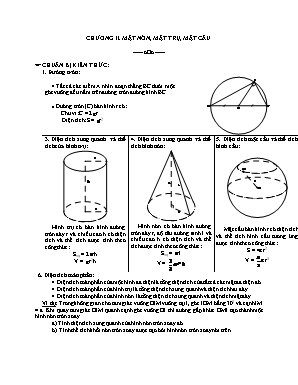
 1. Đường tròn: 
 · Tất cả các điểm A nhìn đoạn thẳng BC dưới một góc vuông đều nằm trên đường tròn đường kính BC.
 · Đường tròn (C) bán kính r có: 
 Chu vi: C = 2pr.	Diện tích: S = pr2.
3. Diện tích xung quanh và thể tích của hình trụ:
 Hình trụ có bán kính đường tròn đáy r và chiều cao h có diện tích và thể tích được tính theo công thức:
Sxq = 2prh
V = pr2h
4. Diện tích xung quanh và thể tích hình nón:
 Hình nón có bán kính đường tròn đáy r, độ dài đường sinh l và chiều cao h có diện tích và thể tích được tính theo công thức:
Sxq = prl
V = 
5. Diện tích mặt cầu và thể tích hình cầu:
 Mặt cầu bán kính r có diện tích và thể tích hình cầu tương ứng được tính theo công thức:
S = 4pr2
V = pr3
 6. Diện tích toàn phần:
	· Diện tích toàn phần của một hình đa diện là tổng diện tích của tất cả các mặt đa diện đó.
	· Diện tích toàn phần của hình trụ là tổng diện tích xung quanh và diện tích hai đáy.
	· Diện tích toàn phần của hình nón là tổng diện tích xung quanh và diện tích mặt đáy.
 Ví dụ: Trong không gian cho tam giác vuông OIM vuông tại I, góc IOM bằng 300 và cạnh IM = a. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay.
	a) Tính diện tích xung quanh của hình nón tròn xoay đó.
	b) Tính thể tích khối nón tròn xoay được tạo bởi hình nón tròn xoay nói trên.
 Ví duï: Trong khoâng gian, cho hình vuoâng ABCD caïnh a. Goïi I vaø H laàn löôït laø trung ñieåm cuûa caùc caïnh AB vaø CD. Khi quay hình vuoâng ñoù xung quanh truïc IH ta ñöôïc moät hình truï troøn xoay.
	a) Tính dieän tích xung quanh cuûa hình truï troøn xoay ñoù.
	b) Tính theå tích cuûa khoái truï troøn xoay ñöôïc giôùi haïn bôûi hình truï noùi treân.
BÀI TẬP RÈN LUYỆN
Bài 1: Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi:
 a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư.
 b) Ba cạnh của một tam giác cân khi quanh quanh trục đối xứng của nó.
 c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông.
 d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh.
Bài 2: Cho một hình nón có đường cao bằng 12cm, bán kính đáy bằng 16cm. Tính diện tích xung quanh của hình nón đó.
Bài 3: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc SAB bằng 600. Tính diện tích xung quanh và thể tích của hình nón đỉnh S, đáy là đường tròn ngoại tiếp tứ giác ABCD.
Bài 4: Một mặt phẳng đi qua trục của một khối trụ cắt khối trụ đó theo một hình vuông cạnh a. Tính theo a diện tích xung quanh và thể tích của khối trụ đó.
Bài 5: Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh 2a. Tính diện tích xung quanh và thể tích của hình nón đó.
Bài 6: Một khối trụ có chiều cao bằng 12 và bán kính đáy bằng 5. Một mặt phẳng song song với trục và cách trục một khoảng là 3 cắt khối trụ theo thiết diện là hình gì? Cho biết diện tích của thiết diện đó.
Bài 7: Cho khối nón có chiều cao là 12, bán kính đáy là 5. Một mặt phẳng đi qua đỉnh của khối nón và hai đường sinh cắt đáy theo dây cung có độ dài là 13. Cho biết độ dài các cạnh và diện tích thiết diện tạo thành.
Bài 8: Một hình trụ có bán kính đáy r = 5cm và có khoảng cách giữa hai đáy bằng 7cm.
 a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên.
 b) Cắt khối trụ bởi mặt phẳng song song với trục và cách trục 3cm. Hãy tính diện tích của thiết diện được tạo nên.
Bài 9: Một hình trụ có bán kính r và chiều cao h = r.
 a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
 b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.
 c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. Tính khoảng cách giữa đường thẳng AB và trục của hình trụ.
Bài 10: Cho hình nón tròn xoay có đường cao h = 20cm, bán kính đáy r = 25cm.
 a) Tính diện tích xung quanh của hình nón đã cho.
 b) Tính thể tích của khối nón được tạo thành bởi hình nón đó.
 c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Tính diện tích của thiết diện đó.
Bài 11: Một hình trụ có hai đáy là hai hình tròn (O; r) và (O'; r). Khoảng cách giữa hai đáy là OO' = . Một hình nón đỉnh là O' và có đáy là hình tròn (O; r).
 a) Gọi S1 là diện tích xung quanh của hình trụ và S2 là diện tích xung quanh của hình nón, hãy tính tỉ số giữa S1 và S2.
 b) Mặt xung quanh của hình nón chia khối trụ thành hai phần, hãy tính tỉ số thể tích hai phần đó.
Bài 12: Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng a.
 a) Tính diện tích xung quanh, diện tích đáy và thể tích của khối nón tương ứng.
 b) Cho dây cung BC của đường tròn đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng chứa đáy một góc 600. Tính diện tích tam giác SBC.
Bài 13: Một hình trụ có bán kính r và có chiều cao cũng bằng r. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC và AD không phải là đường sinh của hình trụ. Tính diện tích của hình vuông đó và côsin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy.
Bài 14: Cho một mặt phẳng (P) và đường thẳng d đi qua một điểm cố định và tạo với (P) một góc a không đổi (với 00 < a < 900). Chứng minh rằng d luôn thuộc mặt nón cố định.
Bài 15: Cho mặt phẳng (P) và một đường tròn tâm O trên đó. Điểm M di động trên (O). Đường thẳng d đi qua M và vuông góc với mp(P). Chứng minh rằng đường thẳng d luôn thuộc một mặt trụ cố định.
Bài 16: Trong không gian cho hai điểm A, B cố định và có độ dài AB = 20cm. Gọi d là một đường thẳng thay đổi luôn luôn đi qua A và cách B một khoảng bằng 10cm. Chứng tỏ rằng đường thẳng d luôn luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó.
Bài 17: Cho đường tròn tâm O bán kính r nằm trên mp(P). Từ những điểm M thuộc đường tròn này ta kẻ những đường thẳng vuông góc với (P). Chứng minh rằng những đường thẳng như vậy nằm trên một mặt trụ tròn xoay. Hãy xác định trục và bán kính của mặt trụ đó.
§2. MẶT CẦU
I- MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN ĐẾN MẶT CẦU:
 1. Mặt cầu:
 Tập hợp những điểm M trong không gian cách điểm O cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm O bán kính r.
	· Mặt cầu tâm O, bán kính r được kí hiệu: S(O; r) hay viết tắt là (S).
	· Ta có:
S(O; r) = {M ï OM = r}
Hình biểu diễn của mặt cầu
 · Nếu hai điểm CD nằm trên mặt cầu S(O; r) thì đoạn thẳng CD được gọi là dây cung của mặt cầu đó.
 · Dây cung AB đi qua tâm O được gọi là một đường kính của mặt cầu. Khi đó độ dài đường kính bằng 2r.
 2. Điểm nằm trong và nằm ngoài mặt cầu:
 Cho mặt cầu S(O; r) và một điểm A bất kì trong không gian.
· Nếu OA = r thì ta nói điểm A nằm trên mặt cầu S(O; r)
· Nếu OA < r thì ta nói điểm A nằm trong mặt cầu S(O; r)
· Nếu OA > r thì ta nói điểm A nằm ngoài mặt cầu S(O; r)
 Tập hợp các điểm thuộc mặt cầu S(O; r) cùng với các điểm nằm trong mặt cầu đó được gọi là khối cầu hoặc hình cầu tâm O bán kính r.
 3. Đường kinh tuyến và vĩ tuyến của mặt cầu:
 Ta có thể xem mặt cầu là một mặt tròn xoay tạo nên bởi nửa đường tròn quay quanh trục chứa đường kính của nửa đường tròn đó.
 · Giao tuyến của mặt cầu với nửa mặt phẳng có bờ là trục của mặt cầu được gọi là kinh tuyến.
 · Giao tuyến (nếu có) của mặt cầu với các mặt phẳng vuông góc với trục được gọi là vĩ tuyến của mặt cầu.
 · Hai giao điểm của mặt cầu với trục được gọi là hai cực của mặt cầu
II – GIAO CỦA MẶT CẦU VÀ MẶT PHẲNG:
 Cho mặt cầu (S) tâm O, bán kính r và mặt phẳng (P). Ta có:
Mặt cầu (S) và mp(P) không có điểm chung
(P)ÇS(O; r) = Æ Û d(O, (P)) > r
Mặt cầu (S) và mp(P) có 1 điểm chung
(mặt phẳng (P) tiếp xúc với mặt cầu (S))
(P) Ç S(O; r) = {H} Û d(O, (P)) = r
Khi đó: (P) gọi là tiếp diện của mặt cầu (S), H gọi tiếp điểm
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) tâm H, bán kính r'
(P) Ç S(O; r) = C(H, r') Û d(O, (P)) < r
· Taâm H laø hình chieáu cuûa O treân mp(P)
· Baùn kính r' = 
Maët phaúng (P) ñi qua taâm O cuûa maët caàu
Khi ñoù giao tuyeán cuûa mp(P) vaø S(O; r) laø ñöôøng troøn C(O; r) goïi laø ñöôøng troøn lôùn.
III – GIAO CUÛA MAËT CAÀU VÔÙI ÑÖÔØNG THAÚNG, TIEÁP TUYEÁN CUÛA MAËT CAÀU:
 Cho maët caàu (S) taâm O, baùn kính r vaø ñöôøng thaúng D. Ta coù: 
Ñöôøng thaúng D khoâng caét maët caàu (S)
D Ç S(O; r) = Æ Û d(O, D)) > r
Ñöôøng thaúng D caét maët caàu (S) taïi 2 ñieåm
D Ç S(O; r) = {M; N} Û d(O, D)) < r
Đường thẳng D tiếp xúc mặt cầu (S) tại H
Khi đó: D gọi là tiếp tuyến của mặt cầu (S), H gọi là tiếp điểm.
 * Nhận xét:
 Qua một điểm A nằm trên mặt cầu S(O; r) có vô số tiếp tuyến của mặt cầu. Tất cả các tiếp tuyến này đều vuông góc với bán kính OA của mặt cầu tại A và đều nằm trên tiếp diện của mặt cầu tại A.
 Qua một điểm A nằm ngoài mặt cầu S(O; r) có vô số tiếp tuyến với mặt cầu. Các tiếp tuyến này tạo thành mặt nón đỉnh A. Khi đó độ dài các đoạn thẳng kẻ từ A đến các tiếp điểm đều bằng nhau.
 * Mặt cầu nội tiếp, ngoại tiếp hình đa diện:
 Mặt cầu nội tiếp hình đa diện nếu mặt cầu đó tiếp xúc với tất cả các mặt của hình đa diện. Còn nói hình đa diện ngoại tiếp mặt cầu.
 Mặt cầu ngoại tiếp hình đa diện nếu tất cả các đỉnh của hình đa diện đều nằm trên mặt cầu. Còn nói hình đa diện nội tiếp mặt cầu.
Mặt cầu tâm O bán kính r ngoại tiếp hình chóp S.ABCD
khi và chỉ khi OA = OB = OC = OD = OS = r
 Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc mặt đáy. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC biết AB = BC = a và SA = .
 Ví duï 2: Cho hình choùp ñeàu S.ABCD coù caïnh ñaùy baèng a, goùc SAC baèng 600. Xaùc ñònh taâm vaø tính baùn kính maët caàu ñi qua caùc ñænh cuûa hình choùp.
 Ví duï 3: Cho töù dieän OABC coù OA, OB, OC vuoâng goùc nhau töøng ñoâi moät, OA = OB = OC = a. Xaùc ñònh taâm vaø baùn kính maët caàu ngoaïi tieáp töù dieän OABC.
IV- COÂNG THÖÙC TÍNH DIEÄN TÍCH MAËT CAÀU VAØ THEÅ TÍCH KHOÁI CAÀU:
 Cho maët caàu (S) coù baùn kính r, ta coù:
	· Dieän tích maët caàu: S = 4pr2
	· Theå tích khoái caàu: V = pr3
 * Chuù yù:
	· Dieän tích S cuûa maët caàu baùn kính r baèng boán laàn dieän tích hình troøn lôùn cuûa maët caàu ñoù.
	· Theå tích V cuûa khoái caàu baùn kính r baèng theå tích khoái choùp coù dieän tích ñaùy baèng dieän tích maët caàu vaø coù chieàu cao baèng baùn kính cuûa khoái caàu ñoù.
BÀI TẬP RÈN LUYỆN
Bài 1: Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu đi qua 6 đỉnh của hình lăng trụ.
Bài 2: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Hãy xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.
Bài 3: Cho hình chóp S.ABC có bốn đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
Bài 4: Cho hình chóp tam giác S.ABC có SA ^ (ABC), tam giác ABC vuông tại B, cạnh AC = 5a, AB = 3a và SA = a.
 a) Tính thể tích khối chóp, từ đó suy ra khoảng cách từ A đến mp(SBC).
 b) Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
Bài 5: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, BB' = b, CC' = c.
 a) Xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.
 b) Tính bán kính của đường tròn là giao tuyến của mặt phẳng (ABCD) với mặt cầu trên.
Bài 6: Từ một điểm M nằm ngoài mặt cầu S(O; r) kẻ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D.
 a) Chứng minh rằng MA.MB = MC.MD.
 b) Gọi MO = d. Tính MA.MB theo r và d.
Bài 7: Cho mặt cầu S(O; r) tiếp xúc với mp(P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M ta kẻ hai tiếp tuyến của mặt cầu cắt (P) tại A và B. Chứng minh rằng góc AMB bằng góc AIB.
BÀI TẬP RÈN LUYỆN
Bài 1: Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Biết AB = AD = a, tính diện tích xung quanh và thể tích của khối nón được tạo thành khi quay đường gấp khúc BDA quanh cạnh AB.
Bài 2: Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).
 a) Chứng minh H là tâm đường tròn ngoại tiếp tam giác BCD. Tính độ dài đoạn AH.
 b) Tính diện tích xung quanh và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác BCD và chiều cao AH.
Bài 3: Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng D vuông góc với mặt phẳng (ABCD). Trên D lấy điểm S sao cho OS = . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích của mặt cầu và thể tích của khối cầu được tạo nên bởi mặt cầu đó.
Bài 4: Cho hình trụ có bán kính đáy r, trục OO' = 2r và mặt cầu đường kính OO'.
 a) Hãy so sánh diện tích mặt cầu và diện tích xung quanh của hình trụ đó.
 b) Hãy so sánh thể tích khối trụ và thể tích khối cầu được tạo nên bởi hình trụ và mặt cầu đã cho.