Đề thi tuyển sinh lớp 10 thpt năm học 2015 - 2016 môn toán lớp 9

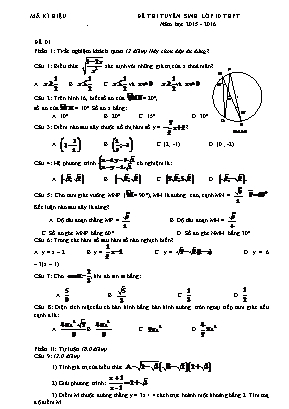
MÃ KÍ HIỆU
.
ĐỀ THI TUYỂN SINH LỚP 10 THPT
Năm học 2015 - 2016 
ĐỀ 01
Phần 1: Trắc nghiệm khách quan (2 điểm) Hãy chọn đáp án đúng?
Câu 1: Biểu thức xác định với những giá trị của x thoả mãn?
A. 	B. 	C. và 	. và 
Câu 2: Trên hình 16, biết số đo của = 20o,
số đo của = 10o. Số đo x bằng:
	A. 10o	B. 20o	 	C. 15o	D. 30o	
Câu 3: Điểm nào sau đây thuộc đồ thị hàm số y = ?	
	A. 	B. 	C. (2; -1)	D. (0 ; -2)
Câu 4: Hệ phương trình có nghiệm là:
	A. 	B. 	C. 	D. 
Câu 5: Cho tam giác vuông MNP (= 90o), MH là đường cao, cạnh MN = . Kết luận nào sau đây là đúng?
A. Độ dài đoạn thẳng MP = 	 B. Độ dài đoạn MH = 
 C. Số đo góc MNP bằng 60o	 D. Số đo góc NMH bằng 30o
Câu 6: Trong các hàm số sau hàm số nào nghịch biến?
A. y = x – 2	B. y = 	 C. y = 	D. y = 6 – 3(x – 1)
Câu 7: Cho , khi đó sin bằng: 
A. 	 	B. 	 	C. 	 D. 
Câu 8: Diện tích mặt cầu có bán kính bằng bán kính đường tròn ngoại tiếp tam giác đều cạnh a là:
	A. 	B. 	C. 	D. 
Phần II: Tự luận (8,0 điểm)
Câu 9: (2,0 điểm)
1) Tính giá trị của biểu thức 
2) Giải phương trình: .
3) Điểm M thuộc đường thẳng y = 3x + 4 cách trục hoành một khoảng bằng 2. Tìm toạ độ điểm M.
Câu 10: (2,0 điểm) 
Cho phương trình (1).
1) Giải phương trình với m = 0. 
2) Tìm hệ thức liên hệ giữa hai nghiệm của phương trình (1), độc lập với m. 
3) Tìm m để phương trình (1) có hai nghiệm x1; x2 thoả mãn .
Câu 11: (3,0 điểm) 
Cho đường tròn (O) và điểm P nằm ngoài đường tròn. Từ P vẽ hai tiếp tuyến PA, PB (A, B là hai tiếp điểm). PO cắt đường tròn (O) tại K, I (K nằm giữa P và O) và cắt AB tại H. Gọi D là điểm đối xứng của B qua O, C là giao điểm của PD và đường tròn (O).
a) Chứng minh tứ giác BHCP nội tiếp. 
b) Chứng minh .
c) Đường tròn ngoại tiếp tam giác ACH cắt IC tại M, AM cắt IB tại Q. Chứng minh rằng M là trung điểm của AQ.
Câu 12: (1,0 điểm). 
Cho ba số dương a, b, c thoả mãn a + b + c = 3. Chứng minh rằng: . Đẳng thức xảy ra khi nào?
ĐỀ 02
2. Giải phương trình: 
3. Tìm m để đường thẳng y = 2x - 3 và đường thẳng y = (m - 1)x + m - 2 cắt nhau tại một điểm trên trục tung?
Câu 2: (2,0 điểm) 
1. Giải bất phương trình: x2 - x(x+2) > 3x- 1 
2. Giải hệ phương trình: 
3. Cho phương trình bậc 2 với ẩn số : (1)
Giải phương trình (1)với m = 2
Với giá trị nào của m thì phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1< 2 < x2
Câu 3: (3,0 điểm)	
Cho đường tròn (O; R) dây AB cố định không đi qua tâm. C là điểm nằm trên cung nhỏ AB. Kẻ dây CD vuông góc với AB tại H. Kẻ CK vuông góc với đường thẳng DA.
1.Chứng minh: Bốn điểm A, H, C, K cùng thuộc một đường tròn.
2.Chứng minh: CD là tia phân giác của góc BCK.
3.KH cắt BD tại E. Chứng minh: CE BD
4.Khi C di chuyển trên cung nhỏ AB. 
 Xác định vị trí của điểm C để CK. AD + CE. DB có giá trị lớn nhất ?
Câu 4: (1,0 điểm) 
1. Tìm x, y thỏa mãn : 
2. Cho các số thực dương a, b, c , chứng minh rằng : + + 
------------------------Hết-------------------------
----------------Hết---------------
MÃ KÍ HIỆU
.
ĐÁP ÁN ĐỀ THI TUYỂN SINH LỚP 10 THPT
Năm học 2015 - 2016 
MÔN: TOÁN
 (Hướng dẫn chấm gồm 03 trang)
Phần I: Trắc nghiệm khách quan (2,0 điểm)
Câu
1
2
3
4
5
6
7
8
Đáp án
C
C
C
B
B
D
B
A
Phần II: Tự luận (8,0 điểm).
Câu
Nội dung
Điểm
Câu 9
(2,0)
1) Tính giá trị của biểu thức 
2) Giải phương trình (ĐKXĐ: )
Giải tìm ra được 
Đối chiếu với ĐKXĐ kết luận nghiệm
3) Điểm M thuộc đường thẳng y = 3x + 4 cách trục hoành một khoảng bằng 2. Tìm toạ độ điểm M.
Điểm M cách trục hoành một khoảng bằng 2 nên tung độ của M có thể bằng 2 hoặc -2.
Với y = 2 thì 2 = 3x +4 Þ toạ độ của điểm M(; 2).
Với y = -2 thì -2 = 3x +4 Suy ra toạ độ của điểm M(; 2).
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Câu 10
(2,0)
1) Giải phương trình với m = 0:
Với m = 0 thì phương trình (1) trở thành x2 – 1 = 0 
Kết luận được nghiệm của phương trình.
2) Tìm hệ thức liên hệ giữa hai nghiệm của phương trình (1), độc lập với m:
Ta có nên phương trình (1) có 2 nghiệm phân biệt x1; x2 với mọi m.
Áp dụng hệ thức Viet ta có:
3. Tìm m để phương trình (1) có hai nghiệm x1; x2 thoả mãn :
Suy ra 7m2 = 1
Kết luận được 
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Câu 11
(3,0)
Vẽ hình đúng cho câu a
a.(0,5đ)
 Ta có: 
Suy ra tứ giác BHCP nội tiếp.
b. (1,0đ)
.Ta sẽ chứng minh . 
Thật vậy:
 (Tứ giác HCPB nội tiếp). (1)
 . (2)	
Mà (3).
Từ (1), (2), (3) ta có đfcm.
c. (1,25đ)
Vì H là trung điểm của AB nên ta
sẽ chứng minh .
Có: 
Suy ra 
HM//BQ.
Kết luận được M là trung điểm của AQ
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Câu 12
(1,0)
Cho ba số dương a, b, c thoả mãn a + b + c =3. Chứng minh rằng
. Đẳng thức xảy ra khi nào?
Đặt 
Suy ra 
Dấu bằng xảy ra khi và chỉ khi a = b = c = 1
0,25
0,25
0,25
0,25
 Hết -----
PHẦN KÝ XÁC NHẬN
ĐỀ THI TUYỂN SINH LỚP 10 THPT 
MÔN: TOÁN
MÃ ĐỀ THI: 
TỔNG SỐ TRANG (ĐỀ THI VÀ HƯỚNG DẪN CHẤM) LÀ: 05 TRANG