Đề thi thử thpt quốc gia năm 2015 - Môn: Toán thời gian: 180 phút, không kể thời gian phát đề

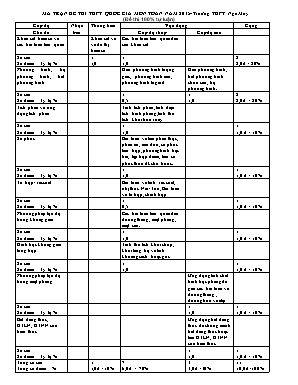
 MA TRẬN ĐỀ THI THPT QUỐC GIA MÔN TOÁN NĂM 2015- Trường THPT Ngô Mây
(Đề thi 100% tự luận)
Cấp độ
Nhận biết
Thông hiểu
Vận dụng
Cộng
Chủ đề
Cấp độ thấp
Cấp độ cao
Khảo sát hàm số và các bài toán liên quan 
Khảo sát và vẽ đồ thị hàm số
Các bài toán liên quan đến câu khảo sát
Số câu:
Số điểm: Tỷ lệ %
1
1,0
1
1,0
2
2,0đ = 20%
Phương trình, hệ phương trình, bất phương trình
Giải phương trình lượng giác, phương trình mũ, phương trình lôgarit
Giải phương trình, bất phương trình chứa căn, hệ phương trình. 
Số câu:
Số điểm: Tỷ lệ %
1
0,5
1
1,0
2
2,0đ = 20%
Tích phân và ứng dụng tích phân
Tính tích phân, tính diện tích hình phẳng, tính thể tích khối tròn xoay
Số câu:
Số điểm: Tỷ lệ %
1
1,0
1
1,0 đ = 10%
Số phức
Bài toán về tìm phần thực, phần ảo, mô đun, số phức liên hợp, phương trình bậc hai, tập hợp điểm, tìm số phức thỏa đk cho trước.
Số câu:
Số điểm: Tỷ lệ %
1
1,0
1
1,0 đ = 10%
Tổ hợp-xác suất
Bài toán về tính xác suất, nhị thức Niu-Tơn, Bài toán về tổ hợp, chỉnh hợp
Số câu:
Số điểm: Tỷ lệ %
1
0,5
1
1,0 đ = 10%
Phương pháp tọa độ trong không gian
Các bài toán liên quan đến đường thẳng, mặt phẳng, mặt cầu.
Số câu:
Số điểm: Tỷ lệ %
1
1,0
1
1,0 đ = 10%
Hình học không gian tổng hợp
Tính thể tích khối chóp, khối lăng trụ và tính khoảng cách hoặc góc
Số câu:
Số điểm: Tỷ lệ %
1
1,0
1
1,0 đ = 10%
Phương pháp tọa độ trong mặt phẳng
Ứng dụng tính chất hình học phẳng để giải các bài toán về đường thẳng , đường tròn và elip
Số câu:
Số điểm: Tỷ lệ %
1
1,0
1
1,0 đ = 10%
Bất đẳng thức, GTLN, GTNN của biểu thức
Ứng dụng bất đẳng thức để chứng minh bất đẳng thức hoặc tìm GTLN, GTNN của biểu thức
Số câu:
Số điểm: Tỷ lệ %
1
1,0
1
1,0 đ = 10%
Tổng số câu:
Tổng số điểm: %
1
1,0đ =10%
7
6,0đ = 70%
3
3,0đ =30% 
11
10,0đ=100%
SỞ GD & ĐT HÀ NỘI
Trường THPT VẠN XUÂN -LB ĐỀ THI THỬ THPT QUỐC GIA NĂM 2015
 ----- MÔN: TOÁN
 Thời gian: 180 phút, không kể thời gian phát đề
Câu 1: (2 điểm) 
Cho hàm số 
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
2. Viết phương trình tiếp tuyến của (C) tại M có hoành độ 
Câu 2 (1 điểm) 
1. Giải phương trình 
2. Tìm số phức biết rằng: 
Câu 3 (0,5 điểm)
 Giải bất phương trình 
Câu 4 (1điểm)
Giải hệ phương trình 
Câu 5 (1điể Tính tích phân 
Câu 6 (1 điểm) Cho hình chóp S.ABC có AB = AC = a. BC = . , . Tính thể tích khối chóp S.ABC.
Câu 7 (1 điểm) 
Trong mặt phẳng với hệ trục toạ độ Oxy cho cho hai đường thẳng . d2: 3x +6y – 7 = 0. Lập phương trình đường thẳng đi qua điểm P( 2; -1) sao cho đường thẳng đó cắt hai đường thẳng d1 và d2 tạo ra một tam giác cân có đỉnh là giao điểm của hai đường thẳng d1, d2.
Câu 8 (1 điểm) 
 Trong không gian với hệ trục toạ độ Oxyz cho 4 điểm A( 1; -1; 2), B( 1; 3; 2), C( 4; 3; 2), D( 4; -1; 2) và mặt phẳng (P) có phương trình:. Gọi A’là hình chiêú của A lên mặt phẳng Oxy. Gọi ( S) là mặt cầu đi qua 4 điểm A’, B, C, D. Xác định toạ độ tâm và bán kính của đường tròn (C) là giao của (P) và (S). 
Câu 9 (0,5 điểm) 
Tìm số nguyên dương n biết: Câu 10 (1 điểm) Cho a, b, c là ba số dương thoả mãn : a + b + c = . Tìm giá trị nhỏ nhất của biểu thức 
-------------- Hết--------------SƯU TẦM LÊ QUANG CHIẾN
Đáp án
Câu
Nội dung
Điểm
1. 1
 Khảo sát hàm số và vẽ đồ thị hàm số ..................
1,00
1) Hàm số có TXĐ: 
0,25
2) Sự biến thiên của hàm số:
a) Giới hạn vô cực và các đường tiệm cận:
* 
Do đó đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số 
* đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số 
0,25
b) Bảng biến thiên:
Ta có: 
Bảng biến thiên:
x
- ¥ 2 + ¥
y’
-
-
y
2
-¥
+ ¥
2
* Hàm số nghịch biến trên mỗi khoảng và 
0,25
3) Đồ thị:
+ Đồ thị cắt trục tung tại và cắt trục hoành tại điểm 
O
y
x
2
3/2
3/2
2
+ Nhận xét: Đồ thị nhận giao điểm I( 2; 2) của hai tiệm cận làm tâm đối xứng.
0,25
1. 2
Viết phương trình tiếp tuyến của (C) tại M có hoành độ 
1,00
Ta có: , 
Phương trình tiếp tuyến với ( C) tại M có dạng: 
0,5x2
2. 1
 Giải phương trình lượng giác ......
0,5 điểm
0,25
0,25
2. 2
Tìm số phức biết rằng: 
0,5 điểm
Giả sử: (với )
Ta có 
0,25
Từ (2) ta suy ra 
x = y +7 (3) thay vào (1) ta được : 
Với y = - 4 . Vậy z = 3 – 4i
0,25
3. 
Giải bất phương trình.........................
0,5 điểm
ĐK: 
Với điều kiện (*) bất phương trình tương đương với: 
0,25
Kết hợp với điều kiện (*) ta có: hoặc x < 0.
0,25
4.
Giải hệ phương trình
1 điểm
Phương trình (2) 
0,25
* Với x = 0 thay vào (1) 
0,25
* Với thay y = 1 – 3x vào (1) ta được: 
Đặt Vì nên 
0,25
Vậy hệ phương trình đã cho có nghiệm và
0,25
5.
Tính tích phân.............................
1 điểm
+) Tính . Đặt 
Đổi cận: 
0,25
0,25
+) Tính . Đặt 
0,25
0,25
0,25
6
Tính thể tích hình chóp .........................
1 điểm
S
A
B
C
M
N
Theo định lí côsin ta có: 
Suy ra . Tương tự ta cũng có SC = a. 
0,25
Gọi M là trung điểm của SA , do hai tam giác SAB và SAC là hai tam giác cân nên MB ^ SA, MC ^ SA. Suy ra SA ^ (MBC).
Ta có 
0,25
Hai tam giác SAB và SAC có ba cặp cạnh tương ứng bằng nhau nên chúng bằng nhau. Do đó MB = MC hay tam giác MBC cân tại M. Gọi N là trung điểm của BC suy ra MN ^ BC. Tương tự ta cũng có MN ^ SA. 
. 
0,25
Do đó 
0,25
7
Lập phương trình đường thẳng
1 điểm
d1 có vectơ chỉ phương ; d2 có vectơ chỉ phương 
Ta có: nên và d1 cắt d2 tại một điểm I khác P. Gọi d là đường thẳng đi qua P( 2; -1) có phương trình: 
0,25
d cắt d1, d2 tạo ra một tam giác cân có đỉnh I khi và chỉ khi d tạo với d1 ( hoặc d2) một góc 450
0,25
* Nếu A = 3B ta có đường thẳng 
0,25
* Nếu B = -3A ta có đường thẳng 
Vậy qua P có hai đường thẳng thoả mãn yêu cầu bài toán. 
0,25
8
Xác định tâm và bán kính của đường tròn........
1 điểm
Dễ thấy A’ ( 1; -1; 0)
* Giả sử phương trình mặt cầu ( S) đi qua A’, B, C, D là: 
0,25
Vì nên ta có hệ: 
Vậy mặt cầu ( S) có phương trình: 
0,25
(S) có tâm , bán kính 
+) Gọi H là hình chiếu của I lên (P). H là tâm của đường tròn ( C)
+) Gọi ( d) là đường thẳng đi qua I và vuông góc với (P). 
(d) có vectơ chỉ phương là: 
Suy ra phương trình của d:
Do nên: 
0,25
 , (C) có bán kính 
0,25
9
Tìm số nguyên dương n biết.......
0,5 điểm
* Xét (1) 
* Lấy đạo hàm cả hai vế của (1) ta có: (2) 
 Lại lấy đạo hàm cả hai vế của (2) ta có: 
0,25
 Thay x = 2 vào đẳng thức trên ta có: 
0,25
10
Tìm giá trị nhỏ nhất của biểu thức
1 điểm
áp dụng Bất đẳng thức Côsi cho ba số dương ta có 
 (*)
áp dụng (*) ta có 
0,25
áp dụng Bất đẳng thức Côsi cho ba số dương ta có 
0,25
Suy ra 
Do đó 
0,25
Dấu = xảy ra 
Vậy P đạt giá trị nhỏ nhất bằng 3 khi 
0,25