Đề thi kiểm tra học kỳ II môn toán lớp 12 năm học 2015 - 2016 thời gian làm bài 90 phút (không kể thời gian giao đề)

 SỞ GD-ĐT HÀ NỘI CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM
Trường THPT Hoài đức A Độc lập – Tự do – Hạnh phúc
 -----&œ----- -----—µ–-----
ĐỀ THI KIỂM TRA HỌC KỲ II MÔN TOÁN LỚP 12 NĂM HỌC 2015-2016
Thời gian làm bài 90 phút (Không kể thời gian giao đề)
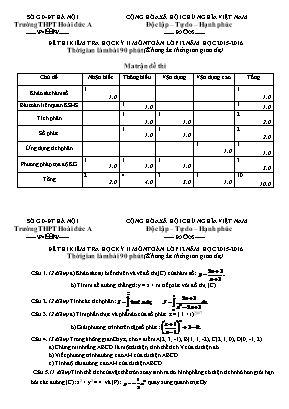
Ma trận đề thi
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
Tổng
Khảo sát hàm số
1
1,0
1
1,0
Bài toán liên quan KSHS
1
1,0
1
1,0
Tích phân
1
1,0
1
1,0
2
2,0
Số phức
1
1,0
1
1,0
2
2,0
Ứng dụng tích phân
1
1,0
1
1,0
Phương pháp tọa độ KG
1
1,0
1
1,0
1
1,0
3
3,0
Tổng
2
2.0
4
4,0
3
3,0
1
1,0
10
10,0
 SỞ GD-ĐT HÀ NỘI CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM
Trường THPT Hoài đức A Độc lập – Tự do – Hạnh phúc
 -----&œ----- -----—µ–-----
ĐỀ THI KIỂM TRA HỌC KỲ II MÔN TOÁN LỚP 12 NĂM HỌC 2015-2016
Thời gian làm bài 90 phút (Không kể thời gian giao đề)
Câu 1. (2 điểm) a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: 
	 	 b) Tìm m để đường thẳng d: y = x + m tiếp xúc với đồ thị (C)
Câu 2. (2 điểm) Tính các tích phân: 
Câu 3. (2 điểm) a) Tìm phần thực và phần ảo của số phức z = ( 1 + i)2017.
	 b) Giải phương trình trên tập số phức: 
Câu 4. (3 điểm) Trong không gian Oxyz, cho 4 điểm A(2; 3; -1), B(1; 1; -2), C(2; 1; 0), D(0; -1; 2).
	a) Chứng minh rằng ABCD là một tứ diện, tính thể tích V của tứ diện đó.
	b) Viết phương trình đường cao AH của tứ diện ABCD.
	c) Tính độ dài đường cao AH của tứ diện ABCD.
.Câu 5. (1 điểm) Tính thể tích của vật thể tròn xoay sinh ra do hình phẳng có diện tích nhỏ hơn giới hạn 
bởi các đường (C): x2 + y2 = 4 và (P): quay xung quanh trục Oy.
ĐÁP ÁN – THANG ĐIỂM
Câu
Ý
Nội dung
Điểm
1
(2đ)
a)
(1,5đ)
* TXĐ: D = R\{-1}
* Sự biến thiên: - Chiều biến thiên: 
Hàm số đồng biến trên từng khoản 
0,25
- Tiệm cận: y = 2 là tiệm cận ngang
 x = - 1 là tiệm cận đứng.
0,25
- Bảng biến thiên :
 x - ∞ -1 + ∞ 
 y’ + + 
 + ∞ 2 
 y 
 2 - ∞ 
0,25
* Đồ thị: (C) cắt Oy tại điểm (-1/2 ; 0), (C) cắt Ox tại điểm (0; 1).
Đồ thị (C) nhận giao điểm I(-1; 2) của hai đường tiệm cận làm tâm đối xứng.
 y
 I 2
 1
 x
 -1 O
0,25
b)
(0,5đ)
d tiếp xúc với đồ thị (C) khi và chỉ khi hệ phương trình sau có nghiệm: 
0,75
Vậy m = 0 hoặc m = 5 thỏa yêu cầu đề bài.
0,25
2
(2đ)
I
(1đ)
0,50
0,50
J
(1đ)
0,50
2ln 
0,50
3
(2đ)
a)
(1đ)
(1 + i)2017 = [(1 + i)2]1008(1 + i) = (2i)1008(1 + i) = 21008(1 + i) = 21008 + i21008.
0,75
Vậy Phần thực của z là 21008, phần ảo của z là 21008
0,25
b)
(1đ)
0,75
. Vậy pt có nghiệm 
0,25
4
(3đ)
a)
(1đ)
Ta có: 
0,25
0,25
 là ba véc tơ chung gốc, không đồng phẳng nên ABCD là tứ diện
0,25
0,25
b)
(1đ)
Mặt phẳng (BCD) có 1 VTPT là 
0,50
AH (BCD) nên đường cao AH đi qua A(2; 3; -1) và có 1 VTCP là 
0,25
Đường cao AH có pt tham số: 
0,25
c)
(1đ)
0,50
0,50
5
(1đ)
Coi đường tròn (C) : x2 + y2 = 4 là hợp của đồ thị của hai hàm số và . 
Hình phẳng có diện tích nhỏ hơn giới hạn bởi các đường (C2) và (P)
0,25
Xét hệ phương trình: 
Các đường (C2) và (P) cắt Oy tại các điểm có tung dộ lần lượt là y = – 2 và y = 0
0,25
Thể tích khối tròn xoay cần tính là: 
0,25
0,25
Chú ý: 
- Điểm bài thi làm tròn tới 0,5 điểm.
- Thí sinh làm theo cách khác nhưng đúng thì vẫn cho điểm tương ứng đến phần đó.
- Trong quá trình chấm, nếu thầy cô gặp những vấn đề khó xử lý thì thông tin kịp thời cho nhóm chấm để cùng nhau bàn bạc, giải quyết.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác SAB là tam giác đều và 
mp(SAB) vuông góc với mp(ABCD). Gọi M, N, P, Q lần lượt là trung điểm của BC, CD, DS, SB.
	a) Chứng minh rằng mp(ANP) vuông góc với đáy ABCD.
	b) Tính khoảng cách giữa hai đường thẳng MQ và AP.
	c) Tính thể tích của khối tứ diện SANP.
Giải:
Gọi O là trung điểm của AB. đều nên SO . Do đó SO (ABCD). 
Chọn hệ trục tọa độ Oxyz như hình vẽ. 
Khi đó: , , , ,, , , 
 z 
 S 
 P 
 Q 
 A D 
 O N y 
 B M C 
 x