Đề thi khảo sát chất lượng khối 12 lần 3 môn: Toán năm học 2015 - 2016 thời gian làm bài 180 phút, không kể thời gian giao đề

 TRƯỜNG THPT VIỆT TRÌ
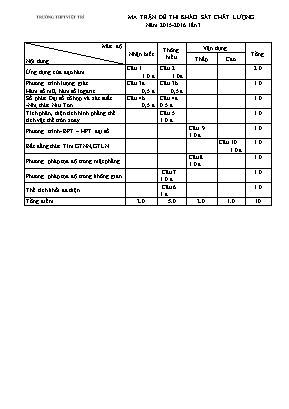
MA TRẬN ĐỀ THI KHẢO SÁT CHẤT LƯỢNG 
Năm 2015-2016 lần 3
Mức độ
Nội dung
Nhận biết
Thông hiểu
Vận dụng
Tổng
Thấp
Cao
Ứng dụng của đạo hàm
Câu 1.
1.0 đ
Câu 2.
 1.0đ
2.0
Phương trình lượng giác
Hàm số mũ, hàm số logarit
Câu 3a
0,5 đ
Câu 3b
0,5 đ
1.0 
Số phức Đại số tổ hợp và xác suất
-Nhị thức Niu Tơn
Câu 4b
0,5 đ 
Câu 4a
0.5 đ
1.0
Tích phân, diện tích hình phẳng thể tích vật thể tròn xoay 
Câu 5
1.0 đ
1.0
Phương trình- BPT – HPT đại số
Câu .9
1.0 đ
1.0
Bất đẳng thức.Tìm GTNN,GTLN 
Câu 10
1.0 đ
1.0
Phương pháp tọa độ trong mặt phẳng
Câu 8
1.0 đ
1.0
Phương pháp tọa độ trong không gian
 Câu 7
1.0 đ
1.0
Thể tích khối đa diện
 Câu 6
1 đ
1.0
Tổng điểm
2.0
5.0
2.0
1.0
10
 TRƯỜNG THPT VIỆT TRÌ
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG KHỐI 12 LẦN 3 Môn: Toán 
Năm học 2015-2016 
Thời gian làm bài 180 phút, không kể thời gian giao đề
Câu 1 (1.0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số .
Câu 2 (1.0 điểm). Trong tất cả các hình chữ nhật có chu vi là 60 cm. Tìm hình chữ nhật có diện tích lớn nhất.
Câu 3 (1.0 điểm). 
a) Cho . Tính giá trị biểu thức: .
b) Giải phương trình sau : 
Câu 4 (1.0 điểm). 	
a) Cho số phức z thỏa mãn: . Tìm mô đun của số phức .
b) Đội văn nghệ nhà trường gồm có 6 học sinh khối 10, 5 học sinh khối 11 và 4 học sinh khối 12. chọn ngẫu nhiên 7 học sinh từ đội văn nghệ kể trên để biểu diễn văn nghệ trong lễ bế giảng. Tính xác suất để trong đội văn nghệ không có học sinh khối 12. 
Câu 5 (1.0 điểm). Tính tích phân: .
 Câu 6 (1.0 điểm). Cho hình lăng trụ đứng , có đáy là tam giác vuông, , góc giữa hai mặt phẳng và mặt phẳng bằng .Tính thể tích của khối lăng trụ và khoảng cách giữa hai đường thẳng chéo nhau .
Câu 7 (1.0 điểm). Trong không gian với hệ trục tọa độ Oxyz. Cho đường thẳng , mặt phẳng . Xác định tọa độ giao điểm của đường thẳng (d) với mặt phẳng (P). Viết phương trình mặt cầu tâm I(d) tiếp xúc với mặt phẳng (P) và có bán kính bằng .
Câu 8 (1.0 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC nội tiếp trong đường tròn tâm I, có đỉnh A thuộc đường thẳng d: x + y - 2 = 0, D(2; -1) là chân đường cao của tam giác ABC hạ từ đỉnh A. Gọi điểm E(3; 1) là chân đường vuông góc hạ từ B xuống đoạn AI; điểm 
P(6;-1) thuộc đường thẳng AC. Tìm tọa độ các đỉnh của tam giác ABC.
 Câu 9 (1,0 điểm) Giải hệ phương trình sau trên tập số thực : 
Câu 10 (1.0 điểm). Tìm m để mọi số thực x ta có :
-----------------Hết-----------------
Thí sinh không được dùng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:SBD:...........
TRƯỜNG THPT VIỆT TRÌ
ĐÁP ÁN ĐỀ THI THỬ THPT QUỐC GIA 2015-2016- LẦN 3
 Môn: Toán 
Câu
Nội dung
Điểm
Câu 1 (1.0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số . 
1.0
*TXĐ: D=R
 *Sự biến thiên:
0.25
Bảng biến thiên : 
0.25
x
y'
y
- 
+ 
- 1
1
0
0
+
-
+
-
+ 
4
0
0.25
*Đồ Thị: Cắt trục Ox tại 2 điểm (1;0); (-2;0); cắt trục Oy tại điểm (0;-2). Đi qua điểm (2; -4) 
0.25
2
Câu 2 (1.0 điểm). Trong tất cả các hình cn có chu vi là 60 cm. Tìm hình chữ nhật có diện tích lớn nhất.
Gọi một cạnh của hình chữ nhật là x (cm) (0< x<30 ) .khi đó cạnh còn lại là (30-x )(cm)
Theo bài ra thì diện tích của hình chữ nhật là : 
Vậy diện tích S của hcn lớn nhất = 225 khi x =15 (cm)
( Chú ý : Bài này có nhiều cách giải )
0,25
 0,25
0,25
0,25
3 
Câu 3 (1.0 điểm). 
a) Cho . Tính giá trị biểu thức: 
ta có 
0.25
0.25
 b) Giải phương trình sau : 
 Pt . Nhận xét x=1 là nghiệm của phương trình .cm x=1 là nghiệm duy nhất của phương trình : 
Vậy pt đã cho có duy nhất một nghiệm x=1
0.25
0.25
4
 Câu 4 (1.0 điểm). 	
a) Cho số phức z thỏa mãn: . Tìm mô đun của số phức 
0.5
0.25
 Thay vào tính được Tính được 
0.25
 b) Đội văn nghệ nhà trường gồm có 6 học sinh khối 10, 5 học sinh khối 11 và 4 học sinh khối 12. chọn ngẫu nhiên 7 học sinh từ đội văn nghệ kể trên để biểu diễn văn nghệ trong lễ bế giảng. Tính xác suất để trong đội văn nghệ không có học sinh lớp 12. 
0.5
 Chọn 7 em không gian mẫu của phép thử là : 
Gọi A là biến cố chọn 7 em không có em nào lớp 12 
0.25
 Xác suất cần tính là 
0.25
5
 Câu 5 (1.0 điểm). Tính tích phân: .
1 đ
 Ta có 
0.25
0.25
 =
0.25
0.25
6
 Câu 6 (1.0 điểm). Cho hình lăng trụ đứng, có đáy là tam giác vuông, , góc giữa hai mặt phẳng và mặt phẳng bằng .Tính thể tích của khối lăng trụ và khoảng cách giữa hai đường thẳng chéo nhau .
1.0
 Gọi M là trung điểm của BC 
Ta có 
Tam giác ABC vuông cân nên 
Tam giác AMA’ vuông tại A nên AA’=AM.tan(AA’M)=
B
A’
A
C
M
C’
B’
M’
H’
0.25
0.25
 Gọi M’ là trung điểm của B’C’ dẽ cm được hai mp (A’BM’) //(MAC’)
Suy ra d(A’B, A’C) =d((A’BM’) ,(MAC’))=d(C’;(A’M’B))=d(B’;(A’M’B))
Gọi B’H là đ/cao của tam giác BB’M’ .Ta chứng minh được B’H chính là khoảng cách cần tính 
Áp dụng hệ thức lượng trong tam giác vuông MBB’ ta có 
0.25
0.25
7
 Câu 7 (1.0 điểm). Trong không gian với hệ trục tọa độ Oxyz. Cho đường thẳng , mặt phẳng . Xác định tọa độ giao điểm của đường thẳng (d) với mặt phẳng (P). Viết phương trình mặt cầu tâm I(d) tiếp xúc với mặt phẳng (P) và có bán kính bằng . 
1.0
 Tọa độ giao điểm là nghiệm của hệ phương trình 
0.25
0.25
 Gọi I(1+2t;3+t; -3-3t) thuộc d; theo bài ra ta có 
0.25
 Với 
0.25
8
 Câu 8 (1.0 điểm). Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC nội tiếp trong đường tròn tâm I, có đỉnh A thuộc đường thẳng d: x + y - 2 = 0, D(2; -1) là chân đường cao của tam giác ABC hạ từ đỉnh A. Gọi điểm E(3; 1) là chân đường vuông góc hạ từ B xuống AI; điểm P(6;-1) thuộc đường thẳng AC. Tìm tọa độ các đỉnh của tam giác ABC.
1.0
Gọi M là điểm đối xứng của A qua I. 
Ta có (Do tứ giác ABDE nội tiếp). Từ đó suy ra mà . 
Ta có .
Phương trình AC : . Ta có . Tọa độ của A thỏa hệ phương trình .
Ta có , .
Phương trình BE : .o
0.25
0.25
 Phương trình BD : .
Tọa độ của B thỏa hệ phương trình .
Ta có , nên Tọa độ của C thỏa hệ phương trình . 
Kết luận : , , . 
0.25
0.25
9
 Giải hệ phương trình: .
1.0
0.25
+) ĐKXĐ: (*)
+) 
Vì 
Thế vào (2) được: 
+) +) 
 (4)
+) Xét hàm số với có 
 nên đồng biến trên .
+) Mà pt(4) có dạng: 
Do đó (T/M)
+) Với 
Vậy hệ đã cho có tập nghiệm là: 
0.25
0.25
0.25 
 10
Câu 10 (1.0 điểm). Tìm m để mọi số thực x ta có :
HD: Nếu thì Vt = Vp (phương trình không có nghiệm).
Nếu thì ta xét tam giác vuông ABC với , AB = 4; AC = 3. 
Gọi AD là phân giác của góc A, lấy M thuộc tia AD. 
Đặt AM = x, xét và xét .
Từ đó suy ra Vt = . Vậy theo yêu cầu bài toán thì 
Dấu đẳng thức xảy ra khi ,hay
Vậy dấu “=” xảy ra khi .
Dự phòng nhé 
{ Cho các số thực dương . Tìm giá trị nhỏ nhất của biểu thức sau:
Áp dụng bất đẳng thức Côsi ta có
.
Đẳng thức xảy ra khi và chỉ khi .
0.25
0.25
0.25
0.25
 Suy ra 
Đặt . Khi đó ta có: 
0.25
 Xét hàm số với ta có .
0.25
Bảng biến thiên
 +
Do đó ta có khi và chỉ khi 
0.25
Vậy ta có , đẳng thức xảy ra khi và chỉ khi .
Vậy giá trị nhỏ nhất của P là khi và chỉ khi .