Đề thi khảo sát chất lượng khối 12 lần 2 môn: Toán năm học 2015 - 2016 thời gian làm bài 180 phút, không kể thời gian giao đề

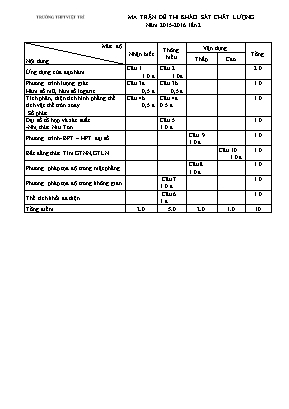
 TRƯỜNG THPT VIỆT TRÌ
MA TRẬN ĐỀ THI KHẢO SÁT CHẤT LƯỢNG 
Năm 2015-2016 lần 2
Mức độ
Nội dung
Nhận biết
Thông hiểu
Vận dụng
Tổng
Thấp
Cao
Ứng dụng của đạo hàm
Câu 1.
1.0 đ
Câu 2.
 1.0đ
2.0
Phương trình lượng giác
Hàm số mũ, hàm số logarit
Câu 3a
0,5 đ
Câu 3b
0,5 đ
1.0 
Tích phân, diện tích hình phẳng thể tích vật thể tròn xoay 
 Số phức 
Câu 4b
0,5 đ 
Câu 4a
0.5 đ
1.0
Đại số tổ hợp và xác suất
-Nhị thức Niu Tơn 
Câu 5
1.0 đ
1.0
Phương trình- BPT – HPT đại số
Câu .9
1.0 đ
1.0
Bất đẳng thức.Tìm GTNN,GTLN 
Câu 10
1.0 đ
1.0
Phương pháp tọa độ trong mặt phẳng
Câu 8
1.0 đ
1.0
Phương pháp tọa độ trong không gian
 Câu 7
1.0 đ
1.0
Thể tích khối đa diện
 Câu 6
1 đ
1.0
Tổng điểm
2.0
5.0
2.0
1.0
10
 TRƯỜNG THPT VIỆT TRÌ
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG KHỐI 12 LẦN 2 Môn: Toán 
Năm học 2015-2016 
Thời gian làm bài 180 phút, không kể thời gian giao đề
Câu 1 (2.0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số .
Câu 2 (1.0 điểm). Cho hàm số có đồ thị .Viết phương trình tiếp tuyến của tại điểm có hoành độ .
Câu 3 (1.0 điểm). 
a) Giải phương trình sau :
b) Giải phương trình sau : 
Câu 4 (1.0 điểm). 
a) Tính tích phân: . 
b) Trên mặt phẳng phức tìm tập hợp điểm biểu diễn số phức z thoả mãn: .
Câu 5 (1.0 điểm). Trường trung học phổ thông Việt Trì có 30 lớp trong đó có 10 lớp 10, 
10 lớp 11và 10 lớp 12, mỗi chi đoàn (lớp) có một em làm bí thư. Ban chấp hành Đoàn trường muốn chọn 5 em bí thư đi thi cán bộ đoàn giỏi. Tìm xác suất để 5 em được chọn 
có đủ cả ba khối lớp.
 Câu 6 (1.0 điểm). Cho hình chóp có , tam giác cân tại , , . Tính thể tích của khối chóp , xác định tâm và tính diện tích mặt cầu ngoại tiếp hình chóp .
Câu 7 (1.0 điểm). Trong không gian với hệ trục tọa độ Oxyz. Viết phương trình mặt phẳng (P) đi qua điểm cắt các tia Ox, Oy và Oz lần lượt tại sao cho .
Câu 8 (1.0 điểm). Trong mặt phẳng với hệ tọa độ . Cho hình vuông ABCD, M là trung điểm của đoạn N thuộc đoạn sao cho . Đường tròn tâm N qua M cắt AC tại , đường thẳng đi qua có phương trình :. Tìm tọa độ điểm B.
Câu 9 (1.0 điểm). Giải hệ phương trình : 
 trên tập số thực .
Câu 10 (1.0 điểm). Cho là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức 
.
-----------------Hết-----------------
Thí sinh không được dùng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:SBD:...........
TRƯỜNG THPT VIỆT TRÌ
ĐÁP ÁN ĐỀ THI THỬ THPT QUỐC GIA 2015-2016- LẦN 2 
 Môn: Toán 
Câu
Nội dung
Điểm
1
Câu 1 (2.0 điểm). Cho hàm số (1).
a)Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
1.0
TXĐ D= R
0.25
 y’= Hàm số không có cực trị 
Hàm số luôn đồng biến trên khoảng 
Giới hạn tại vô cực: 
0.25
BBT x
y’
y
-
+
0.25
Đồ thị
0.25
2
 Câu 2 ( 1.0 điểm).Cho hàm số có đồ thị . Viết phương trình tiếp tuyến của tại điểm có hoành độ .
 Ta có 
Với và 	
Khi đó tọa độ tiếp điểm là 	
Vậy phương trình tiếp tuyến của là: y= 9(x-1)+2020 hay y= 9x+2011	
(0,25)
 0,25)
(0,25)
(0,25)
3 
 Câu 3 (1.0 điểm). 
 a)Giải phương trình sau :
pt 
0.25
0.25
b) Giải phương trình sau : 
Pt tương đương với 
0.25
0.25
4
Câu 4 (1.0 điểm). a) Tính tích phân: . 
0.5
 Đặt ta có 
Suy ra: 
0.25
0.25
b)Trên mặt phẳng phức tìm tập hợp điểm biểu diễn số phức z thoả mãn: 
0.5
Gọi số phức z = x+yi () điểm biểu diễn M(x;y) trên mặt phẳng phức
0.25
Vậy tập hợp các điểm bd số phức z là đường tròn tâm I(1;0) bán kính R =1
0.25
5
 Câu 5 (1.0 điểm). Trường trung học phổ thông Việt Trì có 30 lớp trong đó có 10 lớp 10, 10 lớp 11và 10 lớp 12, mỗi chi đoàn (lớp) có một em làm bí thư. Bch Đoàn trường muốn chọn 5 em bí thư đi thi cán bộ đoàn giỏi. Tìm xác suất để 5 em được chọn có đủ cả ba khối lớp
 Chọn 5 em không gian mẫu của phép thử là : 
0.5
 Gọi A là biến cố chọn 5 em bí thứ có đủ các khối lớp 
0.25
Xác suất cần tính là 
0.25
6
 Câu 6 (1.0 điểm). Cho hình chóp
 có , tam giác cân tại ,.Tìm tâm diện tích mặt cầu ngoại tiếp hình chóp .
1.0
sinC= 
sinA=sin2C = 2sinC.cosC = 
theo định lý sin trong tam giác ABC ta có 
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ta có IA=R .Dựng ngoại tiếp tam giác ABC. Mặt phẳng trung trực SA cắt trục đường tròn tại J khi đó J chính là tâm mặt cầu ngoại tiếp SABC 
0.25
0.25
0.25
 Gọi r là bán kính mặt cầu ngoại tiếp SABC khi đó 
Diện tích mặt cầu cần tính là B
S
A
M
C
J
N
I
0.25
7
 Câu 7 (1.0 điểm).
 Trong không gian với hệ trục tọa độ Oxyz. Viết phương trình mặt phẳng (P) đi qua điểm cắt các tia Ox, Oy và Oz lần lượt tại sao cho .
1.0
Gọi mặt phẳng cần tìm có dạng 
0.25
 Vì mp(P) đi qua điểm M nên ta có phương trình 
0.25
0.25
 Mặt phẳng cần tìm là : 6x+ 3y +2z - 25 =0 
0.25
8
 Câu 8 (1.0 điểm).
 Trong mặt phẳng với hệ tọa độ . Cho hình vuông ABCD , M là trung điểm của sao cho ,đường tròn tâm N qua M cắt AC tại , đường thẳng đi qua có phương trình :.Tìm tọa độ điểm B.
1.0
 MN cắt đường tròn tâm N tại K .ta chứng mính được tứ giác MIJK nội tiếp
gócNKJ = gócAIM =450 ===> góc JNK= 900 
NJ vuông góc với (MN) nên có phương trình : x-y-2 =0 ===>(
Tam giác JMN vuông cân nên 
 K
A
C
B
D
N
M
J
I
P
0.25
0.25
Với M(-2;1) gọi ta có 
 tìm được A(-3;4) , vì A là trung điểm của IP nên I(1; 2)
Ta có B(3;6) 
Tương tự Với M(3;-4) t tìm được A(6;-5) , I(4; -1) và B(8;1) 
 Vậy tọa độ điểm B(3;6) hoặc B(8;1) 
0.25
0.25
9
 Câu 9 (1.0 điểm). 
 Giải hệ phương trình : 
1.0
 Phương trình (2) tương đương với 
0.25
Thay vào phương trình ta được: 
 hoặc . Khi đó ta được nghiệm là và .
0.25
0.25
0.25 
Câu 10 (1.0 điểm). 
 Cho là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức 
.
Ta có 
0.25
 và 
0.25
 Suy ra , Đặt 
0.25
 xét .
t
0 4 + 
f’
 - 0 +
f
 -
Suy ra giá trị nhỏ nhất của P bằng - khi .
Cách 2: 
0.25