Đề tham khảo tuyển sinh vào lớp 10 (2016 - 2017)

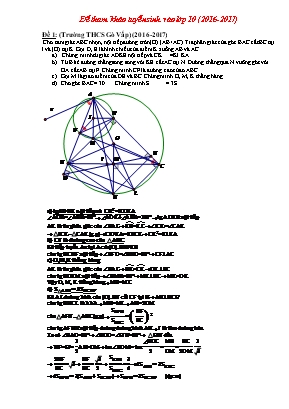
Đề tham khảo tuyển sinh vào lớp 10 (2016-2017)
Đề 1: (Trường THCS Gò Vấp) (2016-2017)
 Cho tam giác ABC nhọn, nội tiếp đường tròn (O) (AB<AC).Tia phân giác của góc BAC cắt BC tại I và (O) tại K. Gọi D, E là hình chiếu của điểm K xuống AB và AC.
 Chứng minh tứ giác ADKE nội tiếp và CK =KI.KA.
Từ B kẻ đường thẳng song song với KE cắt AC tại N. Đường thẳng qua N vuông góc với OA cắt AB tại F. Chứng minh CF là đường cao của DABC.
Gọi M là giao điểm của DE và BC.Chứng minh O, M, K thẳng hàng.
Cho góc BAC= 30 . Chứng minh S = 3S .
Đề 2:(Trường THCS Nguyễn Văn Nghi) (2016-2017)
Cho △ABC nhọn nội tiếp (O;R) có 2 đường cao BE, CF.Tiếp tuyến tại B và C của (O) cắt nhau tại S.Gọi M là giao điểm của BC và OS.
Chứng minh tứ giác SBOC nội tiếp và O(M.OS=R)
Chứng minh AF.BC=EF.AC
Chứng minh góc AME = góc ASB
AM cắt EF tại N,AS cắt BC tại P.Chứng minh NP⊥BC
Đề 3: (Trường THCS Phan Tây Hồ) (2016-2017)
Cho DABC nhọn (AB<AC).Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E.BE và CF cắt nhau tại H.AH cắt BC tại I và cắt (O) tại M(M ở giữa A và H).
Chứng minh các tứ giác AEHF, ICAF nội tiếp.
Chứng minh EB là tia phân giác của góc FEI và góc EFO= góc FIO
BE cắt đường tròn đường kính AC tại Q(E nằm giữa B và Q).Chứng minh DCMQ cân.
Giả sử BC cố định , A di động sao cho DABC nhọn,Tìm điều kiện DABC để (EC+ EB) đạt giá trị lớn nhất
Đề 4: (Trường THCS Phạm Văn Chiêu) (2016-2017)
Cho đường tròn (O) đường kính AB.Trên (O) lấy C sao cho AC>BC.Tiếp tuyến tại B và C của (O) cắt nhau tại N.ON cắt BC tại H.
Chứng minh tứ giác OBNC nội tiếp và ON//AC
Từ O kẻ đường thẳng vuông góc với AC tại K,cắt đường thẳng NC tại M.Chứng minh MA là tiếp tuyến của (O) và AB tiếp xúc với đường tròn đường kính MN.
AN cắt (O) tại E.Chứng minh HC là phân giác của góc AHE.
MB cắt AN tại I.Chứng minh K, I, H thẳng hàng
Đề 5: (Trường THCS Trường Sơn) (2016-2017)
Cho △ABC (AB<AC) nội tiếp (O;R) có 3 đường cao AD, BE, CF cắt nhau tại H.
Chứng minh tứ giác BFEC nội tiếp và △AEF∼△ABC
Chứng minh DA là phân giác của góc EDF
EF cắt (O) tại M và N(F nằm giữa M và E).Chứng minh AM là tiếp tuyến của đường tròn ngoại tiếp △MHD
Đường tròn đường kính AH cắt (O) tại K,AK cắt BC tại I.Chứng minh I, E, F thẳng hàng.
Đề 6: (Trường THCS Nguyễn Du) (2016-2017)
Cho(O;R) và (O';r) giao nhau tại A và B(O, O' ở 2 phía AB và R>r).Gọi C là điểm tùy ý trên tia đối AB.Vẽ tiếp tuyến CD và CE với (O;R)(D và E là tiếp điểm, E thuộc cung nhỏ AB) và vẽ tiếp tuyến CF với (O';r)(F là tiếp điểm và thuộc cung lớn AB).
Chứng tỏ tứ giác ODCE nội tiếp và OC⊥DE.
Chứng tỏ CD = CF
Đường thăng DA cắt (O';r) tại M và đường thảng AE cắt (O';r) tại N.Đường thẳng DE cắt MN tại I.Chứng tỏ góc ABE= góc MBI
Chứng tỏ khi C di động trên tia đối tia AB thì DE luôn đi qua một điểm cố định. 
Đề 7: (3,5 điểm) (Trường THCS Nguyễn Trãi)(2016-2017)
Qua điểm A nằm ngoài đường tròn (O).Từ A vẽ 2 tiếp tuyến AB và AC(B và C là 2 tiếp điểm) và vẽ cát tuyến ADE của (O) sao cho tâm O nằm trong góc EAC.
Chứng minh OA⊥BC tại H và AB.AC=AD.AE
Chứng minh OHDE nội tiếp.
Gọi K là giao điểm của DE và BC.Chứng minh : AD.KE=AE.KD
Gọi M là điểm đối xứng của B qua E.AM cắt BC tại N.Chứng minh: ND//BM
Đề 8 : (Trường THCS An Nhơn) (2016-2017)
Từ điểm S cố định ở bên ngoài đường tròn (O) cho trước, vẽ 2 tiếp tuyến SA, SB (A và B là 2 tiếp điểm), kẻ dây cung BN // SA và M là giao điểm thứ 2 của SN với (O).
Chứng minh SA.SB=SM.SN
Gọi K là trung điểm của MN.Chứng minh KS là phân giác của góc AKB.
Từ M kẻ đường thẳng song song với SA cắt AB và AN lần lượt tại I và E.Chứng minh I là trung điểm của ME.
Chứng minh SA, NI và BM đồng quy.
Đề 9: (Trường THCS Quang Trung) (2016-2017)
Cho DABC nhọn (AB<AC).Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và F.BF và CE gặp nhau tại H.
Chứng minh AH ^ BC tãi D và tứ giác AEHF nội tiếp.
Tiếp tuyến tại F của đường tròn (O) qua trung điềm I của AH.
Gọi M là giao điểm của EF và BC.Chứng minh OE là tiếp tuến chung của đường tròn ngoại tiếp DAEF và đường tròn ngoại tiếp DMED.
Chứng minh MH ^ AO
Đề 10:(Trường THCS Huỳnh Văn Nghệ) (2016-2017)
Cho đường tròn (O;R) và điểm E ngoài đường tròn sao cho OE=3R.Đường thẳng OE cắt (O) tại A và B(A nằm giữaE và B).Tiếp tuyến EM của (O) gặp 2 tiếp tuyến Ax và By của (O) lần lượt tại C và D.
Chứng minh AC+BD=CD và góc COD=90°
Kẻ đường kính MN của (O),EN cắt (O) tại F.Vẽ MH⊥AB tại H.Chứng minh các tứ giác EMHF và FHON nội tiếp.
Gọi I là giao điểm của AD và BC.Chứng minh I là trung điểm của MH
Gọi K là giao điểm của AN và BF.Chứng minh AK.AN+BK.BF=4R 
Đề 11: (Trường THCSThông Tây Hội) (2016-2017)
Cho đường tròn (O) có tâm O, đường kính BC. Lấy một điểm A trên đường tròn (O) sao cho AB > AC. Từ A, vẽ AH vuông góc với BC (H thuộc BC). Từ H, vẽ HE vuông góc với AB và HF vuông góc với AC (E thuộc AB, F thuộc AC). 
Chứng minh rằng AEHF là hình chữ nhật và OA vuông góc với EF.
Đường thẳng EF cắt đường tròn (O) tại P và Q (E nằm giữa P và F).
Chứng minh AP2 = AE.AB. Suy ra APH là tam giác cân
Gọi D là giao điểm của PQ và BC; K là giao điểm cùa AD và đường tròn (O) (K khác A). Chứng minh AEFK là một tứ giác nội tiếp.
Gọi I là giao điểm của KF và BC. Chứng minh IH2 = IC.ID
Đề 12:(Trường THCS Lý Tự Trọng)(2016-2017)
Cho điểm A ngoài đường tròn(O),kẻ cát tuyến ABC với (O).Các tiếp tuyếntại B và C của (O) cắt nhau tại D.Qua D kẻ đường thẳng vuông góc với OA tại H và cắt (O) tại E, F(E nằm giữa D và F).Gọi M là giao điểm của OD và BC.
Chứng minh tứ giác EMOF nội tiếp
Chứng minh AE, AF là 2 tiếp tuyến của (O).
Từ B vẽ đường thẳng vuông góc với OF cắt CF tại P và EF tại Q.Chứng minh Q là trung điểm của BP.
 DF cắt BC tại I.Chứng minh MI.MA=BC/4
Đề 13:(Trường THCS Nguyễn Văn Trổi) (2016-2017)
Cho△ABC có 3 góc nhọn nội tiếp (O;R).Tiếp tuyến tại B và C của (O) cắt nhau tại T.Đường thẳng AT cắt (O) tại điểm thứ 2 là D (D khác A).Đoạn thẳng OT cắt BC tại H và cắt (O) tại G.
Chứng minh OT⊥BC và HB.HC=HO.HT
Chứng minh ∠AOH=180°-∠ADH
Từ D kẻ đường thẳng vuông góc với OB,đường thẳng này cắt BC tại M và cắt AB tại N.Chứng minh M là trung điểm của DN.
AG cắt BC tại E.Chứng minh EB.DC=EC.DB
Đề 14: (Trường THCS HERMANN GMEINER) (2016-2017)
Cho đường tròn (O) đường kính AB.Gọi Ax,By lần lượt là các tiếp tuyến tại A và B của (O).Qua điểm M thuộc (O), kẻ tiếp tuyến với (O)(M là tiếp điểm,M khác A và B).Tiếp tuyến này cắt Ax, By lần lượt tại C và D(AC>BD) và cắt AB tại Q.
Chứng minh các tứ giác OACM, OBDM nội tiếp.
OC cắt AM tại E, OD cắt BM tại F,tứ giác OEMF là hình gì? Chứng minh DM.CQ=CM.DQ
Gọi I, K lần lượt là trung điểm của OC và OD.C/m tứ giác OIMK nội tiếp.
Gọi N là giao điểm của AD và BC.Tia MN cắt AB tại H.Chứng minh MN//AC và N là trung điểm của MH.