Đề tham khảo kiểm tra 45 phút chương IV hình học 9

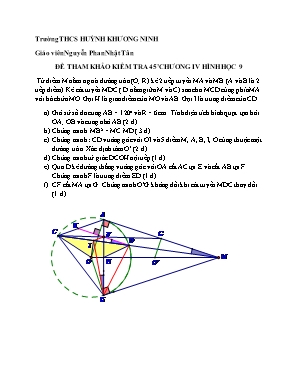
Trường THCS HUỲNH KHƯƠNG NINH
Giáo viên Nguyễn Phan Nhật Tân
ĐỀ THAM KHẢO KIỂM TRA 45’ CHƯƠNG IV HÌNH HỌC 9
 Từ điểm M nằm ngoài đường tròn (O; R) kẻ 2 tiếp tuyến MA và MB (A và B là 2 tiếp điểm). Kẻ cát tuyến MDC ( D nằm giữa M và C) sao cho MCD cùng phía MA với bờ chứa MO. Gọi H là giao điểm của MO và AB. Gọi I là trung điểm của CD.
Giả sử số đo cung AB = 1200 và R = 6cm. Tính diện tích hình quạt tạo bởi OA; OB và cung nhỏ AB (2 đ)
Chứng minh MB2 = MC.MD ( 3 đ)
Chứng minh : CD vuông góc với OI và 5 điểm M, A, B, I, O cùng thuộc một đường tròn. Xác định tâm O’ (2 đ)
Chứng minh tứ giác DCOH nội tiếp (1 đ) 
Qua D kẻ đường thẳng vuông góc với OA cắt AC tại E và cắt AB tại F. Chứng minh F là trung điểm ED (1 đ)
CF cắt MA tại G. Chứng minh O’G không đổi khi cát tuyến MDC thay đổi. (1 đ)
Gợi ý bài giải :
e) Ta có ED // MA ( cùng vuông góc OA)
Suy ra góc IFD = góc IMA ( đồng vị )
Mà góc IMA = góc IBF ( tứ giác IAMB nội tiếp)
Suy ra góc IDF = góc IBF. Vậy tứ giác IFDB nội tiếp
Suy ra góc FID = góc FBD
Mà góc ACD = góc FBD
Suy ra AC // IF, lại có I là trung điểm CD. Suy ra F là trung điểm của ED.
f) Sử dụng hệ quả Thales lần lượt trong tam giác CAG và tam giác CGM. Chứng minh G là trung điểm của AM. 
Suy ra GO’ là đường trung bình của tam giác AOM. Suy ra GO’ = ½ OA = R/2. Vậy OG’ không đổi khi cát tuyến MCD thay đổi