Đề ôn thi môn Toán Lớp 12 - Chương 4: Số phức - Chủ đề 4, Vấn đề 3: Mođun nhỏ nhất, lớn nhất có tập hợp điểm biểu diễn là một đường thẳng hoặc một elip

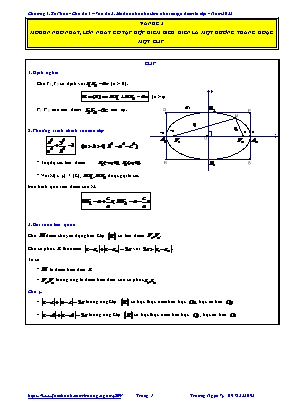
VẤN ĐỀ 3
MOĐUN NHỎ NHẤT, LỚN NHẤT CÓ TẬP HỢP ĐIỂM BIỂU DIỄN LÀ MỘT ĐƯỜNG THẲNG HOẶC MỘT ELIP 
ELIP
1. Định nghĩa
-a
a
(E)
c
-c
y
x
R
S
P
Q
O
M
	Cho F1, F2 cố định với (c > 0).
	 (a > c)
	F1, F2: các tiêu điểm, : tiêu cự.
2. Phương trình chính tắc của elip
	· Toạ độ các tiêu điểm:	.
	· Với M(x; y) Î (E), được gọi là các
bán kính qua tiêu điểm của M. 
3. Bài toán liên quan
Cho điểm chuyển động trên Elip có tiêu điểm .
Cho số phức thỏa mãn với .
Ta có: 
	· là điểm biểu diễn 
 	· tương ứng là điểm biểu diễn của số phức
Chú ý: 
	· tương ứng Elip có trục thực nằm trên trục , trục ảo trên 
	· tương ứng Elip có trục thực nằm trên trục , trục ảo trên 
DẠNG 1
SỐ PHỨC CÓ TẬP HỢP ĐIỂM BIỂU DIỄN LÀ MỘT ELIP CÓ TÂM TRÙNG GỐC TỌA ĐỘ
Cho số phức thỏa mãn . Gọi , lần lượt giá trị lớn nhất và nhỏ nhất Khi đó bằng
	A.	B.	C.	D.
Hướng dẫn giải
Cách 1: Phương pháp hình học
Gọi , . 
Theo giả thiết, ta có .
Gọi , và .
 nên tập hợp các điểm là đường elip có hai tiêu điểm và . Và độ dài trục lớn bằng .
Ta có ; và .
Do đó, phương trình chính tắc của là có các đỉnh 	
Vậy và (là các đỉnh của elip )
Vậy .
Cách 2 : Phương pháp Đại số: Bunhiacopxki
Gọi với .
Ta có .
Do đó .
Mà .
Áp dụng bất đẳng thức Bunhiacopxki, ta có
.
Do đó . Vậy .
Cho số phức thỏa mãn . Giá trị lớn nhất và nhỏ nhất của lần lượt là:
	A. 10 và 4.	B. 5 và 4.	C. 4 và 3.	D. 5 và 3.
Hướng dẫn giải
Cách 1.
Giả sử .
Ta có .
Áp dụng bất đẳng thức Bunhiacopxki, ta có 
. Chọn D. 
Cách 2. Giả sử .
Từ giả thiết, ta có .	 
Trong mặt phẳng với hệ tọa độ , gọi và , thì có dạng . Vậy tợp hợp điểm biểu diễn số phức là một Elip có độ dài trục lớn , tiêu cự . Suy ra độ dài trục bé .
Khi đó ta luôn có hay .
Cho số phức thỏa mãn . Gọi lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của . Tính .
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Gọi và là điểm biểu diễn của số phức trong mặt phẳng phức. Xét các điểm . Ta có : 
Do Tập hợp điểm là một có dạng 
.
Cho số phức thỏa mãn . Gọi , lần lượt là điểm biểu diễn số phức có môđun lớn nhất và nhỏ nhất. Gọi là trung điểm của , biểu diễn số phức , tổng nhận giá trị nào sau đây? 
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Cách 1: Phương pháp hình học
Gọi , . 
Theo giả thiết, ta có .
Gọi , và .
Khi đó nên tập hợp các điểm là đường elip có hai tiêu điểm và . Và độ dài trục lớn bằng .
Ta có ; và .
Do đó, phương trình chính tắc của là .	
Vậy khi có điểm biểu diễn là .
và khi có điểm biểu diễn là .
Tọa độ trung điểm của là .
Vậy .
Đáp án B 
Cách 2 : Phương pháp Đại số: Bunhiacopxki
Gọi với .
Ta có .
Do đó khi có điểm biểu diễn là .
Mà .
Áp dụng bất đẳng thức Bunhiacopxki, ta có
.
Do đó khi có điểm biểu diễn là .
Tọa độ trung điểm của là .
Vậy .
Trong các số phức thỏa mãn , hai số phức và có môđun nhỏ nhất. Hỏi tích là bao nhiêu
	A.	B.	C.	D.
Hướng dẫn giải
Gọi số phức thỏa mãn 
Vậy tập hợp các điểm biểu diễn số phức là đường Elip có 2 đỉnh thuộc trục nhỏ là 
Với mỗi điểm biểu diễn số phức sẽ thuộc đường tròn tâm bán kính . Vì elip và đường tròn có cùng tâm nên để nhỏ nhất thì là đỉnh thuộc trục nhỏ 
 , 
Tổng hợp 
 Đáp số chính xác là D
DẠNG 2
SỐ PHỨC CÓ TẬP HỢP ĐIỂM BIỂU DIỄN LÀ MỘT ĐOẠN THẲNG
Xét số phức thỏa mãn . Gọi , lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của . Tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Cách 1: Phương pháp hình học
Gọi là điểm biểu diễn của .
Các điểm , , . 
Ta có , mà 
Suy ra thuộc đoạn thẳng .
Phương trình đường thẳng , với .
.
.
Vậy .
Cách 2: Phương pháp hàm số
Gọi là điểm biểu diễn của . Các điểm , , .
Ta có , mà .
Suy ra thuộc đoạn thẳng .
Phương trình đường thẳng , với .
Ta có 
Đặt , .
,( nhận ) 
Ta có , , .
Vậy , .
,..
Xét các số phức thoả mãn . Tìm giá trị lớn nhất của 
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi lần lượt là điểm biểu diễn của các số phức .
Ta có: và .
 thuộc đoạn .
Gọi là điểm biểu diễn của số phức .
 hoặc .
Ta có : và . Vậy .
Xét các số phức thoả mãn điều kiện : . Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi lần lượt là điểm biểu diễn của các số phức .
Ta có: và .
 thuộc đoạn .
Gọi là điểm biểu diễn của số phức .
Do đó mà .
 là hình chiếu vuông góc của lên đoạn 
Tọa độ điểm là nghiệm của hệ phương trình thuộc đoạn . Vậy .
Xét các số phức thỏa mãn Gọi lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của . Tính 
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi và là điểm biểu diễn của số phức 
Gọi , suy ra 
Từ giả thiết, ta có suy ra nằm trên đoạn thẳng có phương trình 
Suy ra với 
Ta có 
.
Khảo sát hàm trên đoạn , ta được .
Suy ra 
Chọn B. 
Xét số phức thỏa mãn Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức .
	A. 	B. 
	C. 	D. 
Hướng dẫn giải
Gọi và là điểm biểu diễn của số phức 
Gọi , suy ra 
Từ giả thiết, ta có suy ra nằm trên đoạn thẳng có phương trình 
Suy ra với 
Ta có .
Khi đó .
Khảo sát hàm trên đoạn , ta được 
. Chọn B. 
Cho số phức thỏa mãn điều kiện . Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của môđun của , tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi có điểm biểu diễn trên mặt phẳng tọa độ.
Ta có 
.
Đặt thì từ (1) ta có .
 Mặt khác
Từ và suy ra thuộc đoạn thẳng .
Ta có và phương trình đường thẳng . 
Nhận xét rằng và là góc nhọn nên và Vậy . Chọn đáp án A.
Cho số phức thỏa mãn điều kiện . Gọi lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của mô đun , tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn B.
Gọi . Có điểm biểu diễn trên mặt phẳng tọa độ.
Ta có .
Điểm biểu diễn số phức trên mặt phẳng phức.
Đặt thì từ (1) ta có 
Mặt khác .
Từ suy ra thuộc đoạn thẳng. 
Ta có , .
Nhận xét góc là các góc nhọn (nhìn hình vẽ).
ta có , .
Vậy .
Xét số phức thỏa mãn Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức .
	A. 	B. 
	C. 	D. 
Hướng dẫn giải
Gọi và là điểm biểu diễn của số phức 
Gọi , suy ra 
Từ giả thiết, ta có suy ra thuộc đoạn thẳng có phương trình 
Suy ra với 
Ta có 
Khi đó 
Khảo sát hàm trên đoạn , ta được . 
Chọn A. 
Cho số phức thỏa mãn . Mệnh để nào sau đây đúng?
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn D.
Ta có .
Xét các điểm , có: .
Dấu xảy ra .
Ta có phương trình và .
Do đó .
DẠNG 3
SỐ PHỨC CÓ TẬP HỢP ĐIỂM BIỂU DIỄN LÀ MỘT ELIP CÓ TÂM KHÔNG TRÙNG GỐC TỌA ĐỘ
Cho số phức thỏa mãn . Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn D.
Ta có 
Do đó xét các điểm , ta có:
.
Dấu xảy ra , do đó và .
; .
Vậy .
	Cho số phức thỏa mãn . Tìm giá trị lớn nhất của ?
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Gọi . Ta thấy là trung điểm của .
Mà .
Do đó khi và chỉ khi: .
DẠNG 4
MỘT SỐ DẠNG KHÁC CỦA ELIP 
Cho hai số phức thỏa mãn . Giá trị nhỏ nhất của là
	A. .	B. .	C. .	D. .
Hướng dẫn giải
+ Gọi M là điểm biểu diễn số phức trong đó .
Suy ra thuộc Elip có: là các tiêu điểm, độ dài trục lớn 
Phương trình đường thẳng AB: 
+ Goị là điểm biểu diễn số phức :
.
Bài toán trở thành tìm M thuộc elip, N thuộc đường thăng để nhỏ nhất. Để nhỏ nhất thì có vị trí như hình vẽ.
Ta có: 
Suy ra: . Chọn đáp án D
Cho số phức thỏa mãn ,. Tìm giá trị lớn nhất của .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi , và lần lượt là các điểm biểu diễn cho số phức , và .
Khi đó theo đề bài ta có : và . Vì , là các điểm cố định nên quỹ tích các điểm thõa mãn các điều kiện trên là elip có độ dài trục lớn , 2 tiêu điểm là , .
Mặt khác là điểm biểu diễn cho số phức thỏa mãn là đường tròn tâm , bán kính .
Dễ thấy , , nằm trên đường thẳng .
Xét điểm nằm trong đoạn thỏa mãn .
Khi đó và tiếp xúc nhau tại .
Do đó lớn nhất khi : , lúc đó : là các đỉnh trên trục lớn , là điểm đối xứng của qua .
Xét số phức thỏa mãn . Gọi , lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Khi đó
	A. 	B. 
	C. 	D. 
Hướng dẫn giải
Chọn B
w Gọi 
w Từ giả thiết suy ra tập hợp điểm biểu diễn là đoạn thẳng . Bài toán trở thành tìm giá trị lớn nhất và giá trị nhỏ nhất của , với là một điểm bất kì trên đoạn .
w Dễ thấy cắt nên nhỏ nhất khi thẳng hàng, .
.
w Gọi là trung điểm , . Gọi là hình chiếu của lên , do nên lớn nhất khi trùng .
w Vậy .
Cho số phức z thỏa mãn . Giá trị nhỏ nhất của đạt được khi với a, b là các số thực dương. Giá trị của bằng
	A. 19.	B. 16.	C. 24.	D. 13.
Hướng dẫn giải
Chọn đáp án B.
Cách 1: Hình học
Ta có .
Gọi M, A, B, I lần lượt là điểm biểu diễn cho các số phức z, , , . 
Khi đó và .
Có I là trung điểm của đoạn thẳng AB và và .
Do I là trung điểm của đoạn thẳng AB nên
.
Áp dụng bất đẳng thức Cô-si, ta có
Kết hợp với giả thiết, suy ra .
Do đó .
Đẳng thức xảy ra khi hay MI là đường trung trực của đoạn và . Dễ dàng tìm được hoặc . Theo giả thiết thì ta lấy ứng với . Do đó và .
Cách 2: Đại số
Đặt .
Từ giả thiết, ta có 
.
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xky, ta có
.
Dấu bằng xảy ra khi và chỉ khi 
 hoặc . Theo giả thiết, ta lấy .
Cho số phức thỏa mãn . Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn D.
Ta có 
Do đó xét các điểm , ta có:
.
Dấu xảy ra , do đó và .
; .
Vậy .
Hằng ngày mình úp đề Toán ôn thi TNPT 12 trên trang trungtamgiasunhatrang.net (trong mục tài liệu môn toán) cho đến ngày 6 tháng 7 năm 2022 sẽ dừng (tầm 70 đề). Bạn đọc theo dõi tải về phục vụ học tập và giảng dạy.
Bạn đọc tải nhiều tài liệu file word toán từ lớp 8 đến 12 tại trungtamgiasunhatrang.net (trong mục tài liệu môn toán) để phục vụ giảng dạy
P/S: Tất cả tài liệu file word đều free
TÀI LIỆU CHẮC CHẮN CÓ SỰ SAI SÓT. MONG BẠN ĐỌC ĐÓNG GÓP ĐỂ HOÀN THIỆN HƠN. 
LIÊN HỆ:https://www.facebook.com/truong.ngocvy.509/