Đề ôn thi môn Toán Lớp 12 - Chương 4: Số phức - Chủ đề 4, Vấn đề 2: Mođun nhỏ nhất, lớn nhất có tập hợp điểm biểu diễn là một đường tròn, hình tròn

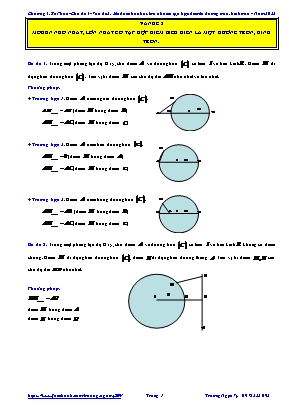
VẤN ĐỀ 2
MOĐUN NHỎ NHẤT, LỚN NHẤT CÓ TẬP HỢP ĐIỂM BIỂU DIỄN LÀ MỘT ĐƯỜNG TRÒN, HÌNH TRÒN. 
Bổ đề 1: Trong mặt phẳng tọa độ Oxy, cho điểm và đường tròn có tâm và bán kính. Điểm di động trên đường tròn . Tìm vị trí điểm sao cho độ dài nhỏ nhất và lớn nhất.
Phương pháp: 
+ Trường hợp 1: Điểm nằm ngoài đường tròn . 
 (điểm trùng điểm )
 (điểm trùng điểm )
+ Trường hợp 2: Điểm nằm trên đường tròn . 
 (điểm trùng điểm )
 (điểm trùng điểm )
+ Trường hợp 3: Điểm nằm trong đường tròn . 
 (điểm trùng điểm )
 (điểm trùng điểm )
Bổ đề 2: Trong mặt phẳng tọa độ Oxy, cho điểm và đường tròn có tâm và bán kính không có điểm chung. Điểm di động trên đường tròn , điểm di động trên đường thẳng . Tìm vị trí điểm sao cho độ dài nhỏ nhất.
Phương pháp: 
điểm trùng điểm 
điểm trùng điểm 
Bổ đề 3: Trong mặt phẳng tọa độ Oxy, cho điểm và đường tròn có tâm và bán kính. Đoạn là đường kính của đường tròn . Điểm di động trên đường tròn . Tìm vị trí điểm sao cho độ dài nhỏ nhất.
Phương pháp: 
Ta có: 
Dấu bằng xảy ra khi điểm trùng điểm 
Bổ đề 4: Trong mặt phẳng tọa độ Oxy, cho đường tròn có tâm và bán kính. Đoạn cố định nhận điểm làm trung điểm. Điểm di động trên đường tròn . Tìm vị trí điểm sao cho độ dài lớn nhất.
Phương pháp: 
Vì là đường trung tuyến nên: 
Dấu bằng xảy ra khi: 
 Hay điểm là giao điểm của đường tròn với đường tròn bán kính . 
Bổ đề 5: Trong mặt phẳng tọa độ Oxy, cho đường tròn có tâm và bán kính. Điểm cố định, nằm miền trong đường tròn . Điểm di động trên đường tròn sao cho ba điểm thẳng hàng. Tìm vị trí điểm sao cho độ dài nhỏ nhất.
Phương pháp: 
Ta có: 
Dấu bằng xảy ra khi: 
 Hay điểm là giao điểm của đường tròn với đường tròn bán kính . 
DẠNG 1
SỐ PHỨC CÓ MOĐUN NHỎ NHẤT, LỚN NHẤT
Bài toán: Cho số phức thoả mãn . Tìm GTNN, GTLN của .
Phương pháp: 
Cách 1: Phương pháp hình học
	· Đặt lần lượt là các điểm biểu diễn của các số phức . 
	· Khi đó từ giả thiết thuộc đường tròn tâm bán kính . 
	· Ta có: lớn nhất và .
	Khi đó: và .
Cách 2: Phương pháp đại số
	· Phương pháp lượng giác hoá
	· Sử dụng tính chất bất đẳng thức số phức: 
	· Sử dụng tính chất bất đẳng thức số phức: 
Cho số phức thỏa mãn Gọi lần lượt giá trị lớn nhất, giá trị nhỏ nhất của . Giá trị là: 
	A. 10.	B. 3.	C. 2.	D. 7.
Hướng dẫn giải
Phương pháp hình học
Cách 1:
Đặt số phức cần tìm là: , 
Ta có 
	· Đặt lần lượt là các điểm biểu diễn của các số phức. 
	· Khi đó từ giả thiết thuộc đường tròn tâm bán kính . 
	· Ta có: lớn nhất và .
	 Ta có 
	Khi đó: và .
Cách 2:
Đặt số phức cần tìm là: , 
Ta có 
+ là đường tròn (C) tâm , bán kính ; 
+ là đường tròn tâm O (0;0), bán kính thay đổi (C’). Khi đó số phức cần tìm phải là giao của hai đường tròn đã cho, số phức có mô đun lớn nhất là khi (C’) tiếp xúc trong với (C), nhỏ nhất khi tiếp xúc ngoài với (C). 
Vẽ hình ta thấy được:
Đáp án A
Phương pháp đại số
Cách 1: Sử dụng tính chất bất đẳng thức số phức: 
Ta có 
* 
* 
Cách 2: Sử dụng tính chất bất đẳng thức số phức: 
Ta có 
* 
Cách 3: Phương pháp lượng giác hoá
Đặt số phức cần tìm là: , 
Ta có 
+ Đặt 
khi đó 
 Với 
Mà 
Vậy 
Trong các số phức thỏa , gọi là số phức có mô đun nhỏ nhất. Khi đó
	A.Không tồn tại số phức.	B..
	C..	D..
Hướng dẫn giải
Chọn D. 
Cách 1:
Đặt . Khi đó .
Suy ra biểu diễn hình học của số phức là đường tròn tâm và bán kính .
Gọi là điểm biểu diễn số phức . Ta có: .
.
Vậy bé nhất bằng 3 khi .
Cách 2:
Đặt .
.
.
Cho số phức thỏa mãn . Giá trị nhỏ nhất của lần lượt là
	A..	B..	C..	D.
Hướng dẫn giải
Ta có 
Chọn B.
Cho số phức z thỏa mãn . Tìm giá trị lớn nhất của 
	A..	B..	C..	D.
Hướng dẫn giải
Đặt 
Ta có: . Tập hợp điểm biểu diễn số phức z là đường tròn tâm I là điểm biểu diễn số phức , tức là . Bán kính 
Vậy 
Cho số phức thỏa mãn . Giá trị lớn nhất và giá trị nhỏ nhất của lần lượt là
	A..	B..	C..	D.
Hướng dẫn giải
Ta có 
Lại có 
Chọn A.
Cho số phức thỏa mãn . Tìm môđun lớn nhất của số phức 
	A.	B.	C.	D. 
Hướng dẫn giải
Gọi . Ta có: 
Đặt .
Lúc đó: 
 đạt được khi 
Chọn D.
Cho số phức thỏa mãn . Tìm môđun lớn nhất của số phức 
	A.	B.	C.	D.
Hướng dẫn giải
Gọi .
Ta có: 
Đặt .
Lúc đó:
 đạt được khi 
Chọn B.
Cho số phức thoã mãn . Gọi và lần lượt là giá trị lớn nhất và nhỏ nhất của . Tính giá trị của biểu thức .
	A..	B..	C..	D.
Hướng dẫn giải
Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính 
Khi đó ; 
Suy ra .
Chọn A.
Cho số phức thảo mãn Tìm giá trị nhỏ nhất của 
	A. 	B.	C.	D. 
Hướng dẫn giải
Giả sử ta có: 
Đặt 
Đặt 
Dấu xảy ra khi 
Vậy 
Chọn A.
Số phức có mô đun lớn nhất và thỏa mãn điều kiện là:
	A.	B.	C.	D.
Hướng dẫn giải
+ Gọi 
Từ giả thiết ta có: 
+ Đồng thời lớn nhất. Kiểm tra các đáp án và so sánh.
Chọn D.
Cho số phức thỏa mãn . Tìm để nhỏ nhất 
	A. 	B. 	C.	D. 
Hướng dẫn giải
, là đường tròn (C) tâm I(2 ;-2), bán kính R=1(màu xanh)
 là đường tròn (C’) thay đổi(màu đỏ). GTLN là tiếp xúc ngoài tai điểm A, GTNN là tiếp xúc tại B. Trong đó A, B là giao của đường thẳng y=-x với (C). 
Ta tìm được đáp án C.
Cho số phức thỏa mãn . Tìm để nhỏ nhất 
	A. 	B. 	C. 	D. 
Hướng dẫn giải
+ Gọi số phức thỏa mãn 
Vậy tập hợp các điểm biểu diễn số phức là đường tròn có tâm bán kính 
+ Với mỗi điểm biểu diễn số phức sẽ thuộc đường tròn tâm bán kính . Vì vậy để nhỏ nhất thì đường tròn phải tiếp xúc ngoài với đường 
Khi đó điểm sẽ là tiếp điểm của đường tròn và và 
 Đáp số A
Xét các số phức thỏa mãn điều kiện . Gọi lần lượt là các số phức có môđun nhỏ nhất và môđun lớn nhất. Tính 
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Gọi .
Ta có 
Suy ra tập hợp các số phức là đường tròn có tâm , bán kính .
Phương trình đường thẳng là .
Gọi lần lượt là hai điểm biểu diễn của số phức . Khi đó tọa độ điểm là nghiệm của hệ phương trình 
 Chọn A. 
Xét các số phức thỏa mãn điều kiện . Gọi lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức Tính 
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Ta biến đổi 
Đẳng thức chứng tỏ tập các số phức là đường tròn tâm , bán kính .
Khi đó Chọn B. 
Cho số phức thỏa mãn . Gọi lần lượt giá trị lớn nhất, giá trị nhỏ nhất của . Giá trị là: 
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Phương pháp hình học
Cách 1:
Đặt số phức cần tìm là: , 
khi đó: 
	· Đặt điểm biểu diễn số phức. 
	· Khi đó từ thuộc đường tròn tâm bán kính . 
	· Ta có: lớn nhất và .
	 Ta có 
	Khi đó: và .
Cách 2:
Đặt số phức cần tìm là: , 
khi đó: 
Mà 
Ta tìm nhỏ nhất của .
+ là đường tròn (C) tâm , bán kính ; 
+ là đường tròn tâm O (0;0), bán kính thay đổi (C’). Khi đó số phức cần tìm phải là giao của hai đường tròn đã cho, số phức có mô đun lớn nhất là khi (C’) tiếp xúc ngoài với (C) nhỏ nhất khi tiếp xúc trong với (C). 
Vẽ hình ta thấy được:
Đán án D
Phương pháp đại số
Cách 1: Phương pháp lượng giác hoá
Đặt số phức cần tìm là: , 
khi đó: 
Mà 
Ta tìm nhỏ nhất của .
 Đặt , 
khi đó 
Mà 
Vậy 
Đán án D
Cách 2 : 
Đặt số phức cần tìm là: , 
khi đó: 
Mà 
Ta tìm nhỏ nhất của (2).
Thay (1) vào (2) : 
Từ (1) :.
Do đó: 
Vậy 
Đán án D
Chú ý: Các em xem thử cách nào phù hợp với kiến thức của mình nhé!!!
Cho số phức z thỏa mãn: , đặt , tìm 
	A.	B.	C.	D.
Hướng dẫn giải
Đặt số phức cần tìm là: , 
Ta có 
Mà 
Ta tìm nhỏ nhất của .
Cách 1 : Phương pháp Đại số: 
Thay (1) vào (2) : 
Từ (1) : từ đó tìm được và , do đó: 
đáp án A
Cách 2: Phương pháp hình học
+ là đường tròn (C) tâm , bán kính ; 
+ là đường tròn tâm O (0;0), bán kính thay đổi (C’). Khi đó số phức cần tìm phải là giao của hai đường tròn đã cho, số phức có mô đun lớn nhất là khi (C’) tiếp xúc ngoài với (C) nhỏ nhất khi tiếp xúc trong với (C). 
Vẽ hình ta thấy được:
từ đó tìm được và , do đó: 
đáp án A
Cách 3: Phương pháp lượng giác hoá
 Đặt , 
Khi đó 
Mà 
Vậy 
Từ đó tìm được và , do đó: 
Tìm biết là số phức thỏa mãn đạt giá trị nhỏ nhất.
	A.	B.	C.	D.
Hướng dẫn giải
Ta có: 
Nên 
Tìm GTLN của biết thỏa mãn .
	A.	B.	C.	D.
Hướng dẫn giải
Gọi . Khi đó 
Điểm biểu diễn của chạy trên đường tròn . Cần tìm M thuộc đường tròn này để OM lớn nhất. Dễ thấy OM lớn nhất khi . Vậy 
Cho số phức thỏa mãn là số thuần ảo. Khi số phức có môđun lớn nhất. Tính giá trị biểu thức .
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Ta có: là số thuần ảo
Ta có: 
 khi .
Xét số phức thỏa mãn . Hỏi giá trị lớn nhất của là:
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn A.
Ta có: 
Do đó 
Với . 
Với , sử dụng bất đẳng thức môđun ta có:
Từ suy ra .
Cho số phức thỏa điều kiện . Giá trị nhỏ nhất của bằng
	A. 2.	B. 1.	C. 3.	D. 4.
Hướng dẫn giải
Đáp án B
Giã sử .
 (1) . Suy ra .
 (2) . Suy ra ,.
Vậy giá trị nhỏ nhất của bằng .
DẠNG 2
SỐ PHỨC CÓ MOĐUN NHỎ NHẤT, LỚN NHẤT
Bài toán: Cho số phức thoả mãn . Tìm GTNN, GTLN của .
Phương pháp: 
Cách 1: Phương pháp hình học
	· Đặt lần lượt là các điểm biểu diễn của các số phức . 
	· Khi đó từ giả thiết thuộc đường tròn tâm bán kính . 
	· Ta có: lớn nhất và .
	· Khi đó: và .
Cách 2: Phương pháp đại số
Cho số phức thỏa mãn . Tìm giá trị lớn nhất của .
	A. .	B. .	C..	D. .
Hướng dẫn giải
Phương pháp hình học
	Đặt 
	· Đặt lần lượt là các điểm biểu diễn của các số phức . 
	· Khi đó từ giả thiết thuộc đường tròn tâm bán kính .
	· Ta có: lớn nhất .
	· Khi đó: 
Phương pháp đại số
Cách 1: Sử dụng tính chất bất đẳng thức số phức: 
Đặt .
Ta có 
Ta có : .
.
Cách 2: Sử dụng tính chất bất đẳng thức số phức: 
Đặt .
Ta có 
Ta có : 
.
Cho số phức thoả mãn . Tìm giá trị nhỏ nhất của biểu thức .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Ta có: Tập hợp điểm biểu diễn của số phức là đường tròn tâm bán kính .
Gọi là điểm biểu diễn của số phức . Do đó .
Cho số phức thoả mãn . Giá trị lớn nhất của là:
	A..	B. .	C. .	D. .
Hướng dẫn giải
Gọi là điểm biểu diễn của số phức trên mặt phẳng toạ độ.
Do nằm trên đường tròn tâm , bán kính .
 với .
.
Cho số phức thoả mãn . Gọi lần lượt là hai số phức làm cho biểu thức đạt giá trị nhỏ nhất và lớn nhất. Tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Ta có: Tập hợp điểm biểu diễn số phức là đường tròn tâm , bán kính .
 Gọi là điểm biểu diễn của số phức .
Phương trình đường thẳng .
Phương trình đường tròn tâm 
, .
Toạ độ là nghiệm của hệ .
Cho số phức thỏa mãn . Tìm môđun lớn nhất của số phức 
	A.	B.	C.	D.
Hướng dẫn giải
Gọi . Ta có: .
Đặt 
Chọn B.
Cho số phức thỏa mãn . Tìm môđun nhỏ nhất của số phức 
	A.	B.	C.	D.
Hướng dẫn giải
Gọi . Ta có: .
Đặt 
, khi 
Chọn C.
Cho số phức thỏa mãn: . Số phức có môđun nhỏ nhất là:
	A.	B.	C.	D..
Hướng dẫn giải
Chọn A.
Gọi , .
Ta có: 
Tập hợp các điểm trong mặt phẳng biểu diễn của số phức là đường tròn tâm và bán kính .
, với là tâm đường tròn, là điểm chạy trên đường tròn. Khoảng cách này ngắn nhất khi là giao điểm của đường thẳng nối hai điểm với đường tròn (C).
Cho số phức thỏa mãn điều kiện: và có môđun lớn nhất. Số phức có môđun bằng:
	A..	B..	C..	D..
Hướng dẫn giải
Chọn B.
Gọi 
Ta có: 
Suy ra tập hợp điểm biểu diễn số phức thuộc đường tròn tâm bán kính như hình vẽ:
Dễ thấy , 
Theo đề ta có:
là điểm biểu diễn cho sốphức thỏa mãn:
Suy ra đạt giá trị lớn nhất lớn nhất
Mà nên lớn nhất khi là đường kính đường tròn 
 là trung điểm 
Xét các số phức thỏa mãn . Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức lần lượt là:
	A. và . 	B. và . 	C. và . 	D. và .
Hướng dẫn giải
Gọi và là điểm biểu diễn số phức 
Từ giả thiết, ta có 
Khi đó tập hợp các điểm thuộc đường tròn tâm , bán kính 
Ta có . Đặt . 
Vậy Chọn B. 
Cách Đại số: Ta có . 
Theo giả thiết: 
Suy ra 
Cho số phức z thỏa mãn . Giá trị lớn nhất của là:
	A..	B.4.	C.6.	D.
Hướng dẫn giải
Ta có:
Đặt 
Tập hợp điểm biểu diễn w là đường tròn tâm I, tâm I là điểm biểu diễn của số phức , tức là , bán kính 
Vậy 
Chọn D
Cho số phức thỏa mãn . Giá trị lớn nhất của là
	A..	B..	C..	D..
Hướng dẫn giải
Gọi ta có .
Theo giả thiết nênđiểm biểu diễn cho số phức nằm trên đường tròn tâm bán kính .
Ta có .
Gọi và thì .
Do chạy trên đường tròn, cố định nên lớn nhất khi là giao của với đường tròn.
Phương trình , giao của và đường tròn ứng với thỏa mãn: nên .
Tính độ dài ta lấy kết quả .
ChọnD. 
Cho số phức thoã mãn . Gọi và lần lượt là giá trị lớn nhất và nhỏ nhất của . Giá trị của biểu thức gần bằng.
	A.6.	B.7.	C.8.	D.9
Hướng dẫn giải
Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính 
Gọi khi đó ; 
Do đó .
Chọn C.
Xét số phức thỏa mãn Tìm giá trị lớn nhất của 
	A.	B.	C.4.	D.6.
Hướng dẫn giải
Giả sử 
Ta có 
Chọn A.
Cho số phức z thỏa mãn: . Gọi A và B lần lượt là giá trị lớn nhất và nhỏ nhất của . Khi đó có giá gần nhất bằng
	A.20.	B.18.	C.64.	D.32
Hướng dẫn giải
Ta có 
Giả sử M là điểm biểu diễn số phức . Xét điểm và 
Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính 
Ta có: .
Chọn C.
Cho số phức z thỏa mãn: . Gọi A và B lần lượt là giá trị lớn nhất và nhỏ nhất của . Khi đó có giá trị bằng
	A.10.	B.-10.	C.12.	D.-12
Hướng dẫn giải
Giả sử M là điểm biểu diễn số phức . Xét điểm và 
Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính 
Ta có: .
Chọn A.
Cho số phức z thỏa mãn: . Gọi A và B lần lượt là giá trị lớn nhất và nhỏ nhất của . Khi đó có giá trị bằng
	A.20.	B.18.	C.24.	D.32
Hướng dẫn giải
Giả sử M là điểm biểu diễn số phức . Xét điểm và 
Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính 
Ta có: .
Chọn C.
Cho số phức thỏa mãn . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Giá trị của là
	A..	B..	C..	D.
Hướng dẫn giải
Đặt , khi đó 
Suy ra 
Chọn C.
Cho số phứcthỏa mãn . Giá trị lớn nhất của bằng
	A..	B..	C..	D.
Hướng dẫn giải
Ta có .
.
Đặt , khi đó 
Vậy giá trị lớn nhất là 
Chọn C.
Cho số phức thỏa mãn . Tổng giá trị lớn nhất và giá trị nhỏ nhất của bằng
	A..	B..	C..	D.
Hướng dẫn giải
Ta có .
Đặt , khi đó 
Và Vậy 
Chọn B.
Cho số phức thỏa mãn điều kiện . Giá trị lớn nhất của là
	A. .	B..	C..	D. 
Hướng dẫn giải
Đặt , khi đó 
Chọn D.
Trong tất cả các số phức thỏa mãn hãy tìm số phức có mođun nhỏ nhất.
	A..	B..	C..	D.
Hướng dẫn giải
Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính 
Ta có: .
Chọn A.
Cho số phức thoã mãn . Giá trị lớn nhất của là.
	A..	B..	C..	D.5
Hướng dẫn giải
Ta có: 
Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính 
Gọi suy ra.
Chọn D.
Gọi là số phức thỏa mãn hai điều kiện và đạt giá trị lớn nhất. Tính tích 
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Phương pháp hình học
Đặt 
Ta có 
	· Đặt lần lượt là các điểm biểu diễn của các số phức . 
	· Khi đó từ giả thiết thuộc đường tròn tâm bán kính . 
	· Ta có: lớn nhất .
	· Khi đó: viết phương trình đường thẳng là nên tọa độ là nghiệm của hệ 
 .
Để lớn nhất thì .Vậy .Suy ra 
Phương pháp đại số
Cách 1: Phương pháp lượng giác hoá
Đặt 
Ta có 
Mặt khác: 
Đặt: , với .
Dấu bằng xảy ra khi 
Cách 2 : Phương pháp Đại số: Bất đẳng thức số phức
 Đặt 
Ta có 
Mặt khác: 
 Dấu xảy ra khi và chỉ khi . 
Mà 
Cách 3 : Phương pháp Đại số: Bunhiacopxki
Đặt 
Ta có 
Mặt khác: 
Dùng bất đẳng thức Bunhiacopxki, ta có 
Lấy 
Dấu xảy ra khi và chỉ khi . Suy ra 
Chú ý: Các em xem thử cách nào phù hợp với kiến thức của mình nhé!!!
Cho số phức thỏa mãn và . Tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi .
Khi đó 
Suy ra tập hợp các điểm biểu diễn chính là đường tròn tâm 
Ta có . Dựa vào hình vẽ nhận thấy lớn nhất khi đi qua tâm. Khi đó . Suy ra 
Do đó 
Cho số phức thỏa mãn và số phức thỏa . Giá trị nhỏ nhất của là:
	A. .	B..	C..	D..
Hướng dẫn giải
Ta có: 
.
Trường hợp 1:.
Trường hợp 2: với .
.
Cho số phức. Gọi . Tính .
	A..	B..	C..	D.
Hướng dẫn giải
Ta có: .
.
Gọi 
 Tập hợp điểm biểu diễn số phức là đường tròn tâm có bán kính .
.
DẠNG 3
SỐ PHỨC CÓ MOĐUN LỚN NHẤT
Bài toán : Cho số phức thoả mãn . Tìm GTNN của biểu thức .
Phương pháp: 
	· Đặt lần lượt là điểm biểu diễn của các số phức .
	· Khi đó từ giả thiết Tập hợp điểm biểu diễn của số phức là đường tròn tâm bán kính .
	· Ta có: 
Theo BĐT bunhiacopski : 
Gọi là trung điểm của . Theo công thức đường trung tuyến ta có: 
Suy ra 
do đó .
Khi đó : 
Cho số phứcthỏa mãn điều kiện. Tính giá trị biểu thức khi đạt giá trị lớn nhất.
	A. 10	B. 2	C. 4	D. 7
Hướng dẫn giải
Chọn A
Gọi là điểm biểu diễn thỏa mãn điều kiện thì tập hợp M là đường tròn tâm , bán kính . Gọi thì .
Mà 
Nhận xét thấyluôn tạo thành 1 tam giác. Gọi là trung điểm , , theo công thức đường trung tuyến ta có 
Suy ra 
Do đó đạt giá trị lớn nhất khi lớn nhất. nằm ngoài đường tròn tâm, bán kính nên , khi đó trùng với . 
Vậy số phức thỏa mãn các yêu cầu của đề bài là.
	Cho . Gọi và là giá trị lớn nhất và nhỏ nhất của . Tính ?
	A. 	B. 	C. 	D. 
Hướng dẫn giải
. Gọi .
Gọi 
+) 
.
Dễ có . Lấy sao cho trung điểm .
Ta có Ptolemy: 
	Cho số phức thỏa mãn . Tìm giá trị lớn nhất của biểu thức .
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Gọi , ta có .
Theo bất đẳng thức Bunhiacopxky: . Chọn C. 
Cho số phức thỏa mãn điều kiện Tìm giá trị lớn nhất của biểu thức 
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Đặt .
Ta có 
Khi đó 
Đặt , khi đó với 
Xét hàm trên , ta được . Chọn B. 
Cho số phức thỏa mãn . Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Tính 
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn B
Ta có: và
.
Xét các số phức thỏa mãn . Tính khi đạt giá trị lớn nhất.
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Do . Suy ra có tâm và bán kính . Gọi , , . Suy ra 
Mặt khác ta có. Suy ra là hình chiếu vuông góc của trên thẳng hàng.Vì ta thấy nên xảy ra dấu =.
Ta có nên thẳng hàng.
Tọa độ là nghiệm của hệ
Mặt khác . Vậyđể thì Suy ra .
Cho các số phức thỏa mãn và . Giá trị lớn nhất của biểu thức bằng
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Từ giả thiết , ta có .
Khi đó: .
Suy ra điểm biểu diễn cho số phức sẽ thuộc đường tròn .
Ta có: , với .
Gọi là trung điểm của , ta có . Khi đó: .
Mặt khác: với mọi điểm , 
nên .
Vậy khi hay và .
Cho . Tìm giá trị lớn nhất của ?
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Ta có: .
Gọi . Chú ý thẳng hàng đồng thời ta có . Ta tìm max .
Ta có: 
. Theo bất đẳng thức Bunhiacopxky ta có:
. 
Chọn A.
Cho số phức thay đổi thỏa mãn . Hỏi giá trị nhỏ nhất của biểu thức là?
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn B.
Với , ta có:
.
DẠNG 4
SỐ PHỨC CÓ MOĐUN NHỎ NHẤT, LỚN NHẤT
Bài toán: Cho số phức thoả mãn . Tìm GTLN, GTNN của biểu thức .
Phương pháp: 
	· Đặt lần lượt là điểm biểu diễn của các số phức .
	· Khi đó từ giả thiết Tập hợp điểm biểu diễn của số phức là đường tròn tâm bán kính .
	· Gọi là trung điểm của . 
Theo công thức đường trung tuyến ta có: 
do đó và .
Khi đó : ; .
Cho số phức thoả mãn . Tìm giá trị lớn nhất của biểu thức .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi lần lượt là điểm biểu diễn của các số phức và .
 thuộc đường tròn tâm , bán kính .
Gọi lần lượt là điểm biểu diễn của các số phức và .
 (với là trung điểm của ).
.
Cho số phức thoả mãn . Gọi là số phức thoả mãn biểu thức đạt giá trị nhỏ nhất. Tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi lần lượt là điểm biểu diễn của các số phức và .
 thuộc đường tròn tâm , bán kính có phương trình: .
Đặt lần lượt là điểm biểu diễn của các số phức và .
 (với là trung điểm của ).
Do đó .
Phương trình đường thẳng .
Toạ độ thoả mãn hệ , do ngắn nhất nên .
DẠNG 5
SỐ PHỨC CÓ MOĐUN NHỎ NHẤT, LỚN NHẤT
Cho số phức thoả mãn . Gọi lần lượt là GTLN, GTNN của biểu thức . Tính .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Cách 1 : 
Gọi là điểm biểu diễn của số phức .
, có tâm , bán kính .
.
Do số phức thoả mãn đồng thời hai điều kiện nên và có điểm chung ; . 
Vậy .
Cách 2 : Lượng giác hóa
Đặt 
Ta có: 
Đặt 
Mà: 
có nghiệm khi: 
Vậy .
Tìm số phứcsao cho và biểu thức đạt giá trị lớn nhất.
	A. .	B..	C. .	D. . 
Hướng dẫn giải
Bunhiacopxki
Đặt 
.
 .
Dấu bằng xảy ra .
Cho số phức z thỏa mãn: , tìm để biểu thức đạt GTLN.
	A. 	B.10	C.	D. 
Hướng dẫn giải
Đặt số phức cần tìm là: , 
Khi đó: 
(Có thể Áp dụng tính chất để tính P thì ta có 
)
Ta có : 
Dấu bằng xảy ra khi: 
Giải hệ: 
Từ đó tìm được 
DẠNG 6
TẬP HỢP ĐIỂM GỒM ĐƯỜNG TRÒN VÀ ĐƯỜNG THẲNG
Bài toán: Cho hai số phức thoả mãn và , trong đó là các số phức đã biết. Tìm GTNN của .
Phương pháp: Đặt 
 thuộc đường tròn tâm bán kính .
 thuộc đường trung trực của đoạn .
Ta có: , do đó: .
Cho hai số phức thỏa mãn và Giá trị nhỏ nhất của biểu thức bằng
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Tập hợp các điểm biểu diễn số phức thỏa mãn là tập hợp các điểm
 thoả mãn phương trình: là đường tròn tâm
Tập hợp các điểm biểu diễn số phức thỏa mãn là tập hợp các điểm thỏa mãn phương trình
Khi đó là khoảng cách từ một điểm thuộc tới một điểm thuộc đường tròn 
.
Cho hai số phức thỏa mãn và . Giá trị nhỏ nhất của biểu thức bằng:
	A. .	B. .	C. 	D. 
Hướng dẫn giải
Đặt và với 
● tập hợp các số phức là đường tròn .
● 
tập hợp các số phức là đường thẳng .
Ta có đây chính là khoảng cách từ điểm đến điểm . 
Do đó Dựa vào hình vẽ ta tìm được khi . 
Cho hai số phức thỏa mãn và . Tìm giá trị nhỏ nhất của .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi là điểm biểu diễn của số phức , là điểm biểu diễn của số phức .
Ta có .
Vậy thuộc đường tròn 
Vậy thuộc đường thẳng 
Dễ thấy đường thẳng không cắt và 
Áp dụng bất đẳng thức tam giác, cho bộ ba điểm ta có.
Dấu bằng đạt tại .
Cho số phức thoả mãn và số phức thoả mãn . Tìm giá trị nhỏ nhất của biểu thức .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi là điểm biểu diễn của số phức .
Gọi là điểm biểu diễn của số phức .
 thuộc đường tròn , có tâm , bán kính .
.
Ta có: không cắt đường tròn .
Do đó . Vậy .
DẠNG 7
TẬP HỢP ĐIỂM GỒM HAI ĐƯỜNG TRÒN 
Bài toán: Cho hai số phức thoả mãn và trong đó là các số phức đã biết. Tìm GTNN, GTLN của biểu thức .
Phương pháp: Đặt .
 thuộc đường tròn tâm bán kính .
 thuộc đường tròn tâm bán kính .
Ta có: . Dựa vào các vị trí tương đối của hai đường tròn để tìm .
Cho các số phức và thỏa mãn và . Tìm giá trị nhỏ nhất của biểu thức 
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn A
Giả sử M, N lần lượt là điểm biểu diễn của số phức và 
Ta thấy hai đường tròn (I) và (J) nằm ngoài nhau. Do đó
.
đạt giá trị nhỏ nhất khi và chỉ khi .
.
Cho hai số phức thỏa mãn và . Tìm giá trị lớn nhất của .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi là điểm biều diễn số phức , là điểm biểu diễn số phức 
Số phức thỏa mãn suy ra nằm trên đường tròn tâm và bán kính .
Số phức thỏa mãn suy ra nằm trên đường tròn tâm và bán kính .
Ta có đạt giá trị lớn nhất bằng .
Xét các số phức , thỏa mãn và . Giá trị nhỏ nhất của bằng
	A. 	B. 	C. 	D. 
Hướng dẫn giải
Đặt suy ra 
Và thế vào 
Gọi là hai điểm biểu diễn cho hai số phức 
thuộc đường tròn tâm 
 thuộc đường tròn tâm 
Cho số phức thỏa mãn số phức thỏa mãn Giá trị nhỏ nhất của biểu thức bằng
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi là hai điểm biểu diễn cho hai số phức và .
+) thuộc đường tròn tâm , bán kính .
+) thuộc đường tròn tâm , bán kính .
Vì nên hai đường tròn và ngoài nhau.
.
Vậy giá trị nhỏ nhất của biểu thức bằng .
Cho hai số phức thỏa mãn , . Biết rằng đạt giá trị nhỏ nhất khi , . Tính .
	A. .	B. .	C. 1.	D. .
Hướng dẫn giải
Ta có: + , suy ra tập hợp điểm biểu diễn biểu diễn số phức là đường tròn có tâm , bán kính .
+ , suy ra tập hợp điểm biểu diễn biểu diễn số phức là đường tròn có tâm , bán kính .
Ta có .
+ .
Mặt khác hay .
Suy ra khi thẳng hàng và nằm giữa (Hình vẽ).
Khi đó ta có: và .
Mặt khác ; .
Suy ra .
Cho hai số phức thỏa mãn và Giá trị lớn nhất của biểu thức bằng
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Gọi là hai điểm biểu diễn cho hai số phức và .
+) thuộc đường tròn tâm , bán kính .
+) thuộc đường tròn tâm , bán kính .
Vì nên hai đường tròn và ngoài nhau.
.
Vậy giá trị nhỏ nhất của biểu thức bằng .
Cho hai số phức , thỏa mãn và . Tìm giá trị lớn nhất của biểu thức .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Cách 1
Đặt và suy ra 
Và thế vào 
Và thế vào 
Gọi là hai điểm biểu diễn cho hai số phức 
 thuộc đường tròn tâm 
 thuộc đường tròn tâm 
Cách 2
Ta có 
Gọi là điểm biểu diễn số phức là điểm biểu diễn số phức 
Từ và suy ra điểm nằm trên đường tròn tâm , bán kính , điểm nằm trên đường tròn tâm , bán kính 
Ta có 
Vậy 
Xét các số phức , thỏa mãn và . Giá trị lớn nhất của bằng
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Chọn C
Đặt suy ra 
Và thế vào 
Gọi là hai điểm biểu diễn cho hai số phức 
 thuộc đường tròn tâm 
 thuộc đường tròn tâm 
Vậy .
Cho hai số phức thoả mãn và . Tìm giá trị lớn nhất của biểu thức .
	A. .	B. .	C. .	D. .
 Hướng dẫn giải
Gọi là điểm biểu diễn của số phức .
 có tâm , bán kính .
Gọi là điểm biểu diễn của số phức .
, có tâm , bán kính .
Do nằm ngoài nhau.
. Do đó . Vậy .
DẠNG 8
TẬP HỢP ĐIỂM LÀ HÌNH TRÒN
Trong mặt phẳng phức Oxy, trong các số phức thỏa . Nếu số phức có môđun lớn nhất thì số phức có phần thực bằng bao nhiêu?
	A..	B..	C..	D.
Hướng dẫn giải
Giả sử M là điểm biểu diễn số phức . Xét điểm 
Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính 
. Dấu bằng khi là giao điểm của và 
 (chọn điểm xa O hơn).
Chọn A.
Trong mặt phẳng phức , trong các số phức thỏa . Nếu số phức có môđun lớn nhất thì số phức có phần thực bằng bao nhiêu?
	A..	B..	C..	D..
Hướng dẫn giải
Gọi là điểm biểu diễn số phức 
Gọi là điểm biểu diễn số phức 
Ta có: . Vậy tập hợp điểm biểu diễn số phức là hình tròn tâm như hình vẽ
Để 
 thỏa hệ: 
Trong mặt phẳng phức Oxy, các số phức thỏa . Nếu số phứccó môđun nhỏ nhất thì phần ảo bằng bao nhiêu?
	A..	B..	C..	D.
Hướng dẫn giải
Giả sử M là điểm biểu diễn số phức . Xét điểm 
Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính 
.
Chọn C.
Trong các số phức z thoả mãn . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Tính M + n
	A.	B.	C.	D.
Hướng dẫn giải
Gọi 
, Gọi , đường thẳng OA có phương trình: . 
Xét hệ: 
Gọi là tập hợp các số phức thỏa mãn và . Gọi lần lượt là các số phức có mođun nhỏ nhất và lớn nhất. Tìm số phức .
	A. .	B. .	C. .	D. .
Hướng dẫn giải
Cách 1: Phương pháp hình học
Giả sử .
Ta có	
● . tập hợp các số phức nằm trong hoặc trên đường tròn tâm bán kính .
● . tập hợp các cố phức nằm ngoài hoặc trên đường tròn tâm bán kính .
Dựa vào hình vẽ ta thấy 
. 
Cách 2 : Phương pháp Đại số: Bất đẳng thức số phức
Áp dụng bất đẳng thức .
Ta có 
Dấu thứ xảy ra khi , kết hợp với ta được hệ .
Tương tự cho dấu thứ , ta được .
Số phức thỏa mãn Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 
	A.	B.	C.	D.
Hướng dẫn giải
Cách 1: Phương pháp hình học
Ta có tập hợp các số phức nằm trong hoặc trên đường tròn tâm bán kính .
Gọi . 
Xét : Không có số phức nào thoả mãn.
Xét: .
Vậy tập hợp điểm biểu diễn số phức là hình tròn tâm có bán kính .
Vẽ hình, từ hình .
Cách 2 : Phương pháp Đại số: Bất đẳng thức số phức
Ta có 
Theo tính chất ta có:
Mặt khác suy ra 
Suy ra giá trị lớn nhất và giá trị nhỏ nhất là 
Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức là 
Hằng ngày mình úp đề Toán ôn thi TNPT 12 trên trang trungtamgiasunhatrang.net (trong mục tài liệu môn toán) cho đến ngày 6 tháng 7 năm 2022 sẽ dừng (tầm 70 đề). Bạn đọc theo dõi tải về phục vụ học tập và giảng dạy.
Bạn đọc tải nhiều tài liệu file word toán từ lớp 8 đến 12 tại trungtamgiasunhatrang.net (trong mục tài liệu môn toán) để phục vụ giảng dạy
P/S: Tất cả tài liệu file word đều free
TÀI LIỆU CHẮC CHẮN CÓ SỰ SAI SÓT. MONG BẠN ĐỌC ĐÓNG GÓP ĐỂ HOÀN THIỆN HƠN. 
LIÊN HỆ:https://www.facebook.com/truong.ngocvy.509/