Đề ôn thi khảo sát chất lượng môn Toán Lớp 12 - Đề 7 (Có đáp án)

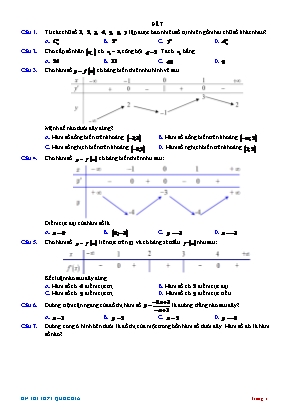
ĐỀ 7
Từ các chữ số , , , , , , lập được bao nhiêu số tự nhiên gồm hai chữ số khác nhau?
A. .	B. .	C. .	D. .
Cho cấp số nhân có , công bội . Ta có bằng
A. .	B. .	C. .	D. .
Cho hàm số có bảng biến thiên như hình vẽ sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng .	B. Hàm số đồng biến trên khoảng .
C. Hàm số nghịch biến trên khoảng .	D. Hàm số nghịch biến trên khoảng .
Cho hàm số có bảng biến thiên như sau:
Điểm cực đại của hàm số là
A. .	B. .	C. .	D. .
Cho hàm số liên tục trên và có bảng xét dấu như sau:
Kết luận nào sau đây đúng
A. Hàm số có điểm cực trị.	B. Hàm số có điểm cực đại.
C. Hàm số có điểm cực trị.	D. Hàm số có điểm cực tiểu.
Đường tiệm cận ngang của đồ thị hàm số là đường thẳng nào sau đây?
A. .	B. .	C. .	D. .
Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
A. .	B. .	C. .	D. .
Đồ thị của hàm số và đồ thị của hàm số có bao nhiêu điểm chung?
A. .	B. .	C. .	D. .
Với là số thực dương tùy ý, bằng
A. .	B. .	C. .	D. .
Tìm đạo hàm của hàm số .
A. .	B. .	C. .	D. .
Giá trị của biểu thức bằng
A. .	B. .	C. .	D. .
Tính tổng các nghiệm của phương trình .
A. .	B. .	C. .	D. .
Tập nghiệm của phương trình là
A. .	B. .	C. .	D. .
Nếu thì hàm số bằng
A. .	B. .
C. .	D. .
Tìm họ nguyên hàm của hàm số .
A. .	B. .
C. .	D. .
Cho . Tính .
A. .	B. .	C. .	D. .
Tính tích phân .
A. .	B. .	C. .	D. .
Mô đun của số phức bằng
A. .	B. .	C. .	D. .
Cho số phức . Số phức có phần ảo là
A. .	B. .	C. .	D. .
Số phức thỏa mãn được biểu diễn trên mặt phẳng tọa độ bởi điểm nào sau đây?
A. .	B. .	C. .	D. .
Cho hình chóp​​ ​​ có đáy​​  là hình vuông cạnh​​ , cạnh bên​​ ​​ vuông góc với đáy và . Tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Một hình lập phương có cạnh bằng . Thể tích của lập phương là bao nhiêu?
A. .	B. .	C. .	D. .
Gọi lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Công thức đúng là:
A. .	B. .	C. .	D. .
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng​​ . Thể tích khối trụ bằng:
A. .	B. .	C. .	D. .
Trong không gian với hệ trục tọa độ , cho hai điểm và . Tọa độ trung điểm của đoạn thẳng là
A. 	B. 	C. 	D. .
Trong không gian với hệ tọa độ , cho mặt cầu . Tìm tọa độ tâm và tính bán kính R của .
A. , .	B. , .
C. , .	D. , .
Trong không gian , cho mặt phẳng Điểm nào dưới đây thuộc ?
A. .	B. .	C. .	D. .
Trong không gian cho điểm và . Vectơ chỉ phương của đường thẳng là
A. 	B. 	C. 	D. 
Gieo một con súc sắc cân đối đồng chất lần. Tính xác suất để tích số chấm xuất hiện trên con súc sắc trong 2 lần gieo là một số lẻ.
A. 	B. 	C. 	D. 
Trong các hàm số sau, hàm số nào đồng biến trên ?
A. .	B. .	C. .	D. .
Tìm giá trị lớn nhất của hàm số trên đoạn .
A. .	B. .	C. .	D. .
Tìm nghiệm của bất phương trình: .
A. .	B. .	C. .	D. .
Cho , . Tính .
A. .	B. .	C. .	D. .
Cho số phức thỏa mãn . Tính mô đun của z.
A. .	B. .	C. .	D. .
Cho hình lập phương cạnh . Gọi là góc giữa và . Chọn khẳng định đúng trong các khẳng định sau?
A. .	B. .	C. .	D. .
Cho hình chóp có đáy là hình vuông cạnh , và . Khoảng cách từ điểm đến mặt phẳng bằng
A. .	B. .	C. .	D. .
Tìm độ dài đường kính của mặt cầu có phương trình .
A. .	B. .	C. .	D. .
Trong không gian , cho và phương trình đường thẳng đi qua hai điểm và là
A. .	B. .
C. .	D. .
Cho hàm số . Biết hàm số có đồ thị như hình bên.
Trên hàm số đạt giá trị nhỏ nhất tại điểm nào?
A. .	B. .	C. .	D. .
Có tất cả bao nhiêu cặp giá trị thực thỏa mãn đồng thời các điều kiện và ?
A. .	B. .	C. .	D. .
Cho hàm số có đạo hàm trên , thỏa mãn .
Tính .
A. .	B. .	C. .	D. .
Có bao nhiêu số phức z thỏa mãn và là một số thuần ảo?
A. 0	B. Vô số	C. 1	D. 2.
Cho hình chóp có đáy là tam giác đều cạnh , . Góc giữa hai mặt phẳng và bằng . Thể tích khối chóp là.
A. .	B. .	C. .	D. .
Cho một tấm nhôm hình vuông cạnh cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng cm, rồi gập tấm nhôm lại như hình vẽ bên để được một cái hộp không nắp. Tìm để hộp nhận được có thể tích lớn nhất.
A. .	B. .	C. .	D. .
Trong không gian , phương trình đường thẳng đi qua song song với : và cắt đường thẳng có phương trình:
A. .	B. .	C. .	D. .
Cho hàm số có bảng biến thiên như sau.
Đồ thị hàm số có bao nhiêu điểm cực trị?
A. .	B. .	C. .	D. .
Tìm tất cả các giá trị thực của tham số để phương trình có ít nhất một nghiệm thuộc đoạn ?
A. .	B. .	C. .	D. .
Cho hàm số bậc ba có đồ thị như hình vẽ, biết đạt cực tiểu tại điểm và thỏa mãn và lần lượt chia hết cho và . Gọi lần lượt là diện tích như trong hình bên. Tính 
A. 	B. 	C. 	D. 
Giả sửlà hai trong các số phức thỏa mãnlà số thực. Biết rằng , giá trị nhỏ nhất của bằng
A. .	B. .	C. .	D. .
Trong không gian với hệ tọa độ , cho mặt cầu và các điểm , . Xét khối nón có đỉnh là tâm của mặt cầu , đường tròn đáy là thiết diện của mặt phẳng với mặt cầu và mặt phẳng đi qua hai điểm , sao cho thể tích của khối nón là lớn nhất. Khi viết phương trình dưới dạng . Tính .
A. .	B. .	C. .	D. .
1.D
2.C
3.D
4.A
5.D
6.B
7.B
8.A
9.C
10.C
11.B
12.B
13.B
14.C
15.D
16.C
17.B
18.D
19.D
20.B
21.D
22.B
23.D
24.D
25.B
26.C
27.D
28.A
29.A
30.B
31.C
32.A
33.D
34.A
35.C
36.C
37.D
38.B
39.D
40.B
41.C
42.C
43.C
44.C
45.A
46.D
47.A
48.A
49.B
50.B
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
 BẢNG ĐÁP ÁN
1.D
2.C
3.D
4.A
5.D
6.B
7.B
8.A
9.C
10.C
11.B
12.B
13.B
14.C
15.D
16.C
17.B
18.D
19.D
20.B
21.D
22.B
23.D
24.D
25.B
26.C
27.D
28.A
29.A
30.B
31.C
32.A
33.D
34.A
35.C
36.C
37.D
38.B
39.D
40.B
41.C
42.C
43.C
44.C
45.A
46.D
47.A
48.A
49.B
50.B
LỜI GIẢI CHI TIẾT
ĐỀ SỐ 26 PHÁT TRIỂN ĐỀ MINH HỌA THI TN 12- 2020-2021
Từ các chữ số , , , , , , lập được bao nhiêu số tự nhiên gồm hai chữ số khác nhau?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn D
Số các số tự nhiên gồm hai chữ số khác nhau được lập từ chữ số trên là: .
Cho cấp số nhân có , công bội . Ta có bằng
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn C
Công thức số hạng tổng quát của cấp số nhân: . 
Ta có: .
Cho hàm số có bảng biến thiên như hình vẽ sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng .	B. Hàm số đồng biến trên khoảng .
C. Hàm số nghịch biến trên khoảng .	D. Hàm số nghịch biến trên khoảng .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn D
Dựa vào bảng biến thiên ta có hàm số nghịch biến trên khoảng .
Cho hàm số có bảng biến thiên như sau:
Điểm cực đại của hàm số là
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn A
Dựa vào bảng biến thiên ta có hàm số đạt cực đại tại điểm .
Cho hàm số liên tục trên và có bảng xét dấu như sau:
Kết luận nào sau đây đúng
A. Hàm số có điểm cực trị.	B. Hàm số có điểm cực đại.
C. Hàm số có điểm cực trị.	D. Hàm số có điểm cực tiểu.
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn D
Dựa vào bảng xét dấu, ta có:
¨ đổi dấu lần khi qua các điểm . 
¨ đổi dấu từ âm sang dương khi qua điểmvà đổi dấu từ dương sang âm khi qua điểm . Suy ra hàm số có điểm cực tiểu.
Đường tiệm cận ngang của đồ thị hàm số là đường thẳng nào sau đây?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn B
, nên đường tiệm cận ngang của đồ thị hàm số đã cho có phương trình là.
Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn B
Đồ thị trên là đồ thị hàm bậc ba (Loại A):
+ Có (Loại D).
+ Đi qua điểm (Loại C).
Đồ thị của hàm số và đồ thị của hàm số có bao nhiêu điểm chung?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn A
Xét phương trình hoành độ giao điểm .
Vậy phương trình (*) có một nghiệm suy ra đồ thị của hai hàm số đã cho có một điểm chung.
Với là số thực dương tùy ý, bằng
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn C
Ta có: .
Tìm đạo hàm của hàm số .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn C
Áp dụng công thức , ta được .
Giá trị của biểu thức bằng
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn B
Ta có: .
Tính tổng các nghiệm của phương trình .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn B
.
Áp dụng định lý Viét ta có tổng các nghiệm của phương trình là .
Tập nghiệm của phương trình là
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn B
Điều kiện: .
Ta có:.
So với điều kiện ta nhận cả 2 nghiệm.
Nếu thì hàm số bằng
A. .	B. .
C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn C
Ta có: .
Tìm họ nguyên hàm của hàm số .
A. .	B. .
C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn D
Xét .
Cho . Tính .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn C
Ta có: .
Tính tích phân .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn B
Ta có: .
Mô đun của số phức bằng
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn D
Cho số phức . Số phức có phần ảo là
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn D
Ta có . 
Vậy phần ảo của là .
Số phức thỏa mãn được biểu diễn trên mặt phẳng tọa độ bởi điểm nào sau đây?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Phan Thanh Phong; GVPB: Trương Minh Mỹ
Chọn B
Vì . 
Do đó điểm biểu diễn số phức là .
Cho hình chóp​​ ​​ có đáy​​  là hình vuông cạnh​​ , cạnh bên​​ ​​ vuông góc với đáy và . Tính thể tích khối chóp .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn D
Diện tích hình vuông​​  là​​ .
Chiều cao khối chóp là​​ .​​
Vậy thể tích khối chóp​​ .
Một hình lập phương có cạnh bằng . Thể tích của lập phương là bao nhiêu?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn B
Khối lập phương có cạnh là thì có thể tích là: .
Gọi lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Công thức đúng là:
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn D
Theo định nghĩa của hình trụ thì chiều cao chính là đường sinh của nó.
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng​​ . Thể tích khối trụ bằng:
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn D
Do thiết diện đi qua trục hình trụ nên ta có .
Bán kính đáy​​ .​​ Do đó thể tích khối trụ ​​.
Trong không gian với hệ trục tọa độ , cho hai điểm và . Tọa độ trung điểm của đoạn thẳng là
A. 	B. 	C. 	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn B
Ta có tọa độ điểm được tính bởi công thức .
Vậy .
Trong không gian với hệ tọa độ , cho mặt cầu . Tìm tọa độ tâm và tính bán kính R của .
A. , .	B. , .
C. , .	D. , .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn C
Mặt cầu có tâm , bán kính .
Trong không gian , cho mặt phẳng Điểm nào dưới đây thuộc ?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn D
Ta có: suy ra .
Trong không gian cho điểm và . Vectơ chỉ phương của đường thẳng là
A. 	B. 	C. 	D. 
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn A
Ta có .
Vậy đường thẳng có một vectơ chỉ phương là .
Gieo một con súc sắc cân đối đồng chất lần. Tính xác suất để tích số chấm xuất hiện trên con súc sắc trong 2 lần gieo là một số lẻ.
A. 	B. 	C. 	D. 
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn A
Số kết quả có thể xảy ra .
Gọi là biến cố “Tích số chấm xuất hiện trên con súc sắc trong lần gieo là một số lẻ “.
.
Trong các hàm số sau, hàm số nào đồng biến trên ?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn B
Do hàm số đồng biến trên nên loại ý C; D vì hai hàm số này không có tập xác định là .
Loại đáp án A vì đây là hàm trùng phương.
Vậy chọn đáp án B.
Tìm giá trị lớn nhất của hàm số trên đoạn .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn C
Hàm số liên tục trên đoạn .
Ta có : , .
.
Vậy .
Tìm nghiệm của bất phương trình: .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn A
Bất phương trình .
Cho , . Tính .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn D
Ta có 
.
Cho số phức thỏa mãn . Tính mô đun của z.
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn A
.
Cho hình lập phương cạnh . Gọi là góc giữa và . Chọn khẳng định đúng trong các khẳng định sau?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn C
Ta có .
Suy ra là hình chiếu vuông góc của lên .
Cho hình chóp có đáy là hình vuông cạnh , và . Khoảng cách từ điểm đến mặt phẳng bằng
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn C
Gọi là giao điểm của và , suy ra .
Từ , kẻ đườngtại . Khi đó .
Xét tam giác vuông tại có là đường cao, , .
Suy ra .
Tìm độ dài đường kính của mặt cầu có phương trình .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn D
Bán kính của mặt cầu: đường kính của mặt cầu là .
Trong không gian , cho và phương trình đường thẳng đi qua hai điểm và là
A. .	B. .	
C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn B
Ta có .
Đường thẳng có đường thẳng chính tắc là .
Cho hàm số . Biết hàm số có đồ thị như hình bên.
Trên hàm số đạt giá trị nhỏ nhất tại điểm nào?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn D
Ta có: . 
.
Vẽ đường thẳng , cắt đồ thị hàm số tại ba điểm , , .
Ta có bảng biến thiên của hàm số trên 
Vậy hàm số đạt giá trị nhỏ nhất trên tại .
Có tất cả bao nhiêu cặp giá trị thực thỏa mãn đồng thời các điều kiện và ?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Nguyễn Bá Trình
Chọn B
Dấu “” xảy ra khi và chỉ khi .
Khi đó .
Kết hợp với điều kiện suy ra .
Với , ta có .
Vậy có đúng cặp số thực thỏa mãn yêu cầu bài toán là và .
Cho hàm số có đạo hàm trên , thỏa mãn .
Tính .
A. .	B. .	C. .	D. .
Lời giải
GVSB : Lương Nguyên Thị; GVPB: Nguyễn Phú Hòa
Chọn C
.
Có bao nhiêu số phức z thỏa mãn và là một số thuần ảo?
A. 0	B. Vô số	C. 1	D. 2.
Lời giải
GVSB : Lương Nguyên Thị; GVPB: Nguyễn Phú Hòa
Chọn C
Giả sử .
Theo bài ra ta có: 
 hay ta có .
Số phức là số thuần ảo nên
.
Vậy có 1 số phức thỏa yêu cầu bài toán.
Cho hình chóp có đáy là tam giác đều cạnh , . Góc giữa hai mặt phẳng và bằng . Thể tích khối chóp là.
A. .	B. .	C. .	D. .
Lời giải
GVSB : Lương Nguyên Thị; GVPB: Nguyễn Phú Hòa
Chọn C
.
Gọi là trung điểm .
Góc giữa hai mặt phẳng và là .
 vuông tại nên .
Thể tích khối chóp là .
Cho một tấm nhôm hình vuông cạnh cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng cm, rồi gập tấm nhôm lại như hình vẽ bên để được một cái hộp không nắp. Tìm để hộp nhận được có thể tích lớn nhất.
A. .	B. .	C. .	D. .
Lời giải
GVSB : Lương Nguyên Thị; GVPB: Nguyễn Phú Hòa
Chọn C
Lời giải
Gọi là cạnh hình vuông bị cắt .
Thể tích của hộp không nắp bằng .
Ta có .
Trên ta có .
Ta có bảng biến thiên:
Từ bảng biến thiên suy ra đạt giá trị lớn nhất tại .
Trong không gian , phương trình đường thẳng đi qua song song với : và cắt đường thẳng có phương trình:
A. .	B. .	C. .	D. .
Lời giải
GVSB : Lương Nguyên Thị; GVPB: Nguyễn Phú Hòa
Chọn A
Ta có: là một vec tơ pháp tuyến của mặt phẳng .
Phương trình tham số của đường thẳng là: .
Gọi là đường thẳng cần tìm. Gọi là giao điểm của và 
Do nên .
.
Phương trình đường thẳng đi qua và nhận là một vec tơ chỉ phương là: .
Cho hàm số có bảng biến thiên như sau.
Đồ thị hàm số có bao nhiêu điểm cực trị?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Ngô Minh Cường; GVPB: Nguyễn Phú Hòa
Chọn D
Xét hàm số 
Ta có 
Bảng biến thiên hàm 
Khi đó bảng biến thiên là
Vậy hàm số có ba cực trị.
Tìm tất cả các giá trị thực của tham số để phương trình có ít nhất một nghiệm thuộc đoạn ?
A. .	B. .	C. .	D. .
Lời giải
GVSB: Ngô Minh Cường; GVPB: Nguyễn Phú Hòa
Chọn A
Với hay hay với .
Khi đó bài toán được phát biểu lại là: “Tìm m để phương trình có 1 nghiệm thuộc đoạn ”.
Ta có pt đề bài .
Xét hàm số:
, 
Suy ra hàm số đồng biến trên .
Khi đó phương trình có nghiệm khi: .
Vậy là các giá trị cần tìm.
Cho hàm số bậc ba có đồ thị như hình vẽ, biết đạt cực tiểu tại điểm và thỏa mãn và lần lượt chia hết cho và . Gọi lần lượt là diện tích như trong hình bên. Tính 
A. 	B. 	C. 	D. 
Lời giải
GVSB: Ngô Minh Cường; GVPB: Nguyễn Phú Hòa
Chọn A
Đặt theo giả thiết có .
Do đó .
Với 
Ta có: 
 là diện tích giới hạn bởi đồ thị ,, 
 là diện tích giới hạn bởi đồ thị , 
Từ .
Giả sửlà hai trong các số phức thỏa mãnlà số thực. Biết rằng , giá trị nhỏ nhất của bằng
A. .	B. .	C. .	D. .
Lời giải
GVSB: Ngô Minh Cường; GVPB: Nguyễn Phú Hòa
Chọn B
Giả sử, .Gọi lần lượt là điểm biểu diễn cho các số phức . Suy ra .
* Ta có . Theo giả thiết là số thực nên ta suy ra . Tức là các điểm thuộc đường tròn tâm , bán kính .
* Xét điểm thuộc đoạn thỏa .
Gọi là trung điểm .
Ta có và .
Từ đó , , suy ra điểm thuộc đường tròn tâm , bán kính .
* Ta có , do đó nhỏ nhất khi nhỏ nhất.
Ta có .
Vậy .
Trong không gian với hệ tọa độ , cho mặt cầu và các điểm , . Xét khối nón có đỉnh là tâm của mặt cầu , đường tròn đáy là thiết diện của mặt phẳng với mặt cầu và mặt phẳng đi qua hai điểm , sao cho thể tích của khối nón là lớn nhất. Khi viết phương trình dưới dạng . Tính .
A. .	B. .	C. .	D. .
Lời giải
GVSB: Ngô Minh Cường; GVPB: Nguyễn Phú Hòa
Chọn B
Mặt cầu có tâm bán kính là .
Ta có , nằm trong mặt cầu. Gọi là hình chiếu của trên và là hình chiếu của lên thiết diện.
Ta có diện tích thiết diện bằng . Do đó thể tích khối nón lớn nhất khi diện tích thiết diện nhỏ nhất hay lớn nhất. Mà suy ra qua và vuông góc với .
Ta có suy ra là trung điểm của . Vậy và .
Vậy .
Vậy .