Đề ôn thi đại học môn Toán - Đề số 4

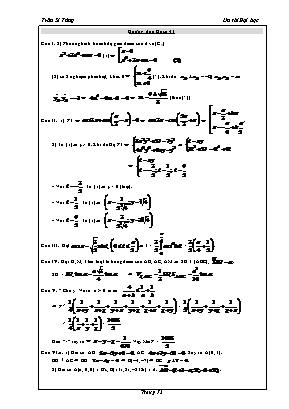
Hướng dẫn Đề số 41
Câu I: 2) Phương trình hoành độ giao điểm của d và (Cm): 
	 (1) Û 
	(2) có 2 nghiệm phân biệt, khác 0 Û (*). Khi đó: 
	 Û Û (thoả (*))
Câu II:	 1) PT Û Û Û .
	2) Từ (1) Þ y ¹ 0. Khi đó Hệ PT Û Þ 
	Û 
	· Với : Từ (1) Þ y = 0 (loại).
	· Với : Từ (1) Þ 
	· Với : Từ (1) Þ 
Câu III: Đặt Þ I = = . 
Câu IV: Gọi H, M, I lần lượt là trung điểm của AB, AC, AM Þ SH ^ (ABC), . 
	SH = 	Þ .
Câu V: · Chú ý: Với a, b > 0, ta có: .
	Þ P £ = 
	 £ = .
	Dấu "=" xảy ra Û . Vậy MinP = .
Câu VI.a: 1) Giả sử: AB: , AC: . Suy ra: A(0; 3). 
	BO ^ AC Þ BO: Þ B(–4; –7) Þ BC: .
	2) Giả sử A(a; 0; 0) Î Ox, B(1+t; 2t; –2+2t) Î d. . 
	Þ . AB = . .
	AB = d(A, (P)) Û Û Þ A(3; 0; 0).
Câu VII.a: Giả sử số thoả mãn là: .
	· Nếu a1 = 1 thì có: (số)
	· Nếu a2 = 1 thì có: (số)	· Nếu a3 = 1 thì có: (số)
	Þ Có tất cả: 840 + 720 + 720 = 2280 (số).
Câu VI.b: 1) (C) có tâm I(3; 0), bán kính R = 2. Giả sử M(0; b) Î Oy. 
	Vì góc giữa hai tiếp tuyến kẻ từ M bằng nên MI = = 4 
	Þ Û Û 	Þ hoặc .
	2) d1 có VTCP , d2 có VTCP . 
	Giả sử Î d1, Î d2.
	AB là đoạn vuông góc chung Û Û Û 
	Þ A(2; 1; 4), B(2; 1; 0).
	Mặt cầu (S) có tâm là trung điểm I(2; 1; 2) của AB và bán kính R = .
	Þ (S): .
Câu VII.b: PT Û Û .
Hướng dẫn Đề số 42
www.VNMATH.com
Câu I: 2) Phương trình đường thẳng MN: . Gọi I(a; b) Î MN Þ 	(1) 
	Phương trình đường thẳng d qua I và vuông góc với MN là: .
	Hoành độ các giao điểm A, B của (C) và d là nghiệm của phương trình: 
	 (x ¹ –1)
	Û (x ¹ –1)
	A, B đối xứng nhau qua MN Û I là trung điểm của AB. 
	Khi đó: Û 	(2)
	Từ (1) và (2) ta được: Û 
	Suy ra phương trình đường thẳng d: Þ A(2; 0), B(0; –4).
Câu II:	 1) PT Û (*). 
	Ta có: . Do đó (*) Û Û Û .
	2) PT Û (1). Ta thấy không phải là nghiệm của (1).
	Với , ta có: (1) Û Û 
	Đặt . Ta có: 
	Do đó f(x) đồng biến trên các khoảng và Þ Phương trình f(x) = 0 có nhiều nhất 1 nghiệm trên từng khoảng .
	Ta thấy là các nghiệm của f(x) = 0. Vậy PT có 2 nghiệm .
Câu III: Ta có: .
	Do đó: I = = 
	 = 
	Đặt Þ 	
	Þ I = = .
Câu IV: Trên AC lấy điểm D sao cho: DS ^ SC (D thuộc đoạn AC) Þ .
	Ta có: Þ Þ 
	Þ = 
	và	 = 
	Þ SD = 
	Mặt khác, Þ 
	 = 
	Mà Þ 
	Vậy: .
Câu V: Đặt Þ 
	Þ P = = 
	Đặt . 
	Khi đó: P = = = 
	Dấu "=" xảy ra Û Û . Vậy MinP = khi .
Câu VI.a: 1) Giả sử A(a; –a –1) Î d1, B(b; 2b – 1) Î d2. 
	 Û Û Þ A(0; –1), B(3; 5) 
	Þ Phương trình d: .
	2) PTTS của AB: Þ Giao điểm của AB với (P) là: M(7; –3; 1)
	Gọi I là hình chiếu của B trên (P). Tìm được I(3; 0; 2). Hình chiếu d của đường thẳng AB là đường thẳng MI.
	Þ Phương trình đường thẳng d là: 
Câu VII.a: PT có các nghiệm Þ .
Câu VI.b: 1) (C) có tâm I(1; 1) và bán kính R = . IM = 
	Þ M nằm trong đường tròn (C).
	Giả sử d là đường thẳng qua M và H là hình chiếu của I trên d. 
	Ta có: AB = 2AH = .
	Dấu "=" xảy ra Û H º M hay d ^ IM. Vậy d là đường thẳng qua M và có VTPT 
	Þ Phương trình d: .
	2) Phương trình mp(ABC): . Gọi H(x; y; z) là trực tâm của DABC.
	Ta có: Û Û Þ .
Câu VII.b: Phương trình Û Û 
	Số hạng thứ 6 trong khai triển là: 
	Ta có: Û 
	Û 
	Û Û Û 
Hướng dẫn Đề số 43
www.VNMATH.com
Câu I: 2) Giao điểm của hai tiệm cận là I(1; 2). Gọi M(a; b) Î (C) Þ (a ¹ 1)
	Phương trình tiếp tuyến của (C) tại M: 
	Phương trình đwòng thẳng MI: 
	Tiếp tuyến tại M vuông góc với MI nên ta có: Û 
	Vậy có 2 điểm cần tìm M1(0; 1), M2(2; 3)
Câu II:	 1) PT Û 
	Đặt , 
	PT trở thành: Û Û 	Û 
	· Với 
	· Với 
	· Với 
	2) Điều kiện: Û x ³ 1. 
	Khi đó: 	(do x ³ 1)
	Þ VT > = 2
	Þ PT vô nghiệm.
Câu III: Phương trình tung độ giao điểm của (C) và (d): Û 
	V = = 
Câu IV: Gọi N = BM Ç AC Þ N là trọng tâm của DABD. 
	Kẻ NK // SA (K Î SC). Kẻ KI // SO (I Î AC) Þ KI ^ (ABCD). Vậy 
	Ta có: DSOC ~ DKIC Þ (1),	DKNC ~ DSAC Þ 	(2)
	Từ (1) và (2) Þ Þ 
	Ta có: DADC đều Þ CM ^ AD và CM = Þ SBCDM = 
	Þ VK.BCDM = 
Câu V: Ta có . Ta cần chứng minh: .
	Thật vậy, áp dụng BĐT Cô–si ta có: 
	Þ Þ Þ 	(1)
	Tương tự:	(2),	(3)
	Do đó: 	
	Dấu "=" xảy ra Û .
Câu VI.a: 1) Tam giác OAB có diện tích lớn nhất Û DOAB vuông cân tại O. 
	Khi đó .
	Giả sử phương trình đường thẳng d: 
	Ta có: Û Û 
	Û 
	· Với : chọn A = 47 Þ B = 
	Þ d: 
	· Với : chọn A = 47 Þ B = 
	Þ d: 
	2) (P) có VTPT . Giả sử A¢(x; y; z). 
	Gọi I là trung điểm của AA¢ Þ .
	Ta có: A¢ đối xứng với A qua (P) Û Û 
	Û . 	Vậy: 	A¢(–4; –3; –2).
Câu VII.a: Số các số gồm 6 chữ số khác nhau lập từ các số 1, 2, 3, 4, 5, 6 là: 	6! (số)
	Số các số gồm 6 chữ số khác nhau mà có 2 số 1 và 6 đứng cạnh nhau là: 	2.5! (số)
	Þ Số các số thoả yêu cầu bài toán là:	6! – 2.5! = 480 (số)
Câu VI.b: 1) Ta có A = AD Ç AM Þ A(9; –2). Gọi C¢ là điểm đối xứng của C qua AD Þ C¢ Î AB.
	Ta tìm được: C¢(2; –1). Suy ra phương trình (AB): Û .
	Viết phương trình đường thẳng Cx // AB Þ (Cx): 
	Gọi A¢ = Cx Ç AM Þ A¢(–17; 6). M là trung điểm của AA¢ Þ M(–4; 2)
	M cũng là trung điểm của BC Þ B(–12; 1).
	2) Giả sử Î d1, Î d2.
	Þ 
	AB // Oz Û Û Û Þ 
	Þ Phương trình đường thẳng AB: 
Câu VII.b: 
	· (1) Û . Đặt f(x) = . Ta có: f¢(x) = 
	Þ f(x) đồng biến. Mặt khác f(2) = 0, nên nghiệm của (1) là: S1 = [2; +¥)
	· (2) Û Û Û 	(*)
	· Hệ có nghiệm Û (*) có nghiệm thuộc [2; +¥)
	Đặt g(x) = . Ta có: g¢(x) = > 0, "x ³ 2 Þ g(x) đồng biến trên [2; +¥) và g(2) = .
	Do đó (*) có nghiệm thuộc [2; +¥) Û .
	Vậy để hệ có nghiệm thì .
Hướng dẫn Đề số 44
www.VNMATH.com
Câu I: 2) TXĐ: D = R \ {1}. 
	Để đồ thị tiếp xúc với đường thẳng thì: 
	Từ (**) ta có Û 
	· Với x = m, thay vào (*) ta được: (thoả với mọi m). Vì x ¹ 1 nên m ¹ 1.
	· Với x = 2 – m, thay vào (*) ta được: Û 	Û Þ x = 1 (loại)
	Vậy với m ¹ 1 thì đồ thị hàm số tiếp xúc với đường thẳng .
Câu II:	 1) PT Û Û Û 
	2) . 	Điều kiện: .
	(1) Û Û Û 	(vì nên )
	Thay vào (2) ta được: Û Û 
	Vậy hệ có 2 nghiệm: (1; 0), (–2; 3).
Câu III: Đặt Þ dt = –dx. Ta có I = = 
	Þ 2I = + = = 
	 = = 1 . Vậy: I = .	
Câu IV: Vì ABB¢A¢ là hình bình hành nên ta có: . 
	Mà 
	Vậy, .
Câu V: Ta có: P = 
	Xét . 
	Ta có: Þ 
	Suy ra: P ³ . Dấu "=" xảy ra Û cùng hướng hay y = 0.
	Mặt khác, áp dụng BĐT Bunhiacôpxki ta có: 
	 Þ . 	Dấu "=" xảy ra Û .
	Do đó: P ³ ³ . Dấu "=" xảy ra Û .
	Vậy MinP = khi .
Câu VI.a: 1) Ta có: Þ . Gọi M(x; y) Î (E). 
	Ta có: .
	Ta có: 
	Û Û x = 0 (y= ± 5)
	Vậy có 2 điểm thoả YCBT: M1(0; 5), M2(0; –5).
	2) Gọi I là điểm thoả: Þ 
	Ta có: T = 
	Do đó: T nhỏ nhất Û nhỏ nhất Û M là hình chiếu của I trên (P).
	Ta tìm được: .
Câu VII.a: Ta có: 
	Þ 
	Þ .
Câu VI.b: 1) (C) có tâm I(3; 4). 
	· Ta có: Þ AI là đường trung trực của BC. DABC vuông cân tại A nên AI cũng là phân giác của . Do đó AB và AC hợp với AI một góc .
	· Gọi d là đường thẳng qua A và hợp với AI một góc . Khi đó B, C là giao điểm của d với (C) và AB = AC.
	Vì ¹ (1; 1), (1; –1) nên d không cùng phương với các trục toạ độ Þ VTCP của d có hai thành phần đều khác 0. Gọi là VTCP của d. Ta có:
	 Û Û 
	· Với a = 3, thì Þ Phương trình đường thẳng d: . 
	Ta tìm được các giao điểm của d và (C) là: 	
	· Với a = , thì Þ Phương trình đường thẳng d: . 
	Ta tìm được các giao điểm của d và (C) là: 	
	· Vì AB = AC nên ta có hai cặp điểm cần tìm là: 	
	và	
	2) Gọi H là hình chiếu của M trên d. Ta có: MH = .
	Tam giác ABM đều, nhận MH làm đường cao nên: MA = MB = AB = 
	Do đó, toạ độ của A, B là nghiệm của hệ: . 
	Giải hệ này ta tìm được:	.
Câu VII.b: 
	Điều kiện: . Từ (2) ta có: Þ .
	(1) Û Û .
	Xét hàm số: f(t) = (t > 0). Ta có: f ¢(t) = 
	Þ f(t) đồng biến khi t > 0	Þ f(x) = f(2y) Û x = 2y 
	Thay x = 2y vào (2) ta được: Û 
	Vậy nghiệm của hệ là: .
Hướng dẫn Đề số 45
www.VNMATH.com
Câu I: 2) Gọi là toạ độ của tiếp điểm.
	Tam giác OAB cân tại O nên tiếp tuyến song song với một trong hai đường thẳng hoặc .
	Þ Û Þ 
	· Với Þ D: (loại)	· Với Þ D: (nhận)
	Vậy phương trình tiếp tuyến cần tìm là: .
Câu II:	 1) Điều kiện: Û 
	PT Û Û 
	Û Û 
	Û . 	Vậy PT có nghiệm: .
	2) Điều kiện: . Đặt Þ .
	Ta có hệ PT: . Giải hệ này ta được Þ Û .
	Thử lại, ta thấy là nghiệm của PT. Vậy PT có nghiệm .
Câu III: I = = A – B.	
	· A = = = 
	· B = = 
	Vậy I = – .
Câu IV: Gọi E là trung điểm của AB Þ BC = .	Ta có: 
	Trong tam giác BIC, kẻ đường cao IF, ta có: IF = .
	Từ giả thiết Þ SI ^ (ABCD) Þ Þ SI = 
	Þ Thể tích khối chóp S.ABCD:	.
Câu V: Xét điều kiện:	 Þ 
	Þ (*)	
	Đặt (u, v > 0). Từ (*) Þ Þ 	(1)
	Khi đó ta có: BĐT Û Û 
	Û Û 	(2) (do (1))
	Mặt khác từ (1) ta có: 	 (3)
	và Þ Þ 	(4)
	Từ (3) và (4) ta suy ra được điều cần chứng minh (2).
Câu VI.a: 1) Giả sử E(a; 5 – a) Î D Þ 
	Gọi P là điểm đối xứng của E qua I Þ P(12 – a; a – 1), 
	Ta có: Û Û 
	Đường thẳng đi qua M(1; 5) và nhận làm VTPT.
	· Với Þ Þ Phương trình AB: 
	· Với Þ Þ Phương trình AB: 
	2) (S) có tâm I(1; 2; 3), bán kính R = 5
	 Þ (P) cắt (S) theo một đường tròn (C).
	Dễ xác định tâm đường tròn (C) là J(3; 0; 2) và bán kính là r = 4.
Câu VII.a: PT có các nghiệm: 
	Þ A = = 20
Câu VI.b: 1) (C) có tâm I(–2; –2), bán kính R = .
	Ta có: 
	Dấu "=" xảy ra Û Û Û DAIB vuông cân tại I
	Khi đó: Û Û Û 
	2) Giả sử: Î D1.
	Khoảng cách từ M đến D2: 
	Khoảng cách từ M đến mặt phẳng (P): 
	Từ đó ta có:	 = 
	Û Û 
	· Với t = 1 Þ M(0; 1; –3)	· Với t = Þ 
Câu VII.b: Điều kiện: 
	Hệ PT Û Û Û 
	vậy hệ phương trình có 2 nghiệm: (2; 2), (–2; –2).
Hướng dẫn Đề số 46
www.VNMATH.com
Câu I: 2) PTTT của (C) tại điểm là: 
	D qua O Þ Các tiếp tuyến cần tìm: , .
Câu II:	 1) PT Û 
	Û . 
 	KL: nghiệm PT là .
	2) Ta có: 
	Khi thì hệ VN. 
 	Khi , chia 2 vế cho ta được: 
	Đặt , ta có : 
Câu III: Ta có: nên PT 
	Xét 
	Kết luận:	
Câu IV: Gọi O là giao điểm AC và BD . 
	Ta có: 
	Gọi M, N là trung điểm AB và CD và I là tâm đường tròn nội tiếp tam giác SMN. Ta chứng minh 	I cách đều các mặt 	của hình chóp
Câu V: Đặt . Ta có: 
	Và . 
	Suy ra : .	Điều kiện:.
 	Do đó: , 
 	 và .
	Kết luận: Max P = và Min P = 
Câu VI.a: 1) PT 
	Û 
	2) Ta có: . Đặt 
 	Suy ra : = 
Câu VII.a: Gọi M là hình chiếu của lên Oy, ta có: . 
	 là bán kính mặt cầu cần tìm.
	Kết luận: PT mặt cầu cần tìm là .
Câu VI.b: 1) Điều kiện : x > 0 . BPT 
	Đặt . Ta có: hoặc Û hoặc .
	2) Ta có: . Hàm số có 2 cực trị có 2 nghiệm phân biệt, khác 0 
	Khi đó các điểm cực trị là: 
	. Dấu "=" xảy ra Û. Kết luận: .
Câu VII.b: . Hệ số góc của tiếp tuyến (D) cần tìm là . 
	Þ PT (D) có dạng hoặc 
	· tiếp xúc (C) . 
	Kết luận: 
	· tiếp xúc (C) . 
	Kết luận: .
Hướng dẫn Đề số 47
www.VNMATH.com
Câu I: 2) Phương trình HĐGĐ của đồ thị (1) và trục Ox: (*).
	Đặt , ta có : (**)
	Ta có : và với mọi . Nên PT (**) có nghiệm dương.
	Þ PT (*) có ít nhất 2 nghiệm phân biệt (đpcm).
Câu II:	 1) PT .
	Û Û 
	Û 
	2) . 
	Từ (1) Þ , nên (2) Û (vì y ¹ 0)
	Xét 
	Dựa vào BTT ta kết luận được hệ có nghiệm duy nhất .
Câu III: Ta có: Þ
Câu IV: Gọi T là giao điểm của MN với CD; Q là giao điểm của PT với AD.
 	Vẽ DD¢ // BC, ta có: DD¢=BM .
	Mà: 
	Nên: 	(1)
	Và: 	(2).
	Từ (1) và (2), suy ra : .
	Kết luận: Tỉ số thể tích cần tìm là hoặc .
Câu V: Áp dụng BĐT Cô-si ta có: (1). Dấu bằng xảy ra Û.
	Tương tự: 	(2) 	và 	 	(3).
	Mà: (4). Cộng (1),(2),(3),(4), ta có: . 
	Dấu "=" xảy ra Û . 	Vậy GTNN của P là 19 khi .
Câu VI.a: 1) Điều kiện : . 
	PT Û Û Û Û 
	2) Ta có: . Do đó: 
	Suy ra tọa độ các điểm trên đồ thị có hoành độ và tung độ là những số nguyên là 
	Kết luận: Phương trình đường thẳng cần tìm là: .
Câu VII.a: Gọi là tâm đường tròn cần tìm.
	Ta có:.
	· thì phương trình đường tròn là: .
	· thì phương trình đường tròn là: .
Câu VI.b: 1) Điều kiện :. Đặt , ta có : 
	BPTÛ .
	2) Ta có: .
	 ; y¢¢ đổi dấu qua . 
 	Suy ra: là điểm uốn.
	Để điểm uốn U nằm trên đồ thị hàm số thì Û 
Câu VII.b: Ta có: Þ đều. Do đó tâm I của đường tròn ngoại tiếp là trọng tâm của nó.
	Kết luận: .
Hướng dẫn Đề số 48
www.VNMATH.com
Câu I: 2) Gọi d là đường thẳng qua I và có hệ số góc k Þ PT .
 	Ta có: d cắt ( C) tại 2 điểm phân biệt M, N có 2 nghiệm phân biệt khác .
	Hay: có 2 nghiệm phân biệt khác 	
	Mặt khác: I là trung điểm MN với .
	Kết luận: PT đường thẳng cần tìm là với .
Câu II:	 1) PT 	 
 Û 
	2) Ta có : .
	· Khi: , ta có: và 
	Suy ra: là các nghiệm của phương trình: 
	Vậy nghiệm của Hệ PT là: 
	 hoặc .
	· Khi: , ta có: và 
 	Suy ra: là nghiệm của phương trình: 
Câu III: Đặt . Điều kiện: . 
	PT trở thành: Û 
	Xét hàm số: 
	. Dựa vào BBT, ta kết luận .
Câu IV: Gọi M là trung điểm BC, hạ AH vuông góc với A¢M. 
	Ta có: .
	Mà .
	Mặt khác: .
	Kết luận: 	.
Câu V: Ta có: 	(1)
	Tương tự: 	(2),	 	(3).
	Cộng (1), (2), (3), ta có: 
Câu VI.a: 1) Điều kiện: . 
	BPT 
	 Û hay 
	So sánh với điều kiện. Kết luận: Nghiệm của BPT là .
	2) Đặt . Suy ra : 
Câu VII.a: Gọi là giao điểm của d với Ox, Oy, suy ra: . 
	Theo giả thiết, ta có: Û .
	· Khi thì . Nên: .
	· Khi thì . Ta có: . 
 	+ Với 
	+ Với . 
Câu VI.b: 1) 	(*).
	Từ (1) ta có: 
	· Khi: thì (*) Û Û .
	· Khi: thì (*) Û Û 
	2) Ta có: Þ 
Câu VII.b: PTCT elip (E) có dạng: .
	Ta có: Û .	Vậy (E): 
Hướng dẫn Đề số 49
www.VNMATH.com
Câu I: 2) Tiếp tuyến của đồ thị (C) tại điểm M có hoành độ thuộc đồ thị (C) có phương trình: 
	Tâm đối xứng . 
	Ta có 
	 lớn nhất Û
	Từ đó suy ra có hai tiếp tuyến và .
Câu II:	 1) Điều kiện 
	Để ý rằng: 
Khi đó PT trở thành: 
 	: Không thoả điều kiện (*).
	Vậy phương trình đã cho vô nghiệm.
	2) Điều kiện: 
 	Đặt . Hệ PT trở thành: 
 	Thay (2) vào (1) ta được: 
	· Nếu v = 3 thì u = 9, ta có Hệ PT: 
 	· Nếu thì u = 7, ta có Hệ PT: 
	So sánh điều kiện ta được 4 nghiệm của Hệ PT.
Câu III: Đặt 
	· Tính . Đặt 
	Từ đó .
Câu IV: Kẻ SO ^ (ABCD) thì O là giao điểm của AC và BD. Gọi I, J lần lượt là trung điểm của AB và CD; G là trọng tâm SAC .
	Góc giữa mặt bên (SCD) và đáy (ABCD) là Þ DSIJ đều cạnh a Þ G cũng là trọng tâm DSIJ.
	IG cắt SJ tại K là trung điểm của SJ; M, N là trung điểm của SC, SD.
	; 
	Suy ra: .
Câu V: Vì nên 
	Tương tự : 
	Cộng các BĐT (1), (2), (3) vế theo vế ta được: 
	Sử dụng BĐT (4) và BĐT Cô–si ta có: 
	Cũng theo BĐT Cô–si ta có : 
	Do đó: (đpcm)
	Dấu "=" xảy ra Û a = b = c = 1.
Câu VI.a: 1) Gọi I là trung điểm của BC. Ta có 
 	Đường thẳng BC qua I vuông góc với AH có phương trình: 
	Vì là trung điểm của BC nên giả sử thì và 
	H là trực tâm của tam giác ABC nên ; 
	Vậy hoặc 
	2) có tâm và R = 5.
 	Khoảng cách từ I đến (a) là: 	Þ (a) và mặt cầu (S) cắt nhau.
	Gọi J là điểm đối xứng của I qua (a). Phương trình đường thẳng IJ : 
	Toạ độ giao điểm H của IJ và (a) thoả 
	Vì H là trung điểm của IJ nên .
	Mặt cầu (S¢) có tâm J bán kính R¢ = R = 5 nên có phương trình: 
Câu VII.a: Có 2 trường hợp xảy ra:
	· Trường hợp 1: Đội tuyển có Vũ Mạnh Cường, không có Ngô Thu Thuỷ
	Số cách chọn 3 nam còn lại là .
 	Số cách chọn 3 nữ không có Ngô Thu Thuỷ là .
	Suy ra số cách chọn trong trường hợp này là (cách)
	· Trường hợp 2: Đội tuyển có Ngô Thu Thuỷ, không có Vũ Mạnh Cường
	Số cách chọn 4 nam không có Vũ Mạnh Cường là 
 	Số cách chọn 2 nữ còn lại là 
	Suy ra số cách chọn trong trường hợp này là (cách)
	Vậy số cách chọn đội tuyển bóng bàn Quốc gia là: 1680 + 540 = 2220 (cách)
Câu VI.b: 1) Ta có AC vuông góc với BH và đi qua M(1; 1) nên có phương trình: .
 	Toạ độ đỉnh A là nghiệm của hệ : 
	Vì M là trung điểm của AC nên 
	Vì BC đi qua C và song song với d nên BC có phương trình: 
	2) Do ABCD là hình thang cân nên AD = BC = 3.
	Gọi là đường thẳng qua C và song song với AB, (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của và (S).
	Đường thẳng có vectơ chỉ phương nên có phương trình: 
 	Phương trình mặt cầu 
	Toạ độ điểm D thoả Hệ PT: 
	· Với t = – 1, thì D(4; – 3; 0) : không thoả vì AB = CD = 7
	· Với (nhận)
Câu VII.b: 
	Ta có: 
	· Với x = 0 thay vào (1) ta được: 
	· Với thay vào (1) ta được : 
	Đặt , vì nên . Khi đó: 
	(3) : 
	Suy ra: ; 
	Vậy Hệ PT đã cho có 2 nghiệm và 
Hướng dẫn Đề số 50
Câu I: 2) 
	· Khi m = 0 thì (1) đồng biến trên R thoả yêu cầu bài toán.
	· Khi thì (1) có 2 cực trị 
	Do đó đồ thị cắt Ox tại duy nhất 1 điểm khi: 
	Kết luận: khi thì đồ thị của (1) cắt Ox tại duy nhất một điểm.
Câu II:	 1) PT Û Û 
	 Û Û Û 
	2) . Điều kiện : 
	Ta có: (1) Û 
	· Với , thế vào (2) ta được : 
	Þ Hệ có nghiệm 
	· Với , thế vào (2) ta được : Vô nghiệm.
	Kết luận: hệ phương trình có 2 nghiệm là: 
Câu III: . Đặt 
 	Đổi cận: 
	Ta được = 
Câu IV: Kẻ đường cao SH, gọi I là trung điểm BC. Giả thiết cho .
	Gọi x là độ dài cạnh của DABC. Suy ra :
	DSAH vuông tại H 
	DSHI vuông cân tại H 
	Suy ra: 
	Do đó: 
Câu V: Gọi . Đặt thì 
	Với 
	Ta có: 
	 (đpcm)
Câu VI.a: 1) Ta có và . 
	Phương trình các đường phân giác của các góc tạo bởi , là: 
	D1: và D2: 
	tạo với , một tam giác vuông cân vuông góc với D1 hoặc D2.. 	
 	Þ Phương trình của có dạng: hay 
	Mặt khác, qua nên C = 25 ; C¢ = 77
	Suy ra : hay 
	Theo giả thiết tam giác vuông cân có diện tích bằng Þ cạnh huyền bằng 
	Suy ra độ dài đường cao A H == 
	· Với thì ( thích hợp)
	· Với thì ( loại )
	2) Theo giả thiết mp(Oxy) và (P): vuông góc với trục Oz , cắt mặt cầu theo 2 đường tròn tâm , bán kính và tâm , bán kính. Suy ra tâm mặt cầu (S) là Î Oz.
	R là bán kính mặt cầu thì : Û 
	Þ , 
	Vậy phương trình mặt cầu (S) : 
Câu VII.a: Û n = 6 và n = – 3 ( loại )
	Khi đó: 
	Ta có : 
	Nên 
	Û Û 
 	Vậy a = 1 và n = 6 .
Câu VI.b: 1) (C) có tâm và bán kính R = 5. 
	Gọi H là trung điểm dây cung AB thì AH = 4 và hay (*)
	(D) qua gốc tọa độ nên phương trình có dạng: 
	Từ (*) cho : Û hay 
	· Với , chọn A = 3; B = – 4 Þ Phương trình của (D): 
	· Với A = 0, chọn B = 1 Þ Phương trình của (D): .
	Kết luận : PT của (D) là hay .
	2) (D) qua điểm A(1;0;0) và có VTCP . (P) có VTPT .
	Giao điểm M(0;0;m) cho . (a) có VTPT 
	(a) và (P): tạo thành góc 600 nên :
 	Û.
	Kết luận : hay 
Câu VII.b: PT 
	Đặt : , ; 
	; 
	Kết luận : Khi thì PT có nghiệm .