Đề ôn tập học sinh giỏi Toán 7 – Số 4, 5, 6

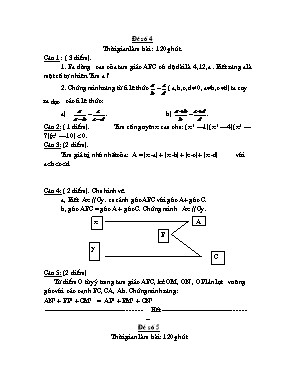
Đề số 4
Thời gian làm bài : 120 phút.
Câu 1 : ( 3 điểm).
	1. Ba đường cao của tam giác ABC có độ dài là 4,12 ,a . Biết rằng a là một số tự nhiên. Tìm a ?
	2. Chứng minh rằng từ tỉ lệ thức ( a,b,c ,dạ 0, aạb, cạd) ta suy ra được các tỉ lệ thức:
	a) .	b) .
Câu 2: ( 1 điểm).	Tìm số nguyên x sao cho: ( x2 –1)( x2 –4)( x2 –7)(x2 –10) < 0.
Câu 3: (2 điểm).
	Tìm giá trị nhỏ nhất của: A = | x-a| + | x-b| + |x-c| + | x-d| với a<b<c<d.
Câu 4: ( 2 điểm). Cho hình vẽ.
	a, Biết Ax // Cy. so sánh góc ABC với góc A+ góc C.
	b, góc ABC = góc A + góc C. Chứng minh Ax // Cy. 
x
A
B
y
C
Câu 5: (2 điểm) 
 Từ điểm O tùy ý trong tam giác ABC, kẻ OM, ON , OP lần lượt vuông góc với các cạnh BC, CA, Ab. Chứng minh rằng:
AN2 + BP2 + CM2 = AP2 + BM2 + CN2
---------------------------------------------- Hết ------------------------------------------
Đề số 5
Thời gian làm bài: 120 phút
Câu 1(2đ):
	a) Tính: A = 1 + 
	b) Tìm n Z sao cho : 2n - 3 n + 1
Câu 2 (2đ):
	a) Tìm x biết: 3x - = 2
	b) Tìm x, y, z biết: 3(x-1) = 2(y-2), 4(y-2) = 3(z-3) và 2x+3y-z = 50.
Câu 3(2đ): 	Ba phân số có tổng bằng , các tử của chúng tỉ lệ với 3; 4; 5, các mẫu của chúng tỉ lệ với 5; 1; 2. Tìm ba phân số đó.
Câu 4(3đ):	Cho tam giác ABC cân đỉnh A. Trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là trung điểm của DE. Chứng minh ba điểm B, I, C thẳng hàng.
Câu 5(1đ):	Tìm x, y thuộc Z biết: 2x + = 
---------------------------------------------------Hết----------------------------------------------
Đề số 6
Thời gian làm bài: 120’.
Câu 1: Tính :
	a) A = .
	b) B = 1+ 
Câu 2:
	a) So sánh: và .
	b) Chứng minh rằng: .
Câu 3:
 Tìm số có 3 chữ số biết rằng số đó là bội của 18 và các chữ số của nó tỉ lệ theo 1:2:3
Câu 4
 Cho tam giác ABC có góc B và góc C nhỏ hơn 900 . Vẽ ra phía ngoài tam giác ấy các tam giác vuông cân ABD và ACE ( trong đó góc ABD và góc ACE đều bằng 900 ), vẽ DI và EK cùng vuông góc với đường thẳng BC. Chứng minh rằng:
	a. BI=CK; EK = HC; b. BC = DI + EK.
Câu 5:	Tìm giá trị nhỏ nhất của biểu thức : A = 
------------------------------------------ hết ---------------------------------------------