Đề ôn tập học kỳ II Toán lớp 7

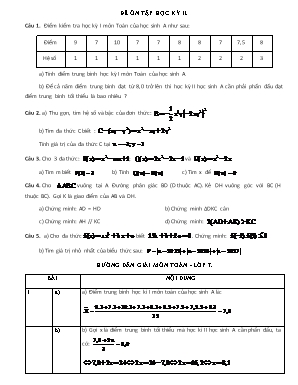
ĐỀ ÔN TẬP HỌC KỲ II.
Câu 1. Điểm kiểm tra học kỳ I môn Toán của học sinh A như sau:
Điểm
9
7
10
7
7
8
8
7
7,5
8
Hệ số
1
1
1
1
1
1
2
2
2
3
a) Tính điểm trung bình học kỳ I môn Toán của học sinh A.
b) Để cả năm điểm trung bình đạt từ 8,0 trở lên thì học kỳ II học sinh A cần phải phấn đấu đạt điểm trung bình tối thiểu là bao nhiêu ? 
Câu 2. a) Thu gọn, tìm hệ số và bậc của đơn thức: 
b) Tìm đa thức C biết : 
Tính giá trị của đa thức C tại 
Câu 3. Cho 3 đa thức: ; và 
	a) Tìm m biết 	b) Tính 	c) Tìm x để 
Câu 4. Cho vuông tại A. Đường phân giác BD (D thuộc AC). Kẻ DH vuông góc với BC (H thuộc BC). Gọi K là giao điểm của AB và DH.
	a) Chứng minh: AD = HD	b) Chứng minh ∆DKC cân
	c) Chứng minh: AH // KC	d) Chứng minh: 
Câu 5. a) Cho đa thức biết . Chứng minh: 
	b) Tìm giá trị nhỏ nhất của biểu thức sau: 
HƯỚNG DẪN GIẢI MÔN TOÁN - LỚP 7.
BÀI
NỘI DUNG
1
a)
a) Điểm trung bình học kì I môn toán của học sinh A là:
b)
b) Gọi x là điểm trung bình tối thiểu mà học kì II học sinh A cần phấn đấu, ta có: 
Vậy học sinh A học kì II cần phải phấn đấu đạt điểm trung bình tối thiểu là: 8,1
2
a)
a) 
Hệ số của đơn thức là: -2
Bậc của đơn thức: 10.
b)
b) 
Thay vào đa thức C ta được: 
Vậy với thì C = 2
3
a)
a) 
Giải tìm được m = -1
Vậy m = -1.
b)
b) 
c)
c) 
 hoặc 
Vậy hoặc 
4
Hình vẽ
a)
a) Chứng minh: 
 (đpcm)
b)
b) Chứng minh: 
 cân tại D
c)
c) Chứng minh: D là trực tâm của , suy ra BD là đường cao ứng với cạnh KC (1)
Ta có: , suy ra BD là trung trực của AH (2)
Từ (1) và (2) suy ra AH // BD (đpcm)
d)
d) Theo BĐT tam giác ta có: 
Mà AK = HC; AD = DH (đpcm)
5
a)
a) Ta có ; 
 (đpcm)
b)
b) 
 Vì: 
 Mà: 
 Dấu bằng xảy ra 
 Vậy P đạt giá trị nhỏ nhất bằng 2 khi