Đề kiểm tra học kỳ I môn Toán Lớp 8 (Kết nối tri thức và cuộc sống) - Năm học 2023-2024 - Trường TH và THCS Đại Chánh (Có đáp án)

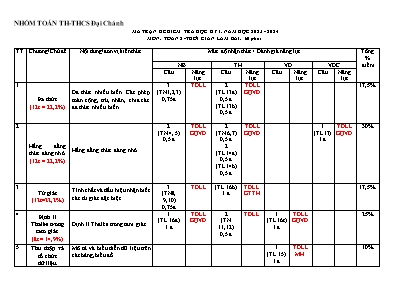
NHÓM TOÁN TH-THCS Đại Chánh
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I. NĂM HỌC 2023 - 2024
MÔN: TOÁN 8 -THỜI GIAN LÀM BÀI: 60 phút
TT

Chương/Chủ đề

Nội dung/đơn vị kiến thức

Mức độ nhận thức + Đánh giá năng lực

Tổng
% điểm

NB
TH
VD
VDC
Câu
Năng lực
Câu
Năng lực
Câu
Năng lực
Câu
Năng lực
1
Đa thức
(12t = 22,2%)
Đa thức nhiều biến. Các phép toán cộng, trừ, nhân, chia các đa thức nhiều biến

3
(TN1,2,3)
0,75 đ
TDLL
2
(TL 13a)
0,5 đ
(TL13b)
0,5 đ

TDLL
GQVĐ




17,5%
2
Hằng đẳng thức đáng nhớ.
(12t = 22,2%)
Hằng đẳng thức đáng nhớ.

2
(TN 4, 5)
0,5 đ
TDLL
GQVĐ
2
(TN 6,7)
0,5 đ
2
(TL 14a)
0,5 đ
(TL14b)
0,5 đ

TDLL
GQVĐ


1
(TL17)
1 đ
TDLL
GQVĐ
30%
3
Tứ giác
(12t=22,2%)
Tính chất và dấu hiệu nhận biết các tứ giác đặc biệt.

3
(TN8, 9,10)
0,75 đ
TDLL
(TL 16b)
1 đ
TDLL
GTTH




17,5%
4
Định lí Thalès trong 
tam giác
(8t = 14,9%)
Định lí Thalès trong tam giác.

1
(TL 16a)
1 đ
TDLL
GQVĐ
2
(TN 11,12)
0,5 đ

TDLL
1
(TL16c)
1 đ
TDLL
GQVĐ


25%
5
Thu thập và tổ chức 
dữ liệu.
(10t =18,5 %)
Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ.





1
(TL 15)
1 đ
TDLL
MH


10%

9

9

2

1

21
Tỉ lệ phần trăm
30%
40%
20%
10%
100
Tỉ lệ chung
70%
30%
100

BẢNG ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I. NĂM HỌC 2023 - 2024
MÔN: TOÁN - LỚP: 8 – THỜI GIAN LÀM BÀI: 60 phút
TT
Chủ đề
Đơn vị kiến thức
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
NB
TH
VD
VDC
SỐ VÀ ĐẠI SỐ
1
Đa thức
Đa thức nhiều biến. Các phép toán cộng, trừ, nhân, chia các đa thức nhiều biến.
Nhận biết:
– Nhận biết được các khái niệm về đơn thức, đa thức nhiều biến, đơn thức đồng dạng, bậc của đa thức.
Thông hiểu: 
 – Tính được giá trị của đa thức khi biết giá trị của các biến.
 – Thực hiện được phép chia hết một đa thức cho một đơn thức trong những trường hợp đơn giản.
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức và phép chia hết một đơn thức cho một đơn thức.
– Thực hiện được các phép tính: phép cộng, phép trừ, phép nhân các đa thức nhiều biến trong những trường hợp đơn giản.

3
(TN1,2,3)

2 
(TL13a)
(TL13b)
2
Hằng đẳng thức đáng nhớ.
Hằng đẳng thức đáng nhớ.
Nhận biết:
– Nhận biết được các khái niệm: đồng nhất thức, hằng đẳng thức.
Thông hiểu:
– Mô tả được các hằng đẳng thức: bình phương của tổng và hiệu; hiệu hai bình phương; lập phương của tổng và hiệu; tổng và hiệu hai lập phương.
- Phân tích được đa thức thành nhân tử bằng cách đặt nhân tử chung trong trường hợp đơn giản.
– Vận dụng được các hằng đẳng thức để phân tích đa thức thành nhân tử ở dạng: vận dụng trực tiếp hằng đẳng thức;
– Vận dụng hằng đẳng thức thông qua nhóm hạng tử và đặt nhân tử chung.
2
(TN4,5)
2
(TN 6, 7 
2
(TL 14a)
(TL 14b)

1
(TL 17)
HÌNH HỌC PHẲNG
3
Tứ giác
Tính chất và dấu hiệu nhận biết các tứ giác đặc biệt.
Nhận biết: 
– Mô tả được tứ giác, tứ giác lồi.
– Giải thích được định lí về tổng các góc trong một tứ giác lồi bằng 360o.
– Nhận biết được dấu hiệu để một tứ giác là hình bình hành
– Nhận biết được dấu hiệu để một hình bình hành là hình chữ nhật 
– Nhận biết được dấu hiệu để một hình bình hành là hình thoi 
– Nhận biết được dấu hiệu để một hình chữ nhật là hình vuông 
Thông hiểu: – Hiểu được tứ giác là hình bình hành (ví dụ: tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành).
1
(TN 8)
1
(TN 9)
1
(TN 10)
1
(TL 16b)



4
Định lí Thalès trong tam giác
Định lí Thalès trong tam giác
Nhận biết: 
– Nhận biết được định nghĩa đường trung bình của tam giác. 
Thông hiểu
- Giải thích được tính chất đường trung bình của tam giác (đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó). 
– Giải thích được định lí Thalès trong tam giác (định lí thuận và đảo). 
– Giải thích được tính chất đường phân giác trong của tam giác. 
Vận dụng:
. Vận dụng tính chất đường phân giác trong của tam giác vào giải bài tập 
1
(TL16a)

 2
(TN11)
(TN12)
1
(TL16c)

MỘT SỐ YẾU TỐ THỐNG KÊ
5
Thu thập và tổ chức dữ liệu
Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ.
Vận dụng:
 – Lựa chọn và biểu diễn được dữ liệu vào bảng, biểu đồ thích hợp ở dạng: bảng thống kê; biểu đồ tranh; biểu đồ dạng cột/cột kép (column chart), biểu đồ hình quạt tròn (cho sẵn) (pie chart); biểu đồ đoạn thẳng (line graph).
– So sánh được các dạng biểu diễn khác nhau cho một tập dữ liệu.



1
(TL 15)

Tổng

9
9
2
1
Tỉ lệ %

30%
40%
20%
10%
Tỉ lệ chung

70%
30%

Phòng GD&ĐT Đại Lộc
Trường: TH và THCS Đại Chánh
Họ và tên:
Lớp:8/SBD:..
ĐỀ KIỂM TRA HỌC KỲ I
 Năm học: 2023 – 2024
MÔN: TOÁN 8
Thời gian: 60 phút (Không kể thời gian giao đề)
Ngày kiểm tra:.
ĐIỂM
NHẬN XÉT CỦA GIÁO VIÊN
A. PHẦN TRẮC NGHIỆM: (3 điểm) 
Mỗi câu sau đây có 4 lựa chọn, trong đó chỉ có một phương án đúng. Hãy khoanh tròn vào phương án mà em cho là đúng.
Câu 1. Có bao nhiêu đơn thức trong các biểu thức 3x; 4; x + y; x – y?
	A. 2.	B. 3.	C. 4.	D. 5.
Câu 2. Đơn thức đồng dạng với đơn thức 2y3 là
	A. –y2.	B. 3y3.	C. -3y.	D. y6.
Câu 3. Thương của phép chia (12x4y + 4x3 + 8x2y2) : (4x2) bằng
	A. 3x2y + x +2y2.	B. 3x4y + x3 – 2x2y2.
	C. -12x2y + 4x – 2y2.	D. 3x2y – x + 2y2.
Câu 4. Chọn câu SAI?
	A. (x + y)2 = (x + y) (x + y).	B. x2 – y2 = (x + y) (x – y).
	C. (-x – y)2 = (-x)2 – 2(-x)y + y2.	D. (x + y) (x + y) = y2 – x2.
Câu 5. Khai triển 9x2 – 25y2 theo hằng đẳng thức ta được
	A. (3x – 5y) (3x + 5y).	B. (3x – 25y) (3x + 25y).
	C. (2x – 5y) (2x + 5y).	D. (3x – 5y)2
Câu 6. Biểu thức 25x2 – 30xy + 9y2 bằng 
	A. (5x - 3y)2.	B. (3x – 5y)2.	C. (25x – 3y)2. 	D. (5x + 3y)2.
Câu 7. Hằng đẳng thức lập phương của một tổng là
	A. (A – B)3 = A3 – 3A2B + 3AB2 – B3.	B. (A + B)3 = A3 + 3A2B + 3AB2 + B3.
	C. (A + B)3 = A3 + 3A2B + 3AB – B3.	D. (A + B)3 = A2 + 3A2B + 3AB2 + B2.
Câu 8. Hình bình hành có một góc vuông là
	A. hình thoi.	B. hình thang cân.	
	C. hình chữ nhật.	D. hình vuông.
Câu 9. Tứ giác ABCD có số đo các góc A=100°; B=120°; D=80°. Số đo góc C bằng
	A. 50°.	B. 80°.	C. 110°.	D. 60°.
Câu 10. Điền từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo  là hình thoi”
	A. bằng nhau              
	B. giao nhau tại trung điểm mỗi đường và vuông góc với nhau
	C. giao nhau tại trung điểm mỗi đường
	D. bằng nhau và giao nhau tại trung điểm mỗi đường
Câu 11. Tam giác ABC có BC = 8cm. Gọi M, N lần lượt là trung điểm của AB và AC. Độ dài MN là
	A. 2 cm. B. 16 cm. C. 8 cm. D. 4 cm.
Câu 12. Cho hình vẽ, trong đó DE // BC, AD = 3, DB = 6
 AE = 4. Độ dài EC bằng
	A. 4. B.10	
	C. 6. D. 8.
B. PHẦN TỰ LUẬN: (7 điểm)
Câu 13: (1 điểm): Cho biểu thức P = x(x2 – y) – x2(x +y) + xy(x – 2).
a) Rút gọn biểu thức P.
b) Tính giá trị của P khi x = 2, y = -3.
Câu 14: (1 điểm ): Phân tích đa thức thành nhân tử:	
a) x2 – 2x.
b) x2 – 6x + 9 – y2.
Câu 15: (1 điểm): Bảng sau cho biết số lượng pin cũ thu được của các lớp khối 8:
Lớp
8A
8B
8C
8D
Số lượng pin
165
200
180
170
Lựa chọn biểu đồ phù hợp biểu diễn bảng thống kê trên. Vẽ biểu đồ đó.
Câu 16: (3 điểm): Cho △ABC, M trung điểm AB, vẽ MN //BC tại N.
a) Chứng minh MN là đường trung bình của △ABC.
b) Tia phân giác của góc A cắt BC tại I. Vẽ điểm K sao cho N là trung điểm của IK. Tứ giác AICK là hình gì? Vì sao?
c) Chứng minh IB . NC = IC . MB.
Câu 17: (1 điểm): Cho a + b = 1, tính giá trị biểu thức sau:
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b).
ĐÁP ÁN VÀ BIỂU ĐIỂM ĐỀ KIỂM TRA HỌC KÌ 1-TOÁN 8
A. TRẮC NGHIỆM: (3 điểm): Mỗi câu đúng: 0,25đ
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đ/án
A
B
A
D
A
A
B
C
D
B
D
D
B. TỰ LUẬN: (7 điểm)
Bài
Nội dung
Điểm
Câu 13
1đ
a) P = x(x2 – y) – x2(x +y) + xy(x – 2)
P = x3 – xy – x3 – x2y + x2y – 2xy
P = (x3 – x3) + (-x2y + x2y) + (-xy – 2xy)
P = -3xy

0,25
0,25
b) Thay x = 2, y = -3 vào P = -3xy
Ta được P = -3 . 2 . (-3) = 18
Vậy khi x = 2, y = -3 thì P = 18

0,25
0,25
Câu 14
1đ
a) x2 – 2x = x(x – 2)
0,5
b) x2 – 2x + 4 – y2
= (x – 2)2 – y2
= (x – 2 – y) (x – 2 + y)

0,25
0,25
Câu 15
1đ
Chọn đúng loại biểu đồ và biểu diễn được các trục của biểu đồ.
Thể hiện đúng số lượng pin của mỗi lớp trên biểu đồ.
0,25
0,75
Câu 16
3đ

Vẽ hình câu a: 0,25
Câu b: 0,25
a) Xét △ABC có M trung điểm AB và MN // BC (gt)
⇒ N trung điểm AC.
Ta có M trung điểm AB, N trung điểm AC 
nên MN là đường trung bình của △ABC (đ/n)

0,25
0,25
b) Xét tứ giác AICK có N là trung điểm AC (cmt) 
và N trung điểm IK (gt) 
nên tứ giác AICK là hình bình hành.

0,5
0,5
c) Ta có AI là tia phân giác của góc BAC 
nên IBIC=ABAC (1)
Mà AB = 2 MB (M trung điểm AB (gt)) (2)
AC = 2NC ( N trung điểm AC (cmt)) (3)
Từ (1), (2), (3) suy ra IBIC=MBNC hay IB . NC = IC . MB

0,5
0,5
Câu 17
1đ
M = (a + b)3 – 3a2b – 3ab2 + 3ab[(a + b)2 -2ab] + 6a2b2(a + b)
= 1 – 3ab (a + b) + 3ab(1 – 2ab) + 6a2b2
= 1 – 3ab + 3ab – 6a2b2 + 6a2b2 = 1

0,5
0,5
Học sinh giải cách khác đúng vẫn ghi điểm tối đa.