Đề kiểm tra học kì II môn Toán Lớp 7 - Năm học 2010-2011

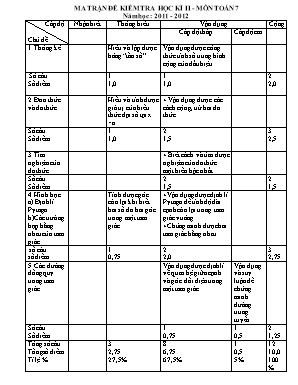
 MA TRẬN ĐỀ KIỂM TRA HỌC KÌ II - MÔN TOÁN 7
Năm học : 2011 - 2012
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độcao
1. Thống kê
Hiểu và lập được bảng “tần số”
Vận dụng được công thức tính số trung bình cộng của dấu hiệu
 Số câu
Số điểm
1
1,0
1
1,0
2
2,0
2. Đơn thức và đa thức
Hiểu và tính được giá trị của biểu thức đại số tại x =a
+ Vận dụng được các cách cộng, trừ hai đa thức
Số câu
Số điểm
1
1,0
2
1,5
3
2,5
3. Tìm nghiệm của đa thức
+ Biết cách và tìm được nghiệm của đa thức một biến bậc nhất.
Số câu
Số điểm
2
1,5
2
1,5
4. Hình học.
a) Định lí Pytago 
b)Các trường hợp bằng nhau của tam giác
Tính được góc còn lại khi biết hai số đo hai góc trong một tam giác
+Vận dụng được định lí Pytago đế tính độ dài cạnh còn lại trong tam giác vuông
+Chứng minh được hai tam giác bằng nhau
 số câu
số điểm
1
0,75
2
2,0
3
2,75
5. Các đường đồng quy trong tam giác
Vận dụng được định lí về quan hệ giữa cạnh và góc đối diện trong một tam giác
Vận dụng và suy luận để chứng minh đường trung tuyến
Số câu
Số điểm
1
0,75
1
0,5
2
1,25
Tổng số câu
Tổngsố điểm
Tỉ lệ %
3
2,75
27,5%
8
6,75
67,5%
1
0,5
5%
12
10,0
100%
PHÒNG GIÁO DUC - ĐÀO TẠO TP.PLEIKU
TRƯỜNG TH - THCS NGUYỄN CHÍ THANH
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA HỌC KÌ II - MÔN TOÁN 7
NĂM HỌC : 2010 - 2011
 Thời gian: 90 phút ( Không kể phát đề)
 Mã đề: 
Bài 1. (2đ). Năng suất lúa đông xuân (tính theo tạ / ha ) của 20 hợp tác xã được ghi lại trong bảng sau:
45 45 40 40 35 40 30 45 35 40
35 40 35 45 45 35 45 40 30 40
a) Lập bảng “tần số”
b) Tính số trung bình cộng và tìm Mốt của dấu hiệu
Bài 2. (1đ) Tính giá trị của đa thức P(x) = 5x2 – 4x – 4. tại x = - 2
Bài 3. (1,5đ) Cho các đa thức A(x)= 5x3 – 4x2 – 3x + 2 ; B(x) = x3 + 3x2 – 4x – 4
a) Tính A(x) + B(x) 
b) Tìm đa thức C(x) sao cho C(x) + A(x) = B(x) 
Bài 4. (1,5đ). Tìm nghiệm của các đa thức sau: 
 a) 24 + 4x b) 
Bài 5. (1,5đ) Cho có .
 a) Tính số đo góc C
 b) So sánh các cạnh của 
Bài 6. (2,5đ) Cho ∆ABC vuông tại A có cạnh AB = 8cm, cạnh AC = 6cm . Trên cạnh AB lấy điểm D sao cho AD = AC ( D nằm giữa A; B). Trên tia đối của tia CA lấy điểm E sao cho AE = AB ( C nằm giữa A; E). Kẻ AH là đường cao của ∆ABC. Đường thẳng AH cắt DE tại M ( M nằm giữa D; E )
a) Tính độ dài cạnh BC
b) Chứng minh ∆ABC = ∆AED
c) Chứng minh AM là trung tuyến của ∆ADE
............. Hết ............................
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
NỘI DUNG
Điểm
Bài 1. (2 đ) . 
a) Lập bảng “tần số”
Giá trị (x)
30
35
40
45
Tần số (n)
2
5
7
6
N = 20
b) Số trung bình cộng của dấu hiệu
 .......................................................
 Mốt của dấu hiệu M0 = 7 ....................................................................
Bài 2. (1đ) Thay x = -2 . 
Ta có P(-2) = 5 .(-2)2 – 4.(-2) – 4 ......................................................................
 = 5. 4 + 8 – 4 = 20 + 8 - 4 = 24 . (0,5đ) .............................................
Vậy giá trị của đa thức P(x) = 5x2 – 4x – 4 tại x = -2 là 24 ..................................
Bài 3 (1,5đ) 
a) Tính được : A(x) +B(x) = 6x3 – x2 – 7x - 2 . .........................................................
 * (Nếu sai một hạng tử trừ 0,25đ)
b) Ta có C(x) + A(x) = B(x) ;Suy ra : C(x) = B(x) – A(x) ..................................
 Tính được : B(x) – A(x) = - 4x3 + 7x2 – 4x – 6 ................................
 *(Nếu sai một hạng tử trừ 0,25đ)
Bài 4. (2 đ). a) 24 + 4x = 0 ; 
 4x = -24 .................................................................. 
 x = (-24) : 4 = - 6 ..................................................................
 b) = 0 ; 
 .................................................................. 
 x = ...............................................................
Bài 5. (1,5đ). a) Ta có ( Tổng ba góc trong tam giác) .....................
 Hay .................................................................
 Suy ra ........................................
 b) Xét ∆ABC . Ta có ..................
 Suy ra AB < BC < AC ( Quan hệ giữa cạnh và góc đối diện trong một tam giác)
Bài 4 (3 đ). Hình vẽ (0,25 đ)
∆ABC vuông tại A, theo định lí Pytago, ta có:
 BC2 = AB2 + AC2 ............................................................................. 
 = 82 + 62 = 100 ...............................................................................
Suy ra BC = = 10 (cm) ........................................................................... 
Xét ∆ABC và ∆AED, ta có 
AB = AE (GT) .......................................................................................
Góc A là góc chung ..................................................................................... 
AD = AC (GT) ...................................................................................
Vậy ∆ABC = ∆AED ( c- g - c) .......................................................................
c) Ta có (vì ∆ABH vuông tại H )
 (vì ∆ABC vuông tại A)
 suy ra 
 Lại có ( vì ∆ABC = ∆AED ở câu a )
 Nên . 
Do đó ∆AME cân tại M. Suy ra MA = ME (1) ...........................................
 Ta có (vì ∆ACH vuông tại H )
 (vì ∆ABC vuông tại A)
 suy ra 
Lại có ( vì ∆ABC = ∆AED ở câu a )
 Nên . 
Do đó ∆AMD cân tại M. Suy ra MA = MD (2) .........................................
Từ (1) và (2) suy ra MD = ME . 
Vậy AM là trung tuyến của ∆ADE ............................................................
 *(HS làm theo cách khác đúng vẫn cho điểm tối đa)
1,0
0,75
0,25
0,25
0,5
0,25
0,75
0,25
0,5
0,25
0,5
0,25
0,5
0,25
0,25
0,25
0,25
0,5
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25