Đề kiểm tra học kì II lớp 10 năm học: 2013 – 2014 môn: Toán. Thời gian làm bài: 90 phút (không kể thời gian phát, chép đề)

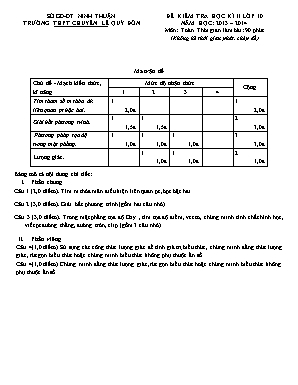
SỞ GD-ĐT NINH THUẬN
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN
ĐỀ KIỂM TRA HỌC KÌ II LỚP 10
NĂM HỌC: 2013 – 2014
Môn: Toán. Thời gian làm bài: 90 phút
(Không kể thời gian phát, chép đề)
Ma trận đề
Chủ đề - Mạch kiến thức, kĩ năng
Mức độ nhận thức
Cộng
1
2
3
4
Tìm tham số m thỏa đk liên quan pt bậc hai.
1
2,0đ
1
2,0đ
Giải bất phương trình.
1
1,5đ
1
1,5đ
2
3,0đ
 Phương pháp tọa độ trong mặt phẳng.
1
1,0đ
1
1,0đ
1
1,0đ
3
3,0đ
Lượng giác.
1
1,0đ
1
1,0đ
2
1,0đ
Bảng mô tả nội dung chi tiết:
Phần chung
Câu 1 (2,0 điểm). Tìm m thỏa mãn điều kiện liên quan pt ,bpt bậc hai. 
Câu 2 (3,0 điểm). Giải bất phương trình (gồm hai câu nhỏ) 
Câu 3 (3,0 điểm). Trong mặt phẳng tọa độ Oxy , tìm tọa độ điểm, vecto, chứng minh tính chất hình học, viết pt đường thẳng, đường tròn, elip (gồm 3 câu nhỏ).
Phần riêng
Câu 4(1,0 điểm) Sử sụng các công thức lượng giác để tính giá trị biểu thức, chứng minh đẳng thức lượng giác, rút gọn biểu thức hoặc chứng minh biểu thức không phụ thuộc ẩn số.
Câu 4(1,0 điểm) Chứng minh đẳng thức lượng giác, rút gọn biểu thức hoặc chứng minh biểu thức không phụ thuộc ẩn số.
SỞ GD – ĐT NINH THUẬN
ĐỀ KIỂM TRA HỌC KỲ II NĂM 2013 - 2014
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN
MÔN TOÁN – KHỐI 10
THỜI GIAN : 90 PHÚT
PHẦN CHUNG (8,0 điểm)
Câu 1 (2,0 điểm). Tìm để phương trình vô nghiệm. 
Câu 2 (3,0 điểm). Giải bất phương trình sau : 
Câu 3 (3,0 điểm). Trong mặt phẳng tọa độ Oxy cho hai điểm và.
a) Chứng minh rằng tam giác OAB vuông tại O;
b) Tính độ dài và viết phương trình đường cao OH của tam giác OAB;
c) Viết phương trình đường tròn ngoại tiếp tam giác OAB.
PHẦN RIÊNG (2,0 điểm) 
(Học sinh học theo chương trình nào thì chỉ được làm phần dành cho chương trình đó)
DÀNH CHO CHƯƠNG TRÌNH CHUẨN (10L, 10H, 10V, 10TA)
Câu 4a (1,0 điểm). Tính giá trị của biểu thức .
Câu 5a (1,0 điểm). Chứng minh .
DÀNH CHO CHƯƠNG TRÌNH NÂNG CAO (10A1, 10A2)
Câu 4b (1,0 điểm). Cho . Tính .
Câu 5b (1,0 điểm). Chứng minh rằng nếu thì tam giác ABC vuông ở A.
DÀNH CHO CHƯƠNG TRÌNH CHUYÊN (10T)
Câu 4c (1,0 điểm). Chứng minh .
Câu 5c (1,0 điểm). Chứng minh rằng trong mọi tam giác ABC ta đều có : 
 .
------- HẾT -------
(Giám thị không giải thích gì thêm)
ĐÁP ÁN, HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
CÂU
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
ĐIỂM
Câu 1
(2,0 điểm)
Phương trình vô nghiệm 
1,00 đ
0,50 đ
 hoặc 
0,50đ
Câu 2.a
(1,5 điểm)
0,5đ
0,5đ
Vậy nghiệm 
0,5đ
Câu 2.b (1,5 điểm)
0,5đ
0,5đ
Vậy tập nghiệm của bất phương trình là 
0,5đ
Câu 3.a
(1,0điểm)
0,5đ
. Vậy tam giác OAB vuông tại O.
0,5đ
Câu 3.b
(1,0điểm)
0,25đ
Do tam giác OAB vuông tại O nên ta có:
OH.AB = OA.OB 
0,25đ
Đường cao OH đi qua O(0;0) và nhận làm vectơ pháp tuyến
0,25đ
(x – 0) - (y – 0) = 0 2x – 9y = 0
0,25đ
Câu 3.c
(1,0điểm)
Do tam giác OAB vuông tại O, nên tâm của đường tròn ngoại tiếp tam giác OAB là trung điểm I của cạnh AB.
 Bán kính đường tròn ngoại tiếp tam giác OAB là: 
0,5đ
Vậy phương trình đường tròn ngoại tiếp tam giác OAB là:
0,5đ
Câu 4a
(1,0điểm)
0,25đ
0,25đ
0,25đ
.
0,25đ
Câu 5a
(1,0 điểm)
0,25đ
0,25đ
0,5đ
Câu 4b
(1,0điểm)
0,25đ
0,25đ
0,25đ
0,25đ
Câu 5b
(1,0 điểm)
Gt 
0,25đ
0,25đ
0,25đ
 hay tam giac ABC vuông tại A.
0,25đ
Câu 4c
(1,0 điểm)
0,25đ
Ta có: 
0,25đ
0,25đ
 và . Từ đó . Suy ra đẳng thức cần chứng minh.
0,25đ
Câu 5c
(1,0 điểm)
Ta có : Vế trái = sinA + sinB - sinC 
 = - sinC.
 = 
0,25đ
 = 
 =
0,25đ
 = 
0,25đ
= = vế phải.(đpcm).
0,25đ
------- HẾT -------
LƯU Ý KHI CHẤM BÀI: Điểm bài kiểm tra được làm tròn đến 1 chữ số thập phân, học sinh có cách giải đúng khác với đáp án vẫn được điểm tối đa của phần đó.