Đề kiểm tra cuối học kỳ II môn Toán Lớp 8 (Kết nối tri thức và cuộc sống) - Năm học 2023-2024 - Trường THCS Võ Thị Sáu (Có đáp án)

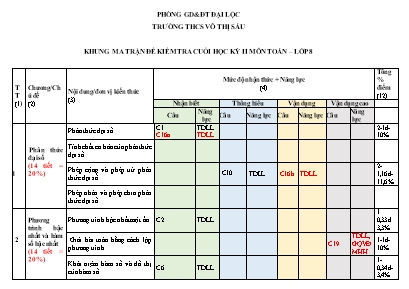
PHÒNG GD&ĐT ĐẠI LỘC
TRƯỜNG THCS VÕ THỊ SÁU
KHUNG MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KỲ II MÔN TOÁN – LỚP 8
TT
(1)
Chương/Chủ đề
(2)
Nội dung/đơn vị kiến thức
(3)
Mức độ nhận thức + Năng lực
(4)
Tổng % điểm
(12)
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao

Câu
Năng lực
Câu
Năng lực
Câu
Năng lực
Câu
Năng lực


1
 Phân thức đại số
(14 tiết = 20%)

Phân thức đại số
C1
C16a
TDLL
TDLL






2-1đ-10%
Tính chất cơ bản của phân thức đại số

Phép cộng và phép trừ phân thức đại số


C10
TDLL
C16b
TDLL


2-1,16đ-11,6%
Phép nhân và phép chia phân thức đại số









2

Phương trình bậc nhất và hàm số bậc nhất
(14 tiết = 20%)

Phương trình bậc nhất một ẩn
C2
TDLL






1
0,33d
3,3%
 Giải bài toán bằng cách lập phương trình






C19
TDLL,GQVĐMHH
1-1đ-10%
Khái niệm hàm số và đồ thị của hàm số
C6
TDLL






1-0,34đ-3,4%
Hàm số bậc nhất và đồ thị của hàm số bậc nhất


17a
TDLL




1-1đ-10%
Hệ số góc của đường thẳng
C3
C5
TDLL
TDLL
17b
TDLL




3
1,17đ
11,7%
 3
Mở đầu về tính xác suất của biến cố
(7 tiết = 10%)
 
Kết quả có thể và kết quả thuận lợi
C4
TDLL






1
0,34d
3,4%
Cách tính xác suất của biến cố bằng tỉ số









Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng




C7
TDLL,GQVĐMHH


1
0,33đ
3,3%
4
Tam giác đồng dạng
 (14 tiết = 20%)

Hai tam giác đồng dạng


C15
TDLL




1
0,33đ
3,3%
Ba trường hợp đồng dạng của hai tam giác
C11
TDLL






1
0,34đ
3,4%
Định lí Pythagore và ứng dụng


C12
TDLL
C18b
TDLL


2
0,57đ-5,7%
Các trường hợp đồng dạng của hai tam giác vuông


C18a
TDLL
C18b
TDLL


2
0,75đ
7,5%
Hình đồng dạng
C8
TDLL,MHH






1
0,34đ
3,4%

5
Một số hình khối trong thực tiễn
(6 tiết = 9%)
Một số hình khối trong thực tiễn (hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng)









Hình chóp tam giác đều
C14







1
0,33đ
3,3%
Hình chóp tứ giác đều

C13



C9
TDLL,MHH,GGQVĐ


2
0,67đ
6,7%
Tổng số câu









Tỉ lệ %
40%
30%
20%
10%
100%
Tỉ lệ chung
70%
30%
100%

BẢNG ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KỲ II MÔN TOÁN – LỚP 8
TT
Chương/
Chủ đề
Nội dung/Đơn vị kiến thức
Mức độ đánh giá 
Số câu hỏi theo mức độ nhận thức
Nhận 
Biết
Thông hiểu
Vận dụng
Vận dụng cao

1
 Phân thức đại số
(14 tiết = 20%)

Phân thức đại số
- HS nhận biết được khái niệm phân thức đại số
-Nhận biết điều kiện xác định của phân thức đại số
1TN,1TL
(C1, C16a)

Tính chất cơ bản của phân thức đại số



Phép cộng và phép trừ phân thức đại số
Thực hiện phép cộng các phân thức đại số

1TN
(C10)

1TL
(C16b)


Phép nhân và phép chia phân thức đại số





2
Phương trình bậc nhất và hàm số bậc nhất
(14 tiết = 20%)

Phương trình bậc nhất một ẩn
Nhận biết được phương trình bậc nhất một ẩn
1TN
(C2)



 Giải bài toán bằng cách lập phương trình
Giải quyết vấn đề thực tiễn gắn với phương trình bậc nhất



1 TL
(C19)
Khái niệm hàm số và đồ thị của hàm số
Nhận biết đồ thị của hàm số
1 TN
(C6)



Hàm số bậc nhất và đồ thị của hàm số bậc nhất
-Vận dụng vẽ đồ thị hàm số bậc nhất
1 TL
17a



Hệ số góc của đường thẳng
-Nhận biết được hệ số góc của đường thẳng y = ax + b (a ≠0)
-Sử dụng hệ số góc để nhận biết hai đường thẳng cắt nhau, giải thích hai đường thẳng song song.
2TN, 1TL
(C3,C5
17b)




3

Mở đầu về tính xác suất của biến cố
(7 tiết = 10%)
 
Kết quả có thể và kết quả thuận lợi

1TN
(C4)



Cách tính xác suất của biến cố bằng tỉ số





Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng
Tính xác suất thực nghiệm


1TN
(C7)

4
Tam giác đồng dạng
 (14 tiết = 20%)

Hai tam giác đồng dạng
Hiểu được tỉ số đồng dạng của hai tam giác đồng dạng


1TN
(C15)


Ba trường hợp đồng dạng của hai tam giác
Nhận biết trường hợp đồng dạng của hai tam giác
1TN
(C11)



Định lí Pythagore và ứng dụng
-Hiểu được định lí Pythagore
-Tính được độ dài cạnh của tam giác vuông bằng định lí Pythagore

1TN
(C12)
1TL
(C18b)

Các trường hợp đồng dạng của hai tam giác vuông
Giải thích các trường hợp đồng dạng của hai tam giác vuông

1TL
(C18a)
1TL
(C18b)

Hình đồng dạng
Nhận biết hai hình đồng dạng

1TN
(C8)



5
Một số hình khối trong thực tiễn
(6 tiết = 9%)
Một số hình khối trong thực tiễn (hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng)







Hình chóp tam giác đều

- Mô tả đỉnh, cạnh bên, mặt bên, mặt đáy của hình chóp tam giác đều
1TN
(C14)




Hình chóp tứ giác đều

- Mô tả đỉnh, cạnh bên, mặt bên, mặt đáy của hình chóp tứ giác đều
1TN
(C13)

1TN
(C9)

Tổng số câu

13
4
5
1
Tỉ lệ %

40
30
20
10
Tỉ lệ chung

70
30

ĐỀ KIỂM TRA CUỐI HỌC KỲ II – TOÁN 8
I. TRẮC NGHIỆM KHÁCH QUAN (5,0 điểm)
Câu 1: Cách viết nào sau đây là không phải là phân thức đại số ? 
A. x-1x+3	 B. x	 C. x-11x	 D. -7
Câu 2: Phương trình nào sau đây là phương trình bậc nhất một ẩn?
A. 2x+4=0 B. x2-1=0	C. 0x-5=0	 D. x3=8
Câu 3: Hệ số góc của đường thẳng y = 3x +2 là
A. 3	 B. 2	 C.32	 D. -3
Câu 4: Kết quả có thể khi gieo một con xúc xắc là
A. 0 chấm	 B. 8 chấm	 C. 4 chấm	 D. 7 chấm	
Câu 5: Đồ thị hàm số y = 3x + 2 cắt đồ thị hàm số nào sau đây?
A. y = x + 1	 B.y= 3x +1	 C.y = 3x + 3 D. y = 3x 
Câu 6: Đồ thị hàm số y = 2x +3 đi qua điểm nào sau đây?
A. (0;2)	 B.(3;0)	 	C.(0;0) 	 D. (-1;1) 
Câu 7: Bảng sau thống kê điểm tra cuối kỳ I môn Toán của 100 học sinh lớp 8 được chọn ngẫu nhiên tại ba lớp của một trường Trung học cơ sở:
Điểm
1
2
3
4
5
6
7
8
9
10
Số học sinh
5
6
11
12
11
12
18
9
8
8
Gặp ngẫu nhiên một học sinh lớp 8 của trường đó. Xác xuất thực nghiệm của biến cố ”Học sinh đó được trên 8 điểm Toán” là
A. 0,34	B. 0,66	C. 0,16 	D. 0,45
Câu 8: Tìm hình đồng dạng với hình bên
A

B

C

D

Câu 9: Một chiếc lều có dạng hình chóp tứ giác đều, cạnh đáy bằng 3 m, chiều cao bằng 2 m. Biết lều phủ bạt bốn phía và cả mặt tiếp đất. Thể tích không khí trong lều là bao nhiêu?
A. .	B. .	C. .	D. .
Câu 10: Kết quả của phép tính 4x+3x là
A. 1x	B. 7x	C. 72x	D. 12x
Câu 11: D ABC và D DEF có: A=E, C=F , kết luận nào sau đây đúng:
A. D ABC DDEF; 	 B. DABC D EDF; 
C. DABC DEFD ; 	 D. DABC DFDE
Câu 12: Cho ∆ ABC vuông tại A. Phát biểu nào sau đây đúng với nội dung định lí Phythagore?
A. AB2=AC2+BC2 	 B. AB2=AB2+BC2 
 C.BC2=AC2-AB2	 D. BC2=AB2+AC2
Câu 13: Số mặt bên của hình chóp tứ giác đều là
A.4	B.3	C.5	D.6
Câu 14: Mặt bên của hình chóp tam giác đều là một
A.tam giác cân	B. tam giác đều	C. hình chữ nhật	D. hình vuông
Câu 15: DABC DDEF theo hệ số tỉ lệ k thì DDEF DABC theo hệ số tỉ lệ là:
A. k	 B. 	 C. k2	 D. 
II TỰ LUẬN ( 5 điểm )
Câu 16: (1,5 đ) Cho hai phân thức 1x+1 và 2x-1 
a.Tìm điều kiện xác định của hai phân thức trên. (0,67đ) NB
b.Thu gọn: 1x+1 + 2x-1 VD (0,83 đ)
Câu 17: (1,5đ)
a.Vẽ đồ thị hàm số y = -x + 2 (1 đ) TH 
b.Tìm giá trị của tham số m để đồ thị hàm số y = (m+1)x - 3 song song với đồ thị hàm số 
y = - x + 2. (0,5 đ) TH 
Câu 18: (1đ) Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8m. Đường cao AH (H∈BC)
 a/Chứng minh : ∆ABC ∆HBA (0,5 đ) TH
 b/ Tính BC, AH. (0,5 đ) VD 
Câu 19: (1đ )VDC
Tuổi của ông hơn tuổi của cháu 56 tuổi, cách đây 5 năm tuổi của ông gấp 8 lần tuổi của cháu. Hỏi tuổi của cháu hiện nay bao nhiêu tuổi? 
HƯỚNG DẪN CHẤM
I . TRẮC NGHIỆM . ( 5 ĐIỂM ) ( Mỗi câu đúng 0.33 điểm )
Câu 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Đáp án
C
A
A
C
A
D
C
B
C
B
B
D
A
A
B

II . TỰ LUẬN . ( 5 ĐIỂM )
Câu 16. (1,5 đ)Cho hai phân thức 1x+1 và 1x-1 
a.ĐKXĐ: x ≠1; x ≠-1 (Đúng mỗi đk đc 0,33đ)
b. 1x+1 + 1x-1 = x-1(x+1)(x-1)+x+1(x+1)(x-1) (0,5)đ
=2xx+1x-1 (0,2đ)
= 2xx2-1(0,13đ)
Câu 17: (1,5đ)
a.Lập bảng đúng (0,5 đ)
Vẽ đúng đồ thị hàm số y = -x + 2 (0,5 đ)
b. Để đồ thị hàm số y = (m+1)x - 3 song song với đồ thị hàm số y = - x + 2 thì m + 1 = -1 (0,25đ)
Tìm được m = -2 (0,25đ)
Câu 18: (1đ) a/Chứng minh : ∆ABC ∆HBA 
Nêu được 2 cặp góc bằng nhau của hai tam giác trên. (0,25đ)
Kết luận đúng (0,25đ)
b. -Áp dụng định lí Pythagore tính đúng BC = 10 cm (0,25đ)
-∆ABC ∆HBA => ACAH=BCAB => AH = AC.ABBC (0,15 đ)
Thế số tính được AH = 4,8 cm (0,1 đ)
Câu 19: (1đ )
Gọi tuổi của cháu hiện nay là x (tuổi) ( x ∈N*) 
Suy ra tuổi của ông hiện nay là x + 56 (tuổi)(0,25đ)
Tuổi của cháu cách đây 5 năm là x – 5 (tuổi)
Tuổi của ông cách đây 5 năm là x +56 – 5= x +51 (tuổi) (0,25 đ)
Cách đây 5 năm tuổi của ông gấp 8 lần tuổi của cháu nên ta có phương trình:
 x+51 = 8.(x-5) (0,25 đ)
Giải phương trình trên ta được x = 13 (TMĐK)
Vậy tuổi của cháu hiện nay là 13 tuổi. (0,25 đ)