Đề kiểm tra chương III (năm học 2015 - 2016) môn: Hình học 9 thời gian: 45 phút

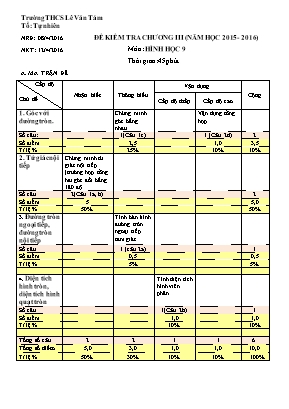
Trường THCS Lê Văn Tám
Tổ: Tự nhiên
NRĐ: 08/4/2016 	 ĐỀ KIỂM TRA CHƯƠNG III (NĂM HỌC 2015 - 2016) 
NKT: 12/4/2016 Môn: HÌNH HỌC 9 
 Thời gian: 45 phút
A. MA TRẬN ĐỀ 
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Góc với đường tròn.
Chứng minh góc bằng nhau.
Vận dụng tổng hợp.
Số câu: 
1(Câu 1c)
1 (Câu 2d)
2
Số điểm 
2,5
1,0
3,5
Tỉ lệ %
25%
10%
10%
2. Tứ giác nội tiếp
Chứng minh tứ giác nội tiếp (trường hợp tổng hai góc đối bằng 180 độ.
Số câu 
2(Câu 1a, b)
2
Số điểm 
5
5,0
Tỉ lệ %
50%
50%
3. Đường tròn ngoại tiếp, đường tròn nội tiếp
Tính bán kính đường tròn ngoại tiếp tam giác.
Số câu 
1 (câu 2a)
1
Số điểm 
0,5
0,5
Tỉ lệ %
5%
5%
4. Diện tích hình tròn, diện tích hình quạt tròn
Tính diện tích hình viên phân.
Số câu 
1(Câu 2b)
1
Số điểm 
1,0
1,0
Tỉ lệ %
10%
10%
Tổng số câu 
2
2
1
1
 6
Tổng số điểm 
5,0
3,0
1,0
1,0
10,0
Tỉ lệ %
50%
30%
10%
10%
100%
B. NỘI DUNG ĐỀ
Trường THCS Lê Văn Tám 
Lớp:..................... 
 ĐỀ KIỂM TRA CHƯƠNG III (NĂM HỌC 2015 - 2016) 
 Môn: HÌNH HỌC 9 
 Thời gian: 45 phút
 Điểm:
 Nhận xét của giáo viên:
Bài 1 (8,0 điểm). Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm); AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B).
Chứng minh tứ giác AMCO nội tiếp đường tròn.
Chứng minh: tứ giác AMDE nội tiếp được.
 c) Chứng minh .
 d) Vẽ CH vuông góc với AB (H AB). Chứng minh rằng MB đi qua trung điểm của CH. 
Bài 2 (2,0 điểm). Cho đều có cạnh bằng nội tiếp đường tròn (O). 
Tính bán kính R của đường tròn (O).
Tính diện tích hình viên phân chắn cung nhỏ của (O) theo .
---------- Hết ----------
C. ĐÁP ÁN 
BÀI
CÂU
NỘI DUNG
ĐIỂM
1
a)
Vì MA, MC là tiếp tuyến nên: 
 AMCO là tứ giác nội tiếp đường tròn đường kính MO (vì có tổng hai góc đối bằng . 
0,5 x2 
0,5x2
0,25x2
b)
Ta có : (góc nội tiếp chắn nửa đường tròn)
 (1) 
 OA = OC = R, MA = MC (tính chất tiếp tuyến) 
 OM là đường trung trực của AC 
 (2)
Từ (1) và (2) D, E thuộc đường tròn đường kính ME
MADE là tứ giác nội tiếp đường tròn đường kính MA.
0,5
0,25
0,25
0,25
0,25
0,25
 0,25
c)
Tứ giác AMDE nội tiếp (g.n.t cùng chắn ) (3)
Tứ giác AMCO nộitiếp(g.n.t cùng chắn cung) (4) 
Từ (3) và (4) 
1,0
1,0
0,5
d)
 Tia BC cắt Ax tại N. Ta có (g.nt chắn nửa đường tròn)
 ∆ACN vuông tại C.
 Vì MC=MA nên MC = MN, do đó MA = MN (5)
 Ta có CH // NA (cùng vuông góc với AB)
 (định lí Ta-lét) (6)
Từ (5) và (6) suy ra IC = IH MB đi qua trung điểm của CH.
0,25
0,25
0,25
0,25
2
a)
Gọi R là bán kính của (O) và h là chiều cao của đều, ta có:
 h = 
 O là trọng tâm của R = OA = h =
0,25
0,25
b)
S(O) = R2 = (đvdt)
SABC = a.h = (đvdt)
Svp = ( S(O) – SABC ) = ( - ) = (đvdt)
0,25
0,25
0,5
****** HẾT ******
Tổ trưởng chuyên môn Giáo viên ra đề
 Trần Thị Mỹ Linh Nguyễn Tri Phương