Đề kiểm tra chất lượng giữa kì II môn toán – Khối 10

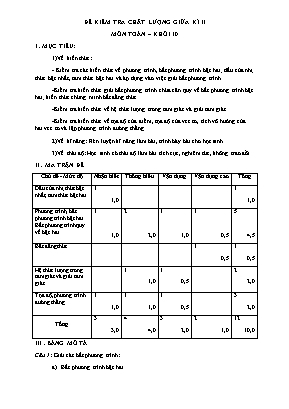
ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA KÌ II
MÔN TOÁN – KHỐI 10
I . MỤC TIÊU:
	1)Về kiến thức:
	- Kiểm tra các kiến thức về phương trình, bất phương trình bậc hai; dấu của nhị thức bậc nhất, tam thức bậc hai và áp dụng vào việc giải bất phương trình.
	-Kiểm tra kiến thức giải bất phương trình chứa căn quy về bất phương trình bậc hai; kiến thức chứng minh bất đẳng thức.
	-Kiểm tra kiến thức về hệ thức lượng trong tam giác và giải tam giác.
	-Kiểm tra kiến thức về tọa độ của điểm, tọa độ của vec tơ, tích vô hướng của hai vec tơ và lập phương trình đường thẳng.
	2)Về kĩ năng: Rèn luyện kĩ năng làm bài, trình bày bài cho học sinh.
	3)Về thái độ:	Học sinh có thái độ làm bài tích cực, nghiêm túc, không trao đổi.
II . MA TRẬN ĐỀ
Chủ đề - Mức độ
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
Tổng
Dấu của nhị thức bậc nhất, tam thức bậc hai
1
1,0
1
1,0
Phương trình, bất phương trình bậc hai. Bất phương trình quy về bậc hai.
1
1,0
2
2,0
1
1,0
1
0,5
5
4,5
Bất đẳng thức
1
0,5
1
0,5
Hệ thức lượng trong tam giác và giải tam giác
1
1,0
1
0,5
2
2,0
Tọa độ, phương trình đường thẳng
1
1,0
1
1,0
1
0,5
3
2,0
Tổng
3
3,0
4
4,0
3
2,0
2
1,0
12
10,0
III . BẢNG MÔ TẢ
Câu 1: Giải các bất phương trình:
Bất phương trình bậc hai
Bất phương trình chứa thương các nhị thức bậc nhất và tam thức bậc hai
Bất phương trình chứa căn dạng cơ bản.
Câu 2: Cho biểu thức chứa tham số m trong hệ số a.
Tìm m để phương trình có hai nghiệm phân biệt.
Tìm m để với 
Câu 3: Cho tam giác ABC có độ dài 3 cạnh là a, b, c
Cho biết độ dài hai cạnh a, c. Tính độ dài cạnh b và ma.
Chứng minh hệ thức trong tam giác.
Câu 4: Cho tam giác ABC với tọa độ A, B, C cho trước.
Lập phương trình tham số cạnh AB của tam giác ABC.
Lập phương trình đường trung tuyến đi qua đỉnh A của tam giác ABC.
Tìm tọa độ điểm D thuộc trục Oy sao cho tam giác ABD vuông tại A.
Câu 5: a) Giải bất phương trình chứa căn quy về bậc hai.
	b)Chứng minh bất đẳng thức.
IV . ĐỀ BÀI
Câu 1. (3 điểm) Giải các bất phương trình sau:
	b) 	 c) 
Câu 2. (2 điểm) Cho biểu thức 
Tìm các giá trị của m để phương trình có hai nghiệm phân biệt.
Tìm các giá trị của m để với 
Câu 3. (1,5 điểm) Cho tam giác ABC có AB = c, AC = b, BC = a.
Tính độ dài cạnh b và độ dài đường trung tuyến ma biết a = 5 cm, c = 4 cm và .
Chứng minh rằng: với R là bán kính đường tròn ngoại tiếp tam giác ABC.
Câu 4. (2,5 điểm) Cho tam giác ABC có A(-2;3), B(1;4), C(0;-1)
Lập phương trình tham số cạnh AB.
Lập phương trình đường trung tuyến đi qua đỉnh A của tam giác ABC.
Tìm tọa độ điểm D thuộc trục Oy sao cho tam giác ABD vuông tại A.
Câu 5. (1 điểm)
Giải bất phương trình: 
Chứng minh rằng: với .
--------------Hết--------------
V . ĐÁP ÁN – THANG ĐIỂM
Câu
Ý
Nội dung
Điểm
1.
Giải các bất phương trình
3.0
a.
1,0
b.
1,0
c.
0,5
0,5
2.
Cho biểu thức 
2.0
1.
Để phương trình có hai nghiệm phân biệt thì 
1,0
2.
TH1: Với m = 1, ta có (không t/m )
Vậy m =1 không t/m.
TH2: Với thì 
0,25
0,25
0,5
3.
Hệ thức lượng trong tam giác
1.5
1.
Ta có 
0,5
0,5
2.
 (đpcm).
0,5
4.
Phương trình đường thẳng
2.5
1.
Đường thẳng AB đi qua A(-2;3), có vtcp là 
Pt tham số AB: 
1,0
2.
Gọi M là trung điểm BC 
Đường trung tuyến AM đi qua A, có vtcp là hay pt AM: 
0,25
0,25
0,5
3.
Vì D thuộc trục Oy nên giả sử D(0;b)
Ta có 
Để tam giác ABD vuông tại A thì 
Vậy D(0;-3).
0,25
0,25
0,25
0,25
5.
1.0
1.
Điều kiện: 
Kết hợp điều kiện ta được nghiệm bpt là .
0,25
0,25
2.
Đặt (đk: )
Ta có 
Dấu bằng xảy ra (vô lý)
Vậy với .
0,25
0,25
Tổng
10.0