Đề kiểm tra 45 phút – chương II Hình học 7 Trường THCS Nhơn Mỹ

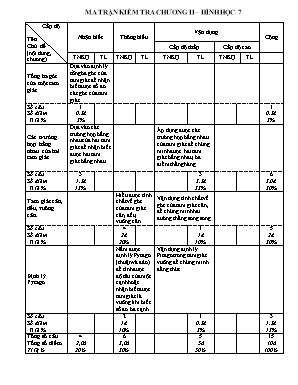
MA TRẬN KIỂM TRA CHƯƠNG II – HÌNH HỌC 7
 Cấp độ
Tên 
Chủ đề 
(nội dung,
chương)
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Tổng ba góc của một tam giác
Dựa vào định lý tổng ba góc của tam giác để nhận biết được số đo các góc của tam giác.
Số câu 
Số điểm 
 Tỉ lệ %
1
0,5đ 
5%
1
0,5đ 
5% 
Các trường hợp bằng nhau của hai tam giác
Dựa vào các trường hợp bằng nhau của hai tam giác để nhận biết được hai tam giác bằng nhau.
Áp dụng được các trường hợp bằng nhau của tam giác để chứng minh được hai tam giác bằng nhau, ba điểm thẳng hàng.
Số câu 
Số điểm 
 Tỉ lệ %
3
1,5đ 
15%
3
3,5đ 
35%
6
5,0đ
50%
Tam giác cân, đều, vuông cân. 
Hiểu được tính chất về góc của tam giác cân, đều, vuông cân.
Vận dụng tính chất về góc của tam giác cân, để chứng minh hai đường thẳng song song
.
Số câu 
Số điểm 
 Tỉ lệ %
4
2đ 
20%
1
1đ 
10%
5
2đ
30%
Định lý Pytago
Nắm được định lý Pytago (thuận và đảo) để tính được độ dài của một cạnh hoặc nhận biết được tam giác là vuông khi biết số đo ba cạnh. 
Vận dụng định lý Pitago trong tam giác vuông để chứng minh đẳng thức
Số câu 
Số điểm 
 Tỉ lệ %
2
1đ 
10%
1
0,5đ 
5%
3
1,5đ 
15%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
4
2,0đ 
20%
6
3,0đ 
30%
5
5đ
50%
15
10đ 100%
Trường THCS Nhơn Mỹ
Họ tên học sinh: ...
Lớp: ..
Thứ  ngày  tháng  năm 2016
Đề kiểm tra 45 phút – chương II.
Hình học 7
ĐIỂM
I. Trắc nghiệm: (5 điểm).
Câu 1. Tam giác ABC có , góc ngoài tại đỉnh A là 1300 thì số đo của góc B bằng:
Câu 2. HIK vuông tại H có các cạnh góc vuông là 3cm; 4cm. Độ dài cạnh huyền IK bằng:
Câu 3. Cho tam giác đều ABC. Vẽ các điểm M, N sao cho B là trung điểm của CM, C là trung điểm của BN. Số đo góc MAN bằng bao nhiêu?
Câu 4. Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC vẽ tam giác đều ABM. Số đo góc MCB là: 	
Câu 5. và có , . Thêm điều kiện nào sau đây để 
Câu 6. có thì :
	cân tại M	cân tại N	cân tại P	vuông tại N
Câu 7. Trong các tam giác có các kích thước sau đây, tam giác nào là tam giác vuông? 
Câu 8. Mỗi câu sau đúng hay sai? 
Câu
Nội dung
Đúng
Sai
A
Tam giác cân có một góc bằng là tam giác đều.
B
Nếu một tam giác vuông có một góc nhọn bằng thì tam giác đó là tam giác vuông cân
Câu 9. Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng.
Câu 10. Cho góc aOb. Trên cạnh Oa lấy điểm M, trên cạnh Ob lấy điểm N sao cho OM = ON. Vẽ tia phân giác Oc của góc aOb. Lấy điểm I thuộc Oc. Đường thẳng MN cắt Oc tại điểm H. Điền vào chỗ trống:
II. Tự luận: (5 điểm). Cho tam giác ABC cân ở A có Vẽ , . Gọi I là giao điểm của BD và CE.
 Chứng minh rằng: 
 Chứng minh rằng: AI là tia phân giác của góc BAC.
Chứng minh rằng: 
 Gọi M là trung điểm cạnh BC. Chứng minh ba điểm A, I, M thẳng hàng.
 Chứng minh: 
ĐÁP ÁN.
I. Trắc nghiệm: (5 điểm).
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
II. Tự luận: (5 điểm). 
BÀI
NỘI DUNG
Hình vẽ
a)
b)
c)
 cân tại A.
 cân tại A.
Từ (1) và (2): 
Vậy: (hai góc đồng vị bằng nhau)
d)
 là tia phân giác của góc BAC (3)
 là tia phân giác của góc BAC (4)
Từ (3) và (4): Ba điểm A, I, M thẳng hàng
e)
Ta có: vuông tại E.
Nên: (Định lý Pitago)
và: vuông tại E.
Nên: (Định lý Pitago)
, 
Nên: