Đề đề xuất kiểm tra chất lượng học kì II môn: Toán – lớp 9 (Đề 6)

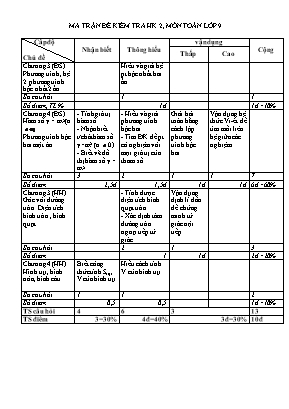
MA TRẬN ĐỀ KIỂM TRA HK 2, MÔN TOÁN LỚP 9 
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
vận dụng
Cộng
Thấp
Cao
Chương 3 (ĐS)
Phương trình, hệ 2 phương trình bậc nhất 2 ẩn.
Hiểu và giải hệ pt bậc nhất hai ẩn.
Sô câu hỏi
1
1
Số điểm, TL %
1đ
1đ=10%
Chương 4 (ĐS)
Hàm số y = ax2(a 
Phương trình bậc hai một ân.
- Tính giá trị hàm số 
- Nhận biết t/chât hàm số y=ax2 (a 0).
- Biết vẽ đồ thị hàm số y = ax2
- Hiểu và giải phương trình bậc hai.
- Tìm ĐK để pt có nghiệm với mọi giá trị của tham số.
Giải bải toán bằng cách lập phương trình bậc hai
Vận dụng hệ thức Vi-ét để tìm mối liên hệ giữa các nghiệm.
Sô câu hỏi
3
2
1
1
7
Số điểm
2,5đ
1,5đ
1đ
1đ
6đ=60%
Chương 3 (HH)
Góc với đường tròn. Diện tích hình tròn , hình quạt
- Tính được diện tích hình quạt tròn.
- Xác định tâm đường tròn ngoại tiếp tứ giác.
Vận dụng định lí đảo để chứng minh tứ giác nội tiếp.
Sô câu hỏi
2
1
3
Số điểm
1
1đ
2đ=20%
Chương 4 (HH)
Hình trụ, hình nón, hình câu.
Biết công thức tính Sxq, V của hình trụ
Hiểu cách tính V của hình trụ
Sô câu hỏi
1
1
2
Số điểm
0,5
0,5
1đ=10%
TS câu hỏi
4
6
3
13
TS điêm
3=30%
4đ=40%
3đ=30%
10đ 
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
 THÁP MƯỜI
KIỂM TRA CHẤT LƯỢNG HỌC KÌ II
Năm học: 2014 - 2015
Môn thi: TOÁN – Lớp 9
Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ ĐỀ XUẤT
(Đề gồm có một trang)
Câu 1 (1 điểm)
Giải hệ phương trình: 
Câu 2: (2,5 điểm)
Cho hàm số 
a) Tính : 
b) Khi x < 0, hàm số đã cho đồng biến hay nghịch biến? Vì sao?
c) Vẽ đồ thị hàm số 
Câu 3: (2,5 điểm)
Cho phương trình (ẩn x): (1)
a) Giải phương trình (1) khi m = 2.
b) Với giá trị nào của m thì phương trình (1) có nghiệm.
c) Tìm m để phương trình (1) có hai nghiệm thỏa mãn hệ thức: 
Câu 4: (1 điểm)
Một xe máy khởi hành từ thành phố A đi thành phố B dài 100 km. Cùng lúc đó, một ô tô cùng xuất từ thành phố A đi thành phố B với vận tốc lớn hơn vận tốc xe máy 10 km/h nên ô tô đã đến thành phố B trước xe máy 30 phút. Tính vận tốc mỗi xe.
Câu 5: (2 điểm)
Cho tam giác ABC nhọn. Hai đường cao BD và CK cắt nhau tại H.
Chứng minh tứ giác AKHD nội tiếp. Xác định tâm O đường tròn ngoại tiếp tứ giác AKHD.
Biết AH = 4 cm, . Tính diện tích hình quạt giới hạn bởi OD, OK và cung nhỏ DHK theo . 
Câu 6: (1 điểm)
Cho hình trụ có bán kính đáy r, chiều cao h.
a/ Viết công thức tính diện tích xung quanh, công thức tính thể tích của hình trụ.
b/ Tính thể tích hình trụ, biết bán kính đáy 5cm và chiều cao là 10cm.
Hết./.
CÂU
ĐÁP ÁN
BIỂU ĐIỂM
1
Vậy nghiệm của hệ phương trình (x ; y) = (3 ; 1)
0,25- 0,25-0,25
0,25
2
a) 
b) Khi x 0
c) 
x
-2
-1
0
1
2
y = x2
8
2
0
2
8
0,5
0,5
0,25 - 0,25
Lập bảng đúng 0,5
Vẽ đúng đồ thị 0,5
3
a) Thay m = 2 vào phương trình (1), ta được: 
a = 1, b = - 6, c = 5
Ta có : a + b + c = 1 - 6 + 5 = 0
Phương trình (1) có 2 nghiệm 
b) a = 1, b = - 6, c = 2m + 1
 b' = -3
 = 9 - 1(2m + 1)
 = - 2m + 8
Để phương trình (1) có nghiệm 
c) Với 
Ta có: 
Ta có : 
 (thỏa )
Vậy thì 
0,25
0,25
0,5
0,25 
0,25
0,25
0,25
0,25
0,25
4
Goi x (km/h) là vận tốc xe máy (x > 0)
Vận tốc ô tô: x + 10 (km/h)
Thời gian xe máy đi từ A đến B : (h)
Thời gian ô tô đi từ A đến B : (h)
30 phút = (h)
Theo đề bài ta có phương trình: 
Giải phương trình, ta được: ( nhận)
 (loại)
Vậy vận tốc xe máy 40 km/h, vận tốc ô tô 50 km/h.
0,25
0,25
0,25
0,25
5
a) Ta có: 
Vậy tứ giác ADHK nội tiếp đường tròn
- Đường tròn ngoại tiếp tứ ADHK có AH là đường kính nên tâm O đường tròn ngoại tiếp tứ giác ADHK là trung điểm AH.
b) Bán kính đường tròn ngoại tiếp tứ giác ADHK
Ta có: cm.
 sđ 
Diện tích hình quạt giới hạn bởi OD, OK và cung DHK
 (cm2)
0,5
0,25
0,25
0,5
0.25
0,25
6
a)
b)
 cm3
0,25
0,25
0,25
0,25
Chú ý: 
Học sinh có lời giải khác đúng cho điểm tối đa.
Riêng câu 5 không vẽ hình hoặc hình vẽ sai không chấm.