Đề 8 thi thử kỳ thi thpt quốc gia môn : Toán thời gian làm bài 180 phút

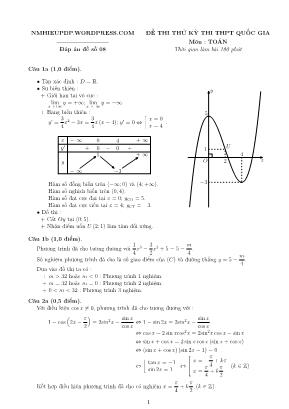
NMHIEUPDP.WORDPRESS.COM ĐỀ THI THỬ KỲ THI THPT QUỐC GIA
———————— Mụn : TOÁN
Đỏp ỏn đề số 08 Thời gian làm bài 180 phỳt
————
Cõu 1a (1,0 điểm).
• Tập xỏc định : D = R.
• Sự biến thiờn :
+ Giới hạn tại vụ cực :
lim
x→+∞ y = +∞; limx→−∞ y = −∞.
+ Bảng biến thiờn :
y′ =
3
4
x2 − 3x = 3
4
x (x− 4); y′ = 0⇔
ủ
x = 0
x = 4
.
x − ∞ 0 4 + ∞
y′ + 0 − 0 +
y
− ∞
5
−3
+ ∞
Hàm số đồng biến trờn (−∞; 0) và (4; +∞).
Hàm số nghịch biến trờn (0; 4).
Hàm số đạt cực đại tại x = 0; yCĐ = 5.
Hàm số đạt cực tiểu tại x = 4; yCT = −3.
• Đồ thị :
+ Cắt Oy tại (0; 5).
+ Nhận điểm uốn U (2; 1) làm tõm đối xứng.
y
xO
5
1
−3
4
2
U
Cõu 1b (1,0 điểm).
Phương trỡnh đó cho tương đương với
1
4
x3 − 3
2
x2 + 5 = 5− m
4
.
Số nghiệm phương trỡnh đó cho là số giao điểm của (C) và đường thẳng y = 5− m
4
.
Dựa vào đồ thị ta cú :
+ m > 32 hoặc m < 0 : Phương trỡnh 1 nghiệm.
+ m = 32 hoặc m = 0 : Phương trỡnh 2 nghiệm.
+ 0 < m < 32 : Phương trỡnh 3 nghiệm.
Cõu 2a (0,5 điểm).
Với điều kiện cosx 6= 0, phương trỡnh đó cho tương đương với :
1− cos
Å
2x− pi
2
ó
= 2sin2x− sinx
cosx
⇔ 1− sin 2x = 2sin2x− sinx
cosx
⇔ cosx− 2 sinxcos2x = 2sin2x cosx− sinx
⇔ sinx+ cosx = 2 sin x cosx (sinx+ cosx)
⇔ (sinx+ cosx) (sin 2x− 1) = 0
⇔
ủ
tanx = −1
sin 2x = 1
⇔
 x = −
pi
4
+ kpi
x =
pi
4
+ k
pi
2
(k ∈ Z)
Kết hợp điều kiện phương trỡnh đó cho cú nghiệm x =
pi
4
+ k
pi
2
, (k ∈ Z).
1
Cõu 2b (0,5 điểm).
Gọi z = a+ bi (a, b ∈ R), ta cú :đ |z|2 + 2z.z + |z|2 = 8
z + z = 2
⇔
đ
a2 + b2 + 2 (a2 + b2) + a2 + b2 = 8
2a = 2
⇔
đ
a2 + b2 = 2
a = 1
⇔
đ
b = ±1
a = 1
Vậy z = 1 + i hoặc z = 1− i.
Cõu 3 (0,5 điểm).
Với điều kiện x 6= 1, x > −1
2
, phương trỡnh đó cho tương đương với :
2(x− 1)2 − (2x+ 1) = log(2x+ 1)− log Ä2(x− 1)2ọ
⇔2(x− 1)2 + log Ä2(x− 1)2ọ = 2x+ 1 + log(2x+ 1) (1)
Xột hàm số f(t) = t+ log t trờn (0; +∞) cú f ′(t) = 1 + 1
t ln 10
> 0,∀t > 0.
Do đú (1)⇔ f(2(x− 1)2) = f(2x+ 1)⇔ 2(x− 1)2 = 2x+ 1⇔ x = 3±
√
7
2
(thỏa món).
Vậy phương trỡnh cú nghiệm x =
3±√7
2
.
Cõu 4 (1,0 điểm).
Xột hệ
2y3 + y + 2x
√
1− x = 3√1− x (1)√
9− 4y2 = 2x2 + 6y2 − 7 (2) .
Điều kiện x 6 1, −3
2
6 x 6 3
2
. Ta cú :
(1)⇔ 2y3 + y = 2Ä√1− xọ3 +√1− x
⇔ 2 Äy −√1− xọ Äy2 + y√1− x+ 1− xọ+ y −√1− x = 0
⇔ Äy −√1− xọ Ä2y2 + 2y√1− x+ 2(1− x) + 1ọ = 0
⇔
[
y =
√
1− xÄ
y +
√
1− xọ2 + y2 + 2− x = 0 (vụ nghiệm)
Với y =
√
1− x thay vào (2) được :
√
4x+ 5 = 2x2 − 6x− 1⇔ 2√4x+ 5 = 4x2 − 12x− 2⇔ Ä√4x+ 5 + 1ọ2 = 4(x− 1)2
Lấy căn bậc hai hai vế ta cú :
√
4x+ 5 + 1 = 2 (1− x)⇔ √4x+ 5 = 1− 2x⇔

x 6 1
2[
x = 1 +
√
2 (loại)
x = 1−√2
⇒ y = 4
√
2
Vậy hệ cú nghiệm duy nhất (x; y) =
Ä
1−√2; 4√2ọ.
Cõu 5 (1,0 điểm).
Thể tớch khối trũn xoay cần tỡm là V = pi
1∫
0
x2exdx.
Đặt
u = x2dv = exdx ⇒
du = 2xdxv = ex , ta cú :
2
V = pix2ex
∣∣∣1
0
− pi
1∫
0
2xexdx = pie− 2pi
1∫
0
xexdx
Lại đặt
u = xdv = exdx ⇒
du = dxv = ex , ta cú :
V = pie− 2pixex|10 + 2pi
1∫
0
exdx = −pie+ 2piex|10 = pi (e− 2)
Vậy V = pi(e− 2).
Cõu 6 (1,0 điểm).
Gọi H là hỡnh chiếu của S trờn AC, ta cú SH⊥(ABC).
Tam giỏc SAC vuụng tại S nờn SC =
√
AC2 − SA2 = a√3.
Từ đú suy ra đường cao SH =
SA.SC
AC
=
a
√
3
2
.
Tam giỏc ABC cõn tại B cú AC = 2a⇒ AB = BC = a√2.
Do đú diện tớch đỏy ABC là S∆ABC =
1
2
AB.BC = a2.
Vậy thể tớch khối chúp là VS.ABC =
1
3
S∆ABC .SH =
a3
√
3
6
.
A
B
C
S
K
H M
Gọi K là hỡnh chiếu của H trờn AB, ta cú
AB⊥HKAB⊥SH ⇒ AB⊥(SHK).
Gọi M là hỡnh chiếu của H trờn SK, ta cú
HM⊥SKHM⊥AB ⇒ HM⊥(SAB).
Do đú khoảng cỏch từ H đến (SAB) là d(H, (SAB)) = HM .
Trong tam giỏc SHA vuụng tại H cú HA =
√
SA2 − SH2 = a
2
⇒ CA = 4HA.
Tam giỏc AHK vuụng cõn tại K nờn ta cú HK =
HA√
2
=
a
2
√
2
.
Từ đú ta cú d(C, (SAB)) = 4d(H, (SAB)) = 4HM = 4
HS.HK√
HS2 +HK2
=
2a
√
21
7
.
Cõu 7 (1,0 điểm).
Gọi H ′ là giao điểm của AH và đường trũn ngoại tiếp tam giỏc ABC.
Ta cú ◊BAH ′ = ◊BCH ′ (vỡ cựng chắn cung B˘H ′).
Lại cú ◊BAH ′ = ữBCH (vỡ cựng phụ với 2 gúc đối đỉnh).
Từ đú suy ra ◊BCH ′ = ữBCH, hơn nữa HH ′⊥BC nờn H ′ đối xứng với H qua BC.
Đường thẳng HH ′ qua H(5; 5) và vuụng gúc BC nờn cú phương trỡnh x− y = 0.
Gọi K = HH ′ ∩BC thỡ tọa độ K là nghiệm hệ
x− y = 0x+ y − 8 = 0 ⇔
x = 4y = 4 ⇒ K(4; 4).
Vỡ K là trung điểm HH ′ nờn ta cú ⇒ H ′(3; 3).
Giả sử (ABC) : x2 + y2 − 2ax− 2by + c = 0 (a2 + b2 > c).
Vỡ M,N,H ′ ∈ (ABC) nờn ta cú :
49 + 9− 18a− 6b+ c = 0
16 + 4− 8a− 4b+ c = 0
9 + 9− 6a− 6b+ c = 0
⇔

a = 5
b = 4
c = 36
⇒ (ABC) : x2 + y2 − 10x− 8y + 36 = 0
3
Ta cú A là giao điểm khỏc H ′ của HH ′ và (ABC) nờn tọa độ A là nghiệm hệ :x− y = 0x2 + y2 − 10x− 8y + 36 = 0 ⇔
ủ
x = y = 3 (loại)
x = y = 6
⇒ A (6; 6)
Khi đú ta cú AH = d (A,BC) =
|6 + 6− 8|√
2
= 2
√
2.
Tọa độ B,C là nghiệm của hệx+ y − 8 = 0x2 + y2 − 10x− 8y + 36 = 0 ⇔
ủ
(x; y) = (3; 5)
(x; y) = (6; 2)
⇒ BC = 3
√
2
.
Vậy diện tớch tam giỏc ABC là S∆ABC =
1
2
AH.BC =
1
2
2
√
2.3
√
2 = 6.
Cõu 8 (1,0 điểm).
Đường thẳng ∆1 cú phương trỡnh tham số

x = 5 + 2t1
y = −t1
z = 4 + 2t1
.
Mặt phẳng (P ) cú vectơ phỏp tuyến −→n = (1; 1;−1).
Ta cú M ∈ ∆1 ⇒M(5 + 2t1;−t1; 4 + 2t1), N ∈ ∆2 ⇒ N(2− t;−1 + t;−5 + 3t).
Từ đú suy ra
−−→
MN(−2t1 − t− 3; t1 + t− 1;−2t1 + 3t− 9).
Và
[−−→
MN,−→n
]
= (t1 − 4t+ 10;−4t1 + 2t− 12;−3t1 − 2t− 2).
Vỡ MN⊥(P ) nờn
[−−→
MN,−→n
]
=
−→
0 ⇔

t1 − 4t+ 10
−4t1 + 2t− 12
−3t1 − 2t− 2
⇔
đ
t1 = −2
t = 2
.
Vậy M(1; 2; 0) và N(0; 1; 1).
Cõu 9 (0,5 điểm).
Chọn ngẫu nhiờn 4 học sinh trong 33 học sinh nờn số phần tử khụng gian mẫu là C433 = 40920.
Gọi A là biến cố "4 học sinh được chọn cú đủ học sinh giỏi, khỏ và trung bỡnh".
Chọn 4 học sinh cú đủ học sinh giỏi, khỏ và trung bỡnh cú cỏc trường hợp sau :
TH1 : Chọn 2 học sinh giỏi, 1 học sinh khỏ, 1 học sinh trung bỡnh cú C210.C
1
11.C
1
12 = 5940.
TH2 : Chọn 2 học sinh giỏi, 1 học sinh khỏ, 1 học sinh trung bỡnh cú C110.C
2
11.C
1
12 = 6600.
TH3 : Chọn 2 học sinh giỏi, 1 học sinh khỏ, 1 học sinh trung bỡnh cú C110.C
1
11.C
2
12 = 7260.
Từ đú ta cú |ΩA| = 5940 + 6600 + 7260 = 19800.
Vậy xỏc suất của biến cố A là P (A) =
|ΩA|
|Ω| =
19800
40920
=
15
31
.
Cõu 10 (1,0 điểm).
Áp dụng bất đẳng thức AM −GM ta cú

x√
y
+
x√
y
+ xy > 3x (1)
y√
x
+
y√
z
+ yz > 3y (2)
z√
x
+
z√
x
+ zx > 3z (3)
.
Cộng theo vế (1), (2) và (3) được 2
(
x√
y
+
y√
z
+
z√
x
)
+ xy + yz + zx > 3(x+ y + z) (∗).
Lại cú xy + yz + zx 6 x2 + y2 + z2 = (x+ y + z)2 − 2 (xy + yz + zx)⇔ xy + yz + zx 6 3.
Do đú (∗)⇔ 2
(
x√
y
+
y√
z
+
z√
x
)
> 3(x+ y + z)− 3⇔ x√
y
+
y√
z
+
z√
x
> 3 (đpcm).
——— Hết ———
4