Đề 6 thi thử kỳ thi thpt quốc gia môn : Toán thời gian làm bài 180 phút

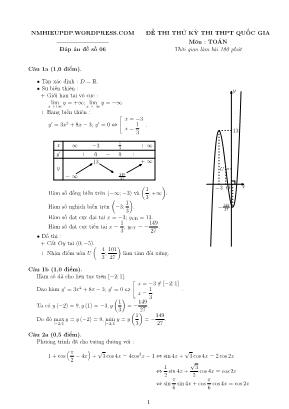
NMHIEUPDP.WORDPRESS.COM ĐỀ THI THỬ KỲ THI THPT QUỐC GIA
———————— Mụn : TOÁN
Đỏp ỏn đề số 06 Thời gian làm bài 180 phỳt
————
Cõu 1a (1,0 điểm).
• Tập xỏc định : D = R.
• Sự biến thiờn :
+ Giới hạn tại vụ cực :
lim
x→+∞ y = +∞; limx→−∞ y = −∞.
+ Bảng biến thiờn :
y′ = 3x2 + 8x− 3; y′ = 0⇔
 x = −3
x =
1
3
.
x − ∞ −3 13 + ∞
y′ + 0 − 0 +
y
− ∞
13
−149
27
+ ∞
Hàm số đồng biến trờn (−∞;−3) và
ầ
1
3
; +∞
ồ
.
Hàm số nghịch biến trờn
ầ
−3; 1
3
ồ
.
Hàm số đạt cực đại tại x = −3; yCĐ = 13.
Hàm số đạt cực tiểu tại x =
1
3
; yCT = −149
27
.
• Đồ thị :
+ Cắt Oy tại (0;−5).
+ Nhận điểm uốn U
ầ
−4
3
;
101
27
ồ
làm tõm đối xứng.
y
xO
13
−149
27
−3
U
Cõu 1b (1,0 điểm).
Hàm số đó cho liờn tục trờn [−2; 1].
Đạo hàm y′ = 3x2 + 8x− 3; y′ = 0⇔
 x = −3 /∈ [−2; 1]
x =
1
3
.
Ta cú y (−2) = 9, y (1) = −3, y
ầ
1
3
ồ
= −149
27
.
Do đú max
[−2;1]
y = y (−2) = 9, min
[−2;1]
y = y
ầ
1
3
ồ
= −149
27
.
Cõu 2a (0,5 điểm).
Phương trỡnh đó cho tương đương với :
1 + cos
Åpi
2
− 4x
ó
+
√
3 cos 4x = 4cos2x− 1⇔ sin 4x+
√
3 cos 4x = 2 cos 2x
⇔ 1
2
sin 4x+
√
3
2
cos 4x = cos 2x
⇔ sin pi
6
sin 4x+ cos
pi
6
cos 4x = cos 2x
1
⇔ cos
Å
4x− pi
6
ó
= cos 2x
⇔
 x =
pi
36
+ k
pi
3
x =
pi
12
+ kpi
(k ∈ Z)
Vậy phương trỡnh đó cho cú nghiệm x =
pi
12
+ kpi;x =
pi
36
+ k
pi
3
(k ∈ Z).
Cõu 2b (0,5 điểm).
Gọi z = a+ bi (a, b ∈ R)⇒ z = a− bi, ta cú :
|z − 1|2 − z = |a− bi− 1|2 − a− bi = (a− 1)2 + b2 − a− bi = a2 + b2 − 3a+ 1− bi
Theo giả thiết z.z = 2 và |z − 1|2 − z là số thuần ảo nờn ta cú hệ :đ
a2 + b2 = 2
a2 + b2 − 3a+ 1 = 0 ⇔
đ
b2 = 2− a2
−3a+ 3 = 0 ⇔
đ
b = ±1
a = 1
Vậy z = 1 + i hoặc z = 1− i.
Cõu 3 (0,5 điểm).
Bất phương trỡnh đó cho tương đương với :
34x
2−2x < 3−2x
2−x+1 ⇔ 4x2 − 2x < −2x2 − x+ 1⇔ −1
3
< x <
1
2
Vậy bất phương trỡnh đó cho cú tập nghiệm S =
ầ
−1
3
;
1
2
ồ
.
Cõu 4 (1,0 điểm).
Xột hệ phương trỡnh
8x3 + 2x = y3 + y (1)x2 − x+ 2 = y2 − y (2) .
Biến đổi phương trỡnh (1) ta cú :
(1)⇔ (2x)3 − y3 + 2x− y = 0⇔ (2x− y) Ä4x2 + 2xy + y2 + 1ọ = 0
⇔
ủ
y = 2x
(x+ y)2 + 3x2 + 1 = 0 (vụ nghiệm)
Với y = 2x thay vào (2) được x2 − x+ 2 = 4x2 − 2x⇔ 3x2 − x− 2 = 0⇔
 x = 1
x = −2
3
.
Vậy hệ cú hai nghiệm (x; y) = (1; 2) và (x; y) =
ầ
−2
3
;−4
3
ồ
.
Cõu 5 (1,0 điểm).
Đặt u = lnx⇒ du = 1
x
dx.
Đổi cận x = 1⇒ u = 0;x = e⇒ u = 1, ta cú :
I =
1∫
0
u− 2
u+ 1
du =
1∫
0
ầ
1− 3
u+ 1
ồ
du = (u− 3 ln |u+ 1|)|10 = 1− 3 ln 2
Vậy I = 1− 3 ln 2.
2
Cõu 6 (1,0 điểm).
Tam giỏc SAB vuụng tại S nờn SB =
√
AB2 − SA2 = a
√
3
2
.
Vỡ SB là hỡnh chiếu của AB trờn (SBC) và BC⊥SA nờn BC⊥SB.
Suy ra diện tớch tam giỏc SBC là S∆SBC =
1
2
SB.BC =
a
√
3
2
.a
√
3 =
3a2
2
.
Do đú thể tớch khối chúp S.ABC là VS.ABC =
1
3
SA.S∆SBC =
1
3
a
2
3a2
2
=
a3
4
.
A
B
CS
I
M
N
K
Gọi M,N, I,K lần lượt là trung điểm của SA,AC, SB, SC.
Khi đú MN ||SC,MI||AB nờn gúc giữa SC và AB bằng gúc giữa MN và MI.
Ta cú MN =
1
2
SC =
a
√
15
2
;MI =
1
2
AB =
a
2
; IK =
1
2
BC =
a
√
3
2
.
Và NK||SA⇒ NK⊥(SBC)⇒ NK⊥KI ⇒ NI = √NK2 +KI2 = 7a
4
.
Do đú trong tam giỏc MNI cú cos ữMNI = MN2 +MI2 −NI2
2MN.MI
=
√
15
8
> 0.
Vậy cos(SC,AB) = cos(MN,MI) =
√
15
8
.
Cõu 7 (1,0 điểm).
Gọi I là tõm hỡnh thoi và G = BM ∩ AC ⇒ G là trọng tõm ∆BCD.
Trong tam giỏc vuụng BIG ta cú sin ’BIG = IG
BG
=
IG√
BI2 + IG2
=
IGằ
(6IG)2 + IG2
=
1√
37
.
Khi đú cos (BD,AH) = sin ’BIG = 1√
37
.
Gọi vectơ phỏp tuyến của AH là −→n = (a; b) 6= −→0 .
Ta cú cos (BD,AH) =
1√
37
⇔ |a− b|√
a2 + b2.
√
2
=
1√
37
⇔ 35a2− 74ab+ 35b2 = 0⇔
ủ
5a = 7b
7a = 5b
.
Với 5a = 7b, chọn −→n = (7; 5) ta cú phương trỡnh AH là 7(x−2)+5(y+1) = 0⇔ 7x+5y−9 = 0.
Với 7a = 5b, chọn −→n = (5; 7) ta cú phương trỡnh AH là 5(x−2)+7(y+1) = 0⇔ 5x+7y−3 = 0.
Vậy AH : 7x+ 5y − 9 = 0 hoặc AH : 5x+ 7y − 3 = 0.
Cõu 8 (1,0 điểm).
Đường thẳng d1 qua M1(0; 3;−1) và cú vộctơ chỉ phương −→u1 = (−1; 2; 3).
Đường thẳng d2 qua M2(4; 0; 3) và cú vộctơ chỉ phương
−→u2 = (1; 1; 2).
Ta cú [−→u1,−→u2] = (1; 5;−3) ,−−−−→M1M2 = (4;−3; 4)⇒ [−→u1,−→u2] .−−−−→M1M2 = 4− 15− 12 = −23 6= 0.
Do đú d1 và d2 chộo nhau (đpcm).
3
Tọa độ giao điểm A của d1 và (P ) là nghiệm hệ 4x− 3y + 11z − 26 = 0x−1 = y − 32 = z + 13 ⇔

x = −2
y = 7
z = 5
⇒ A (−2; 7; 5)
Tọa độ giao điểm B của d2 và (P ) là nghiệm hệ 4x− 3y + 11z − 26 = 0x− 4
1
=
y
1
=
z − 3
2
⇔

x = 3
y = −1
z = 1
⇒ B (3;−1; 1)
Vỡ ∆ ⊂ (P ) và cắt d1, d2 nờn qua A,B, do đú nhận −→AB = (5;−8;−4) làm vộctơ chỉ phương.
Vậy ∆ cú phương trỡnh
x+ 2
5
=
y − 7
−8 =
z − 5
−4 .
Cõu 9 (0,5 điểm).
Mỗi đề thi gồm 5 cõu chọn từ tổng số 30 cõu nờn ta cú |Ω| = C530 = 142506.
Gọi A là biến cố đề thi lấy ra là một đề thi "Tốt".
Vỡ một đề thi "Tốt" gồm ba loại cõu dễ, trung bỡnh và khú, đồng thời số cõu dễ khụng ớt hơn
2 nờn cú 3 trường hợp sau thuận lợi cho biến cố A :
TH1 : Đề gồm 3 cõu dễ, 1 cõu trung bỡnh và 1 cõu khú. Trường hợp này cú C315.C
1
10.C
1
5 đề.
TH2 : Đề gồm 2 cõu dễ, 2 cõu trung bỡnh và 1 cõu khú. Trường hợp này cú C2C210.C
1
5 đề.
TH3 : Đề gồm 2 cõu dễ, 1 cõu trung bỡnh và 2 cõu khú. Trường hợp này cú C215.C
1
10.C
2
5 đề.
Từ đú suy ra |ΩA| = C315.C110.C15 + C215.C210.C15 + C215.C110.C25 = 56875.
Vậy xỏc suất để đề thi lấy ra là một đề thi "Tốt" là P (A) =
|ΩA|
|Ω| =
56875
142506
=
625
1566
.
Cõu 10 (1,0 điểm).
Trước hết ta chứng minh
1
1 + x2
+
1
1 + y2
6 2
1 + xy
đỳng với mọi x, y > 0 và xy 6 1.
Thật vậy
1
1 + x2
+
1
1 + y2
= 1 +
1− (xy)2
1 + x2 + y2 + (xy)2
6 1 + 1− (xy)
2
1 + 2xy + (xy)2
= 1 +
1− xy
1 + xy
=
2
1 + xy
Trường hợp 1: z > 1;xy 6 1, ta cú :ầ
1√
1 + x2
+
1√
1 + y2
ồ2
=
1
1 + x2
+
1
1 + y2
+
2ằ
1 + x2 + y2 + (xy)2
6 2
1 + xy
+
2
1 + xy
=
4
1 + xy
Hay
1√
1 + x2
+
1√
1 + y2
6 2√
1 + xy
.
Lại cú xyz = 1⇔ xy = 1
z
, suy ra
1√
1 + x2
+
1√
1 + y2
6 2 
1 +
1
z
=
2
√
z√
1 + z
.
Khi đú
P =
1√
1 + x2
+
1√
1 + y2
+
1√
1 + z
6 2
√
z + 1√
1 + z
=
√
4z + 4
√
z + 1
z + 1
=
Ã
5− (
√
z − 2)2
z + 1
6
√
5
Trường hợp 2: z 6 1;xy > 1, giả sử x > y ta cú x > 1 và yz 6 1, khi đú :
1√
1 + x2
+
1√
1 + y2
+
1√
1 + z
≤ 1√
1 + x
+
1√
1 + y2
+
1√
1 + z2
6
√
5 (do trường hợp 1)
Dấu bằng xảy ra khi x = y =
1
2
, z = 4. Vậy giỏ trị lớn nhất của P là
√
5.
——— Hết ———
4